対応のある・対応のない

統計学における用語である「対応のある」と「対応のない」とはどのような意味か解説します．

それぞれの場合のデータに用いることができる検定手法についても解説します．

対応のない場合

”対応のない”とは異なる個体に対して，それぞれの条件で測定したという意味になります．

例として，社会人の男性・女性ごとにアンケート調査した結果，得られたデータは対応のないデータとなります．個体の属性（人であれば年齢や性別など）による差を比較する際に用いるデータは，対応のないデータとなります．

もう1つ，対応のないデータの例として「年代ごとのワインに対する味覚調査」を説明します．

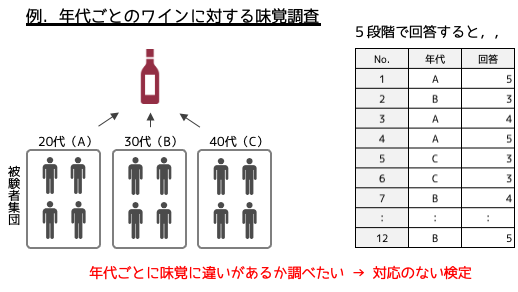
特定のワインに対する評価を年代ごとに分けたデータは，対応のないデータになります．対応のないデータは図表のようにロングデータ（縦持ちデータ）として整理されます．

対応のない場合の検定手法として，一般的に使われるのが対応のないｔ検定やウィルコクソンの順位和検定になります．ワインの例では年齢によって3つの群に分けたため，多重比較を行います．

対応のない場合の差の検定

対応のない場合の差の検定手法について紹介します．

検定手法	グループ数	データ	正規性	等分散性
カイ二乗検定	2以上	質的
フィッシャーの正確確率検定	2	質的
対応のないｔ検定	2	量的	○	○
ウェルチのｔ検定	2以上	量的	○
マンホイットニーのU検定	2	量的・順序		○
ブルンナー・ムンチェル検定	2	量的・順序
一元配置分散分析	3以上	量的	○	○
クラスカル・ウォリス検定	3以上	量的・順序
ボンフェローニ補正	3以上	量的・順序
スティール・ドゥワス検定	3以上	量的・順序		○

※ グループ数：扱うデータのグループ数．複数であれば2グループ以上のデータに対して検定を行えます．
※ データ：扱うことができるデータの種類です．➔ 統計学におけるデータの種類
※ 正規性：扱うデータの母集団が正規分布に仮定できるかです．

対応のないｔ検定とウェルチのｔ検定の違いは，等分散性になります．等分散性とは2つのグループの分散がおおよそ同じであるかです．等分散性を確認する方法としてF検定がありますが，近年は等分散性に疑いがある場合は，ウェルチのｔ検定を行うというのが主流です．

母集団を正規分布に仮定する必要が無い，カイ二乗検定やマンホイットニーのU検定（ウィルコクソンの順位和検定）はノンパラメトリック検定と呼ばれる手法になります．ノンパラメトリック検定については以下のページで解説しています．

》ノンパラメトリック検定

扱うデータのグループ数が3つ以上の場合は，分散分析やクラスカル・ウォリス検定，異なるグループを特定したい場合はスティール・ドゥワス検定を行います．

分散分析や多重比較については以下のページで解説しています．

》分散分析
》多重比較

対応のある場合

”対応のある”とは同一の個体に対して，それぞれの条件で測定したという意味になります．

社会人に5年前の年収と現在の年収を調査した結果，得られたデータは対応のあるデータとなります．時間経過やイベントの発生前後での差を比較する際に，用いるデータは対応のあるデータとなります．

別の例として，対応のあるデータの例として「ワインの飲み比べ調査」を説明します．

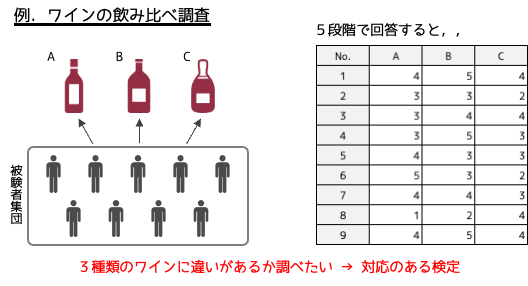
3種類のワインを同じ被験者集団が評価して得られたデータは，対応のあるデータになります．対応のあるデータは図表のようにワイドデータ（横持ちデータ）として整理されます．

対応のある場合の検定手法として一般的に使われるは，対応のあるｔ検定やウィルコクソンの符号順位検定になります．

対応のある場合の差の検定

対応のある場合の差の検定手法について紹介します．

検定手法	グループ数	データ	正規性
マクネマー検定	2	質的
対応のあるｔ検定	2	量的	○
マクネマー検定	2	質的
コクランのQ検定	3以上	質的
ウィルコクソンの符号順位検定	2	量的・順序
反復測定一元配置分散分析	3以上	量的	○
フリードマン検定	3以上	量的・順序
ボンフェローニ補正	3以上	量的・順序

※ グループ数：扱うデータのグループ数．複数であれば2グループ以上のデータに対して検定を行えます．
※ データ：扱うことができるデータの種類です．➔ 統計学におけるデータの種類
※ 正規性：扱うデータの母集団が正規分布に仮定できるかです．

対応のある場合のノンパラメトリック検定としてよく使われるのは，ウィルコクソンの符号順位検定になります．対応のある場合で紹介したウィルコクソンの順位和検定と名称は似ていますが，計算方法は違うため注意してください．

3つ以上のグループが対応のある場合に行うのがフリードマン検定になります．フリードマン検定はノンパラメトリック検定なので，データの母集団が正規分布に仮定できない場合にも行うことができます．