ウィルコクソンの符号順位検定とは
ウィルコクソンの符号順位検定とは,対応のある2群の差の検定(対応のあるt検定)のノンパラメトリック版です.順序尺度以上のデータに対して用いることができます.
ウィルコクソンの符号順位検定の考え方は以下になります.
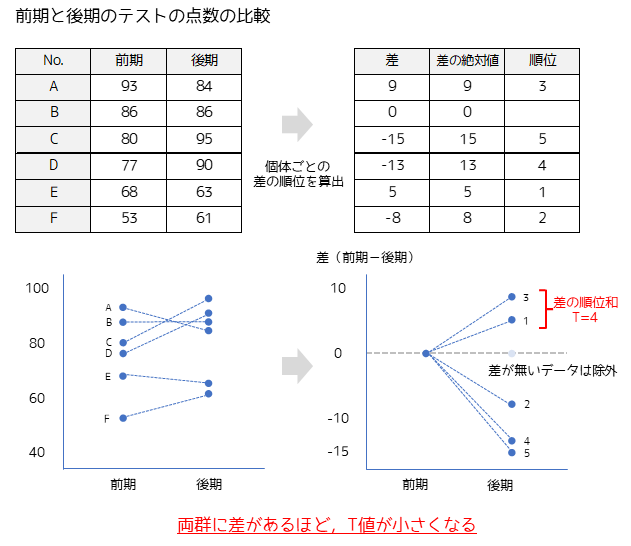
ウィルコクソンの符号順位検定では,2群のデータを個体ごとに差を計算してから差の絶対値の順位を求めます.差の符号ごとに順位の合計値(順位和)を算出して,小さい方がT値となります.
T値は両群に差があるほど小さい値(T値の分布の端)なり,限界値より小さい場合に差があると判定します.
小標本の場合はT値を検定統計量として,専用の検定表(サインランク表)から読み取った棄却値と比較します.小標本とはサンプルサイズが25以下の場合です.
大標本の場合はT値は近似的に正規分布に従うため,標準化したT値を検定統計量としたz検定を行います.
ウィルコクソンの符号順位検定の手順
ウィルコクソンの符号順位検定は以下の手順で行います.
① 仮説の設定
帰無仮説は「2群の母集団に差がない」,対立仮説は「2群の母集団に差がある」として設定します.
② 有意水準の決定
ウィルコクソンの符号順位検定では有意水準α=0.05,もしく0.01とします.
③ 検定統計量の算出
具体的な計算手順は,Excelを用いた方法で解説しています.
④ p値の算出
検定統計量からp値を算出します.小標本の場合は求めません.
⑤ 有意差判定
○大標本の場合
p値<0.05であれば,帰無仮説は棄却されて対立仮説を採択 → 「2群の母集団に差がある」
p値\(\geq\)0.05であれば,帰無仮説は棄却されない → 「2群の母集団に差があるとは言えない」
○小標本の場合
検定統計量<限界値であれば,帰無仮説は棄却されて対立仮説を採択
検定統計量\(\geq\)限界値であれば,帰無仮説は棄却されない
仮説検定の考え方や用語については,以下のページで解説しています.
検定結果を間違いたくない方へ
Excelを用いた計算方法より簡単・正確に,ウィルコクソンの符号順位検定の検定結果を調べることができる統計解析アプリStaatAppを販売しております.小標本の場合でもp値や効果量を簡単に求めることができます.
StaatAppではウィルコクソンの符号順位検定以外にも,様々なノンパラメトリック検定をクリックするだけで実行することができます.詳細は以下のページをお読みください.
》StaatAppで行う仮説検定
》統計解析アプリStaatApp
例題の設定
例題では以下のサンプルデータを用います.学生10人のある科目に対する前期と後期の点数になります.
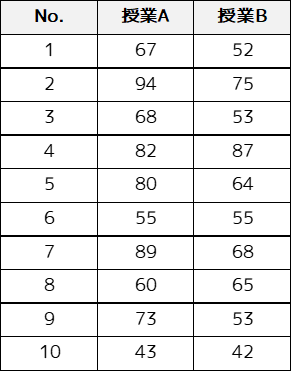
帰無仮説は「前期と後期でテストの点数に差がない」となり,対立仮説は「前期と後期でテストの点数に差がある」と設定します.
有意水準α=0.05で両側検定を行います.
Excelを用いたT値の計算手順
Excelを用いたT値の計算手順について説明します.
以下のような表を作成して,T値を求めます.
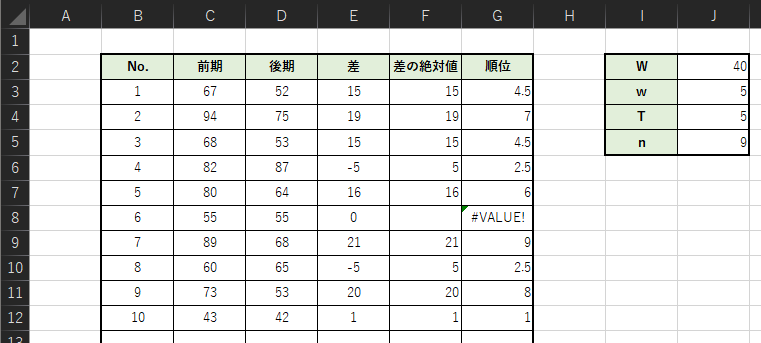
各セルの入力式は以下のようになります.
・E列:=C3-D3 ※3行目のセルの数式です.下の行へは数式のコピーを行ってください.
・F列:=IF(E3=0,””,ABS(E3))
・G列:=RANK.AVG(F3,F:F,1)
・J2:=SUMIF(E:E,”>0″,G:G)
・J3:=SUMIF(E:E,”<0″,G:G)
・J4:=MIN(J2,J3)
・J5:=COUNTIF(G:G,”>0″)
入力式と計算手順について解説します.
① データの入力【C列】【D列】
群(前期・後期)ごとに値(点数)を各1列にデータを入力します.
② 差を求める【E列】
個体(学生)ごとのデータの差を求めます.
③ 差の絶対値を求める【F列】
差の絶対値を求めます.差が無いデータはセルの値を空白にするために,IF関数と組み合わせて差の絶対値を求めます.
絶対値はABS関数を用いて求めることができます.
④ 差の絶対値の順位を求める【G列】
差の絶対値の順位を求めます.差がないデータは除いて順位を付けます.
順位データはRANK.AVG関数を用いて計算します.RANK.AVG関数の引数は以下になります.
RANK.AVG(“順位に変換する値”,”順位の対象となるデータ群(列)”,1)
※ 値が小さいほど順位が高くなるように計算します.
差の絶対値が空白の行は,”#VALUE!”が返ってきて問題ありません.
⑤ 符号ごとの合計順位を求める【J2】【J3】
②で求めた差の符号ごとに合計順位を求めます.(符号順位検定の特徴的な操作です)
「E列」が正の値の場合の順位和Wと,負の値の場合の順位和wを計算するためにSUMIFS関数を用います.SUMIFS関数の引数は以下になります.
SUMIFS(“合計する値の範囲(列)”,”合計するか判定する値の範囲(列)”,”判定する値の範囲と一致させる値”)
⑥ T値を求める【J4】
符号ごとの順位和Wとwのうち小さい方がT値になります.ExcelではMIN関数を用いて判定することができます.
例題では,W=40,w=5という値が計算できたのでT=5となります.
⑥ サンプルサイズを求める【J5】
サンプルサイズを求めます.差がないデータはサンプルサイズとしてカウントしません.
COUNTIFS関数を用いて,「G列」の値が0より大きいセルがいくつあるかカウントします.例題ではNo.6の大学生が同じ点数であったため,サンプルサイズは9になります.
小標本の有意差判定
小標本の場合はT値を検定統計量として,サインランク検定表から読み取った限界値と比較することで有意差があるか判定します.
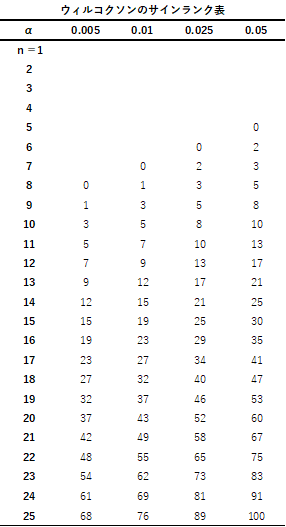
有意水準α=0.05,サンプルサイズn=9で両側検定の場合,α=0.05/2=0.025,n=9の値をサインランク表から読み取ります.
限界値が5で検定統計量T=5であるので,検定統計量=限界値となり有意差は見られないため帰無仮説は棄却されません.
例題の結論としては,「前期と後期でテストの点数に差があるとは言えない」となります.
大標本の有意差判定
大標本の場合はT値は近似的に正規分布に従うため,標準化したT値を検定統計量としたz検定を行います.
例題ではデータの個数が10でしたが,同じデータを用いて仮にデータの個数が26以上だった場合,どのような計算を行うか説明をします.
以下のようにT値の計算手順に追記して,標準化したT値zTとp値を求めます.
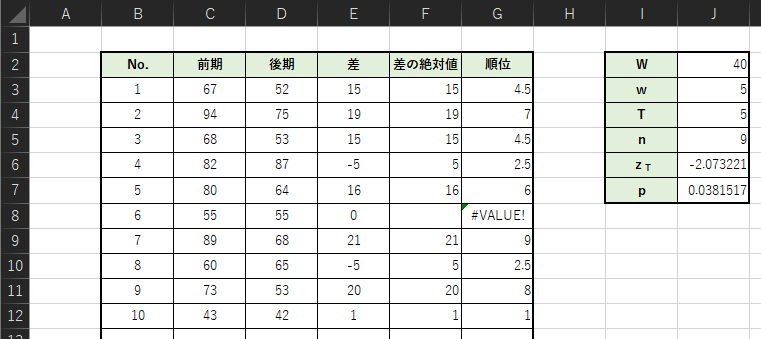
追加した入力式は以下のようになります.
・J6:=(J4-J5*(J5+1)/4)/(SQRT(J5*(J5+1)*(2*J5+1)/24))
・J7:=2*(1-NORM.S.DIST(ABS(J6),TRUE))
入力式と計算手順について解説します.
① 標準化したT値を求める【J6】
z検定での検定統計量であるzTを求めます.標準化したT値zTは以下の式を用いて求めます.
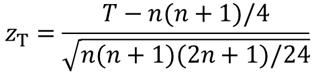
nは差が無い個体を除いたサンプルサイズです.
② p値を求める【J7】
検定統計量zTからNORMSDIST関数を用いてp値を求めます.
仮の計算例では,p値=0.0381..となります.p値<有意差α=0.05であるので帰無仮説は棄却され対立仮説が採択されます.
片側検定を行う場合は,以下の式を用いてp値を計算してください.
ex) 片側検定のp値の計算式:=1-NORM.S.DIST(ABS(J6),TRUE)
補足① ウィルコクソンのサインランク表
ウィルコクソンのサインランク表は以下になります.有意水準αの値は片側検定で用いる値になるので両側検定の場合は,有意水準α/2として限界値を見つけてください.
補足② 効果量の求め方(Excel版)
仮説検定の結果として重要な効果量の求め方について,Excelを用いて解説します.
ノンパラメトリック検定の効果量rは,以下の式で求めることができます.
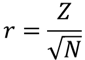
効果量と検定力分析入門 水本・竹内(2010)
※ 効果量には様々な計算方法があるため,論文などでは引用元もしくは計算式を示す必要があります.
例題では標準化した検定統計量Z=-2.073..でサンプルサイズN=10となり,効果量r=-0.655..となります.
効果量rの値の目安としては次のようになるので,比較した2群には統計学的に大きい差があると判断することができます.
【効果量rの目安】 小:0.1 中:0.3 大:0.5
補足③ データの前提条件
用いるデータの前提条件を解説します.
① ノンパラメトリックなデータ
ウィルコクソンの符号順位検定はノンパラメトリックな(=正規分布でない)データに対して行います.用いるデータが正規分布と仮定できる場合は対応のあるt検定を行います.
② 順序尺度
名義尺度のデータに対しては用いることができません.名義尺度はデータの大小に意味が無い,つまり順位和を求めることができないことから明らかです.名義尺度のデータの差や関連性を分析する際は,クロス集計表などを用います.
③ 対応のあるデータ
比較する2つのグループは対応のある場合(同一個体のデータ)である必要があります.対応のない場合は,マンホイットニーのU検定を行います.
検定方法の選び方は以下のページでまとめて紹介しています.









