効果量とは
効果量(Effect Size)とは仮説検定において,帰無仮説がどれだけ正しくないかを示す指標になります.効果量は要因が持つ本来の性質であり,サンプルサイズやデータの単位に依存しない指標となります.
統計学において効果量は,主に2つの用途で使われます.
① 検定結果の正しさを示す
② 検出力分析でサンプルサイズを決めるパラメータ
①について,仮説検定の結果を示す際に多くの人がp値もしくは有意差判定の結果のみを書きます.しかし,p値とはあくまでも「帰無仮説が正しいとした時に,検定統計量より稀な値が観測される確率」であり,比較した群間の差の大きさまでは分かりません.
検定の結果が同じp値であってもサンプルサイズが大きい場合は,僅かな差があるだけでp値を小さい値となります.
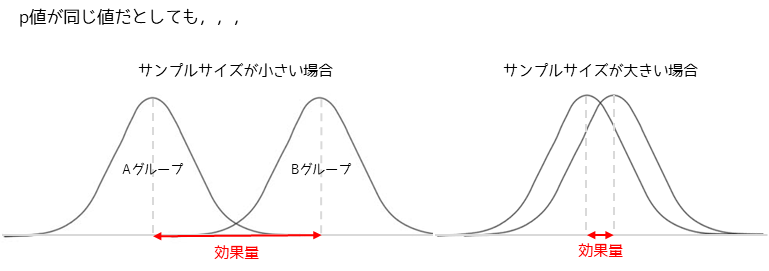
検定結果において差の大きさを示すために,効果量を用います.効果量の値が大きくなるほど,比較した群間の差が大きくなります.(同じp値の場合,サンプルサイズが小さい方が効果量を大きくなります)
論文で仮説検定の結果を示す際はp値に加えて,効果量も記載することを推奨します.
サンプルサイズが大きい(n=100など)と僅かな差でも有意差があると判定してしまいます.そこで適切なサンプルサイズを決めるのが検出力分析,効果量の②の使い方になります.
検出力分析については効果量とサンプルサイズの関係で詳しく解説していますが,検出力分析を行なう際のパラメータの1つとして効果量があります.
効果量は検定方法によって計算式が異なります.代表的な仮説検定である対応のないt検定の場合は,以下の式で求めることができます.

nは各群のサンプルサイズとなり,サンプルサイズに依存しない値として求められます.
対応のないt検定以外の効果量も全て検定統計量に対してサンプルサイズや自由度の影響を取り除くような計算式で求めることができます.
主な効果量の目安
分析方法によって効果量の定義は異なります.主な効果量と値の目安を紹介します.
rで示される効果量はr族と言い,関連の強さを示す効果量になります.dで示される効果量はd族と言い,差の大きさを示す効果量になります.
|
分析名
|
効果量の指標 | 効果量の目安 | ||
|
小
|
中
|
大
|
||
| 相関分析 | d | 0.1 | 0.3 | 0.5 |
| 重回帰分析 | R2 | 0.02 | 0.13 | 0.26 |
| t検定 | d | 0.2 | 0.5 | 0.8 |
| 一次元分散分析 | η2 | 0.01 | 0.06 | 0.14 |
| 多重比較 | r | 0.1 | 0.3 | 0.5 |
| カイ二乗検定 | 2×2の場合 φ 2×2以外 V |
0.1 | 0.3 | 0.5 |
| ノンパラメトリック検定 | r | 0.1 | 0.3 | 0.5 |
効果量の大きさはあくまでも目安で,研究分野によって変わるので論文に用いる際は既往研究を参考にしてください.ここで示してる目安は以下の論文から作成しています.
相関分析や重回帰分析ではそれぞれ相関係数r,決定係数R2が効果量となります.これらの値は分析結果として一般的に使われる統計量です.
2×2以外のクロス集計表ではクラメールの連関係数Vが効果量になります.クラメールの連関係数もクロス集計表の分析方法として一般的に使われる統計量になります.
ノンパラメトリック検定の効果量は,検定統計量をZ変換して求めることができます.
効果量の計算方法
効果量の求め方は同じ検定方法に対しても,複数の計算方法があります.
例えば対応のないt検定においては,既に紹介したd族の効果量(Choen’s d)の他にr族の効果量もあります.研究の結果として効果量を記載する際は,使用した計算式や引用論文も添えるようにしましょう.
各検定方法の効果量の求め方は,それぞれの詳細ページで解説しています.
効果量を算出するならStaatApp
統計アプリStaatAppを用いれば,様々な仮説検定の検定統計量やp値,効果量が簡単・正確に算出することができます.
t検定などのパラメトリック検定は無料で使用できるので,お気軽にダウンロードしてお使いください.
》StaatAppで行う仮説検定
》統計解析アプリStaatApp
効果量とサンプルサイズの関係
効果量は仮説検定における適切なサンプルサイズを求めるためのパラメータとしても利用されます.
検出力・効果量・有意水準・サンプルサイズには以下のような関係があります.
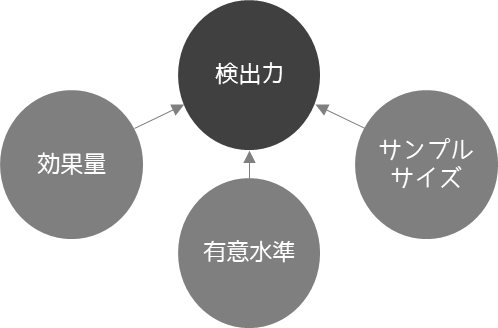
4つの要素の中で特定の1つの要素は,残りの3つの要素から計算することができます.適切なサンプルサイズは検出力と効果量,有意水準から求めることができます.
検出力とは仮説検定において,母集団が異なるときに帰無仮説を棄却する確率で第二種の過誤の確率βの補数(1-β)になります.
効果量と有意水準,サンプルサイズから検出力を求めることを検出力分析と言います.










