統計解析におけるグラフを用いる重要性や,様々な分布を表すグラフについて解説します.
分布を可視化するグラフ
統計解析ではデータの分布を調べる・示すためにグラフがよく用いられます.代表的なデータの分布を表すグラフとしてヒストグラム(度数分布図)や散布図があります.
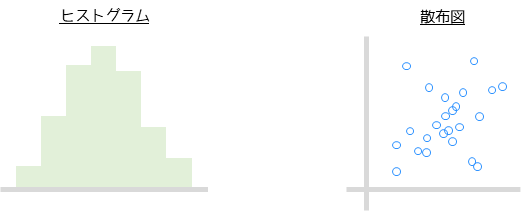
グラフを用いることでデータの傾向を視覚的に捉えることができます.また,統計解析の元データを効率的に示すことができます.
グラフを用いる重要性
統計学においてデータの特徴を示す基本統計量として,平均値や分散があります.分散はデータの散らばり具合を示す指標です.
以下のような平均値と分散が等しい2つのデータがあるとします.
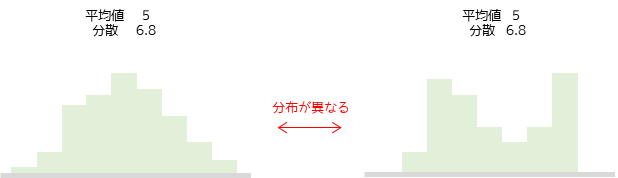
基本統計量のみで考えると2つのデータは同じ特徴を持つと考えることができます.しかし,ヒストグラムを用いてデータの分布を比較すると異なることがわかります.
基本統計量はデータの特徴を要約するため,データ分析に必要な情報まで失っている可能性がありますが,適切なグラフを用いることで情報をなるべく失うことなく,データの特徴を知らべることができます.
外れ値を検出できるのもグラフを利用する大きなメリットです.

グラフを作成することで,明らかにデータ群から外れている値(外れ値)を検出することができます.データ分析を行う際に外れ値を含めて分析を行うと,本来期待している結果とならないことが多いため,事前に外れ値の有無を調べることは非常に重要です.
様々な分布を表すグラフ
データの分布を示すグラフとして基本になるのが,ここまでも紹介しているヒストグラムになります.
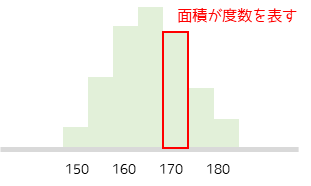
ヒストグラムは1つ1つの棒(ビン)の面積が階級ごとの度数を意味します.棒が長く密集しているほど,データがその階級に集中していることがわかります.ヒストグラムのデメリットは,ビン幅の定義によって見え方が大きく異なることです.ビン幅に定義はないためヒストグラムの見え方は作成者の主観となってしまいます.
ヒストグラムの次によく用いられるのが箱ひげ図になります.箱ひげ図はヒストグラムを90°回転させたようなグラフで,データの分布を四分位数で区切ったグラフになります.箱ひげ図はデータの正確な分布が捉えづらいといったデメリットがあります.特にヒストグラムの山が2つあるような,データが集中している値が2つ以上ある分布を表すことができません.
その他のグラフとしてはバイオリンプロットやストリッププロット,スウォームプロットがあります.これらのグラフはデータ群が複数ある場合に並べて比較しやすいといった共通するメリットがあります.
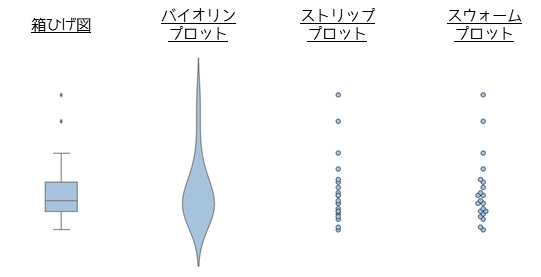
バイオリンプロットはヒストグラムを滑らかにしたようなグラフで,箱ひげ図では捉えづらい分布も表現することができます.近年は箱ひげ図よりもよく用いられる傾向があります.デメリットとしては作成するためにRやPython,有料統計解析ソフトを使用する必要があることと,箱ひげ図に比較して知名度が低いことです.
ストリッププロットは直線状に全てのデータをプロットしたグラフになります.プロットの密集度でデータの分布を判断することができます.箱ひげ図やバイオリンプロットの上に重ねて用いることもあります.ストリッププロットのデメリットはデータ数が多い場合に,密集した値付近の密集度合いがわかりづらい点があります.
スウォームプロットはストリッププロットと同様に全てのデータを直線状にプロットし,重なりがある場合は横に広げてプロットしたグラフになります.データの密集度を横幅で判断することができます.
学術論文では元データの分布をより正確に示すために,スウォームプロットのような全データの情報が分かるグラフを推奨される場合があります.
グラフ作成するならStaatApp
ヒストグラムと箱ひげ図はExcelを用いて,比較的簡単に作成することができます.一方でバイオリンプロットやスウォームプロットはExcelでは作成することができません.
Excelで作成できない分布グラフはRやPython,有料の統計解析ソフトを用いて作成する必要があります.本サイトでは様々なグラフをマウス操作だけで素早く作成する統計解析アプリStaatAppを販売しています.
グラフ作成のためにRやPythonを使いたくないという方や,なるべく安い価格で作りたいという方におすすめです.
》統計解析ソフトStaatAppとは
》StaatAppで行うグラフ作成
グラフの選び方
統計解析においてグラフは様々な種類があります.分析対象のデータ・分析の目的から考える最適なグラフの選び方について,以下のページで解説しています.
参考文献と同じグラフが作成したい!けど,Excelでは難しい…
研究データを取りまとめて,論文執筆を行う際に以下の悩みはないでしょうか.
・参考文献と同じグラフを作成したいけど,Excelなどの表計算ソフトでは対応できない
・有料ソフト(SPSSなど)でも,参考文献と同じグラフを作成できない
・RやPythonで描画したいがプログラムの書き方がわからない
実際に既往研究と同じようなグラフを描画するためには,統計ソフトだけで対応することが難しく,RやPythonを用いたプログラミングが必要な場面が多々あります.
そこで本サイトでは,グラフ作成に関する代行,描画用プログラムの作成サービスを提供しております.本サービスではチャットで連絡を取りながらご希望のグラフを作成したり,お手元のデータで自由にグラフを描画できるプログラムの作成を行っています.
サンプルサイズが小さい場合
サンプルサイズが小さい場合,細かいデータの分布を示す分布グラフはあまり意味をなさなくなります.サンプルサイズが小さい場合や分布を意識する必要がない場合は,箱ひげ図や棒グラフとエラーバーの組み合わせでデータのばらつきを示すことが多いです.
エラーバーは統計解析の1つである仮説検定の結果を示す際にもよく用いられます.
散布図・散布図行列
2つの数量データの分布を表すグラフとしては散布図が用いられます.横軸と縦軸にそれぞれの変数を設定してグラフを作成します.
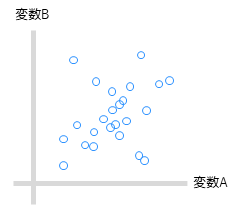
散布図を作成することで,外れ値の検出だけでなく2つの変数の相関関係まで調べることができます.
数量データが複数ある場合は,すべての変数ごとに散布図を作成する散布図行列が利用されます.多変量解析を実施する前にデータの特徴・関連性を調べるためによく用いられます.
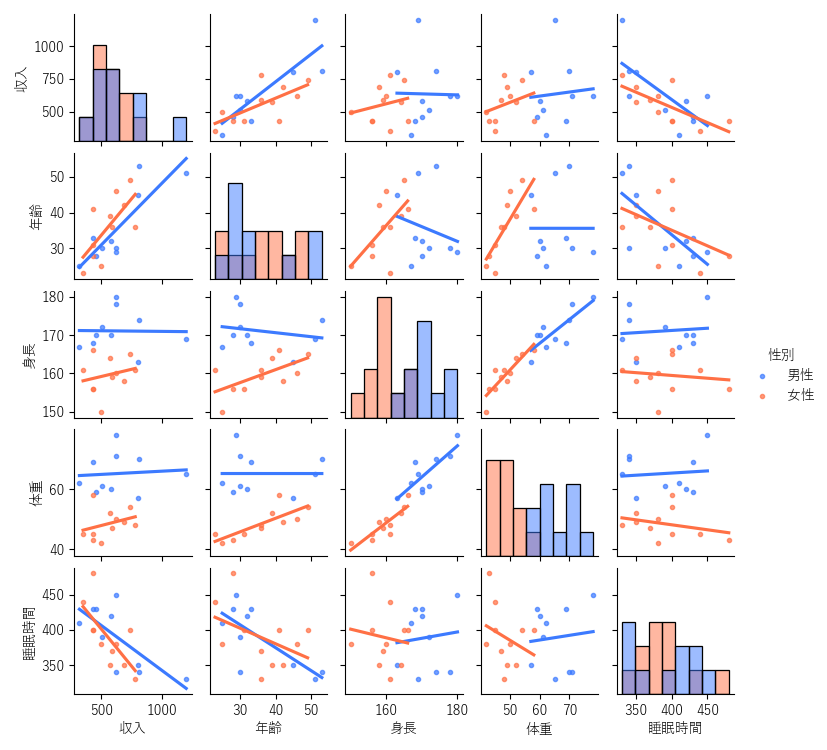
散布図行列の作成はRやPythonの利用が必要ですが,StaatAppの無料機能で作成することができます.
バブルチャート
3つの数量データの分布を表すグラフとしてはバブルチャートがあります.
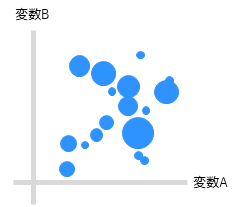
バブルチャートは散布図に加えてプロットの面積で3つ目の変数の値を示します.データ数が多い場合にプロットが重なってしまうといったデメリットがあります.
バブルチャート以外には等高線グラフのような,3次元グラフを使うといった方法があります.因みに4つ以上の量的変数に対しては,視覚的に表現することは難しいです.
StaatAppでは無料機能でバブルチャートを作成することができます.










