データのばらつきを示す統計量である分散と標準偏差について解説します.
ばらつきを調べることの重要性
初めに,統計学においてばらつきを求める重要性について説明します.
下の表のように,10点満点のテストを受けた6人の結果があるとします.

このデータは,平均値といった統計量を用いると2つのテストの結果は”5”になります.しかし,同じ平均値でもデータの実態は全く異なることが表から分かります.
そこで,扱っているデータがどのような性質を持っているのか知るために,平均値だけでなくデータの散らばり具合を表現しようという目的から生まれた統計量が分散と標準偏差になります.
分散の求め方と意味
データのばらつき具合を求める方法として有効なのが,それぞれのデータが平均値からどれだけ離れているのかを調べることです.
先ほどの各データを,平均値からの差で表現し直してみます.

各データは,平均値からどれだけ大きいか・小さいかを表現しています.これを統計学では偏差と言います.
次に,数学のテストとしてどれだけばらつきがあったのかを考えます.その際に,数学の各点数の偏差を足してしまうと0になってしまいます.これは,英語のテストにおいても同様です.
そこで,平均からどれだけ離れているかを調べれば良いので偏差のプラスマイナスが無くなるような方法を考えます.
それが,二乗平均です.以下のように偏差を二乗を合計してからデータの個数で割ることで数学のテストとしてのばらつき具合を調べます.
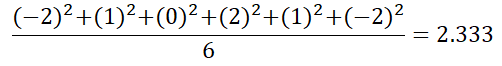
この”2.333”というのが分散です(まだ,二乗平均ではありません).ここまでの計算から分かるように,分散が大きければ大きいほど平均値から離れている値が多いデータであるということが分かります.
標準偏差の求め方と意味
先ほどの偏差と比較して大きな値になっているため,これをデータのばらつき具合とするのは良くありません.そこで,分散を求める過程で二乗計算を行ったので分散をルート計算することで正しいばらつきを表す指標にします.
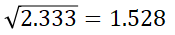
ここで求めた”1.528”がデータのばらつきを表す標準偏差(Standard Deviation)です.
この標準偏差は,「数学のテストの点数は平均点の6点からだいたい1.5点ほど散らばっている」ということを意味しています.
同様に,英語のテストの標準偏差を求めると,”2.944”になります.つまり数学のテストに比べて英語のテストの方が平均点から各点数が散らばっているということを示しています.
これは,点数表を見ても明らかで標準偏差がデータのばらつきを示してることが分かるかと思います.