対応のあるt検定とは
対応のあるt検定とは,同じ個体(人や物)から得られたデータに差があるかを判定する統計学的手法で,個体差が大きい場合に判定の精度が向上します.対応のないt検定とは計算方法が異なるので注意してください.
t検定では2グループの標本平均を比較して,その差が母集団においてもあると言えるのかを確率的に判断します.
例えば,薬の投薬前後や授業の受講前後の差を比較する場合に用いられます.
対応のあるt検定の手順
対応のあるt検定は以下の手順で行います.
① 仮説の設定
帰無仮説は「2群の母平均に差がない」,対立仮説は「2群の母平均に差がある」として設定します.
② 有意水準の決定
有意水準α=0.05または0.01として設定します.一般的にはα=0.05で設定されます.
③ 検定統計量の算出
T値を検定統計量として求めます.
④ p値の算出
検定統計量からp値を算出します.Excelではデータから直接p値を求めることができます.
⑤ 有意差判定
・p値<有意水準であれば,帰無仮説は棄却されて対立仮説を採択 → 「2群の母平均に差がある」
・p値\(\geq\)有意水準であれば,帰無仮説は棄却されない → 「2群の母平均に差があるとは言えない」
仮説検定の考え方や用語については,以下のページで解説しています.
t検定を行なうなら専用ソフトで!
統計アプリStaatAppを用いれば,Excelを用いるより簡単に対応のあるt検定の検定統計量やp値,効果量を算出することができます.
t検定の結果を図示する際に用いられるエラーバーもマウス操作だけで,作成することができます.基本機能は全て無料で,有料版ではマンホイットニーのU検定などのノンパラメトリック検定や多重比較が可能です.
お気軽にダウンロードしてお使いください.
》StaatAppで行う仮説検定
》統計解析アプリStaatApp
例題で用いるデータと仮説の設定
例題では以下のサンプルデータを用います.1人暮らしをしている10人の大学生に,実家で生活していた時と,現在の1日の平均スマホ使用時間を調査した結果です.
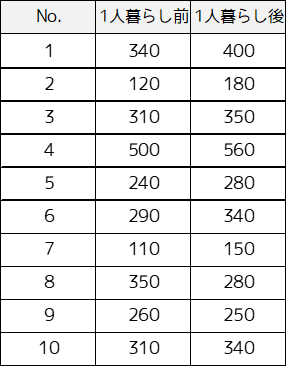
帰無仮説は「1人暮らしの前後でスマホ使用時間(平均使用時間)に差がない」となり,対立仮説は「1人暮らしの前後でスマホ使用時間に差がある」と設定します.
有意水準α=0.05で両側検定を行います.
Excelを用いたp値の計算(データ分析ツールの実行)
実際のExcel画面を用いてp値の計算手順を説明をします.用いているExcelのバージョンはOffice2016になります.
対応のあるt検定で使うツールを選択するために,「データ」タブの「データ分析」をクリックします.

出てきた「データ分析」ウィンドウから,「t検定: 一対の標本による平均の検定」をクリックして「OK」を選択します.
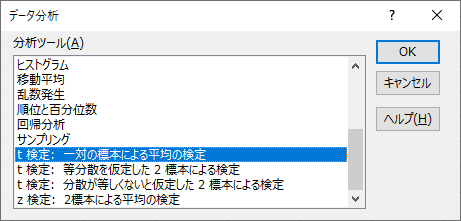
「t検定: 一対の標本による平均の検定」では,入力する項目について説明します.
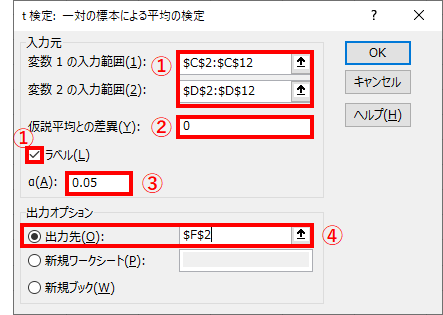
① 準備①で入力したデータのセルを選択します.データの範囲を選択する際に,ラベル(1行目の項目名)まで選択して「ラベル(L)」にチェックを入れます.
② 「仮説平均との差異(Y)」は”0”を入力します.
③ t検定の有意水準を入力します.有意水準α=0.05とする場合は,”0.05”を入力します.
④ 出力先は任意の場所を選択してください.同じシート内の空白のセルを選択すると出力結果が見やすいです.
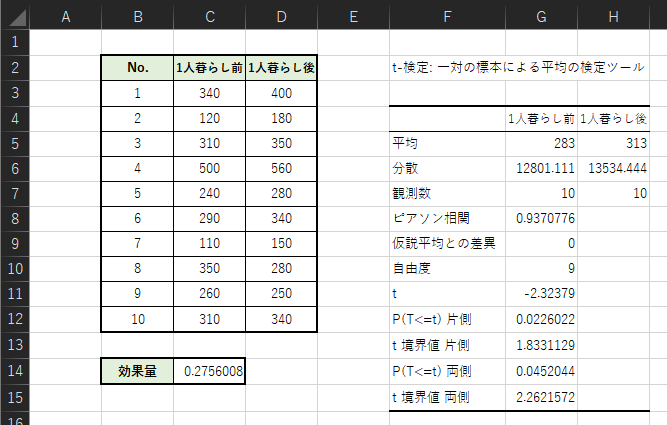
①から④までを入力して「OK」をクリックすると,出力指定したセルに以下の表が作成されます.
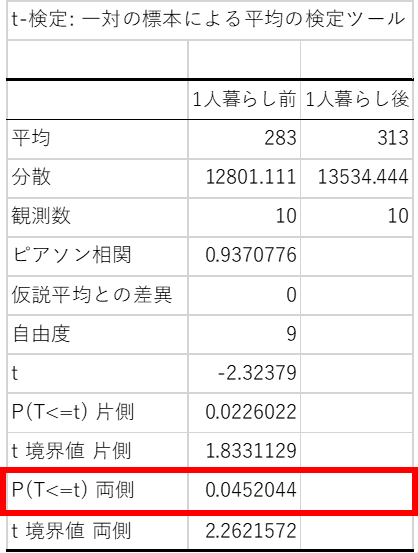
作成された表のうち,両側検定では「P(T<=t) 両側」の行を見ます.これは,両側検定におけるp値を示しており,例題の結果は0.0452..であることが分かります.
p値<有意水準α=0.05であるため2つのグループのデータに有意差があるため,帰無仮説は棄却されます.よって「大学生は1人暮らしの前後でスマホ使用時間に差がある」といった結論が得られます.
※ 表中の”t”は検定統計量,”t境界値 両側”は両側検定における限界値になります.
以上が,Excelを用いた対応のあるt検定の手順になります.
補足① 片側検定の方法
片側検定の方法を解説します.
片側検定は,2つのグループの大小を明らかにしたい場合に行います.例題では帰無仮説は両側検定と同じ,「1人暮らしはスマホの使用時間に影響はない」とした際に,対立仮説は「1人暮らしをするとスマホの使用時間が長くなる」とします.
片側検定において対立仮説を設定する場合は,予め2つのグループの平均値などを比較することで,どちらのグループの値が大きくなりそうか予測しておきます.
分析ツールの実行方法・設定内容は両側検定と同じです.片側検定では出力された「P(T<=t) 片側」の行の結果を用います.
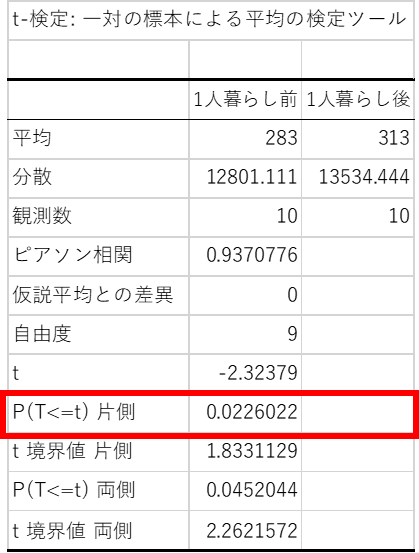
片側検定におけるp値は0.0226..であり,有意水準α=0.05より小さいことが分かります.よって帰無仮説は棄却され,「大学生は1人暮らしをするとスマホの使用時間が長くなる」 といった結論になります.
以上が片側検定の場合の手順になります.
補足② 効果量の求め方(Excel版)
仮説検定の結果として重要な効果量の求め方について,Excelを用いて解説します.
対応のあるt検定の効果量は様々な方法で計算することができますが,ここではCohen’s dという効果量で解説します.
Statistical Power Analysis for the Behavioral Sciences by Jacob Cohen (1988)
Cohen’s dは以下の式で求めることができます.
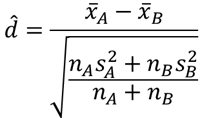
xA,xBは各グループの平均,nA,nBはサンプルサイズ,sA,sBは標本標準偏差になります.Excelではデータ分析ツールの結果を利用して,以下のように求めることができます.
※ C14セルの入力式:=ABS((G5-H5)/SQRT(((G7-1)*G6+(H7-1)*H6)/(G7+H7)-2))
Cohen’s dの値の目安としては次のようになります.
【効果量dの目安】 小:0.2 中:0.5 大:0.8
例題において効果量は小さいため,「1人暮らしの前後でのスマホ使用時間にはそれほど差がない」と言うことができます.
補足③ 用いるデータの前提条件
対応のあるt検定を行う際に,用いるデータの前提条件について説明します.
① 対応のあるデータ
対応のあるt検定は対応のないグループ(異なる個体)のデータに対しては用いることができません.対応のない場合は,対応のないt検定を行います.
② 正規分布に従う
t検定は,パラメトリックな検定になります.用いるデータが正規分布に従うと仮定できる場合に使うことができます.正規分布でない場合は,ノンパラメトリック検定であるウィルコクソンの符号順位検定を行います.
補足④ 手計算の方法
本ページでは検定の手順のみを解説したので手計算で行う方法や,もう少し対応あるt検定について理解したいという方は以下のページも読んでみてください.