フィッシャーの正確確率検定とは
フィッシャーの正確確率検定とは小標本にカテゴリーデータに対して行う仮説検定です．クロス集計表に対して表側と表頭の変数間に関連性があるか，統計学的に判定するために行います．
以下の図はフィッシャーの正確確率検定の考え方です．大学生19人の男女に1人暮らしをしているか調査した例になります．
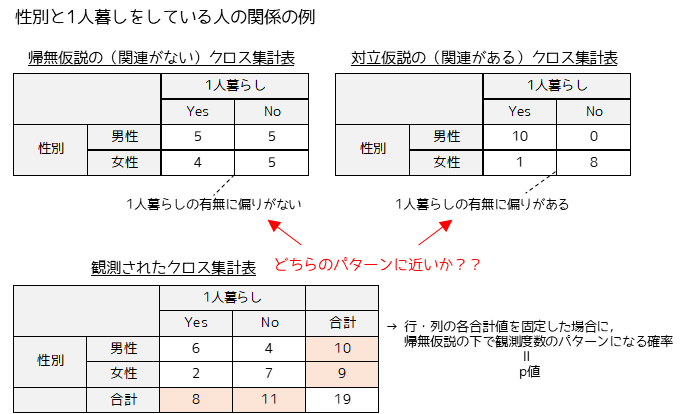
調査した（観測された）結果が関連がない場合，もしくは関連がある場合のパターン（度数配置）のどちらに近いのか考えることで，2つの変数間の関連性を調べます．
観測されたクロス集計表が関係がある場合のクロス集計表に近い場合，2つの変数には関連性があると判定します．例では，「性別と1人暮らしの有無に関係性がある＝男性の方が1人暮らしをする傾向がある」という結論が得られます．
フィッシャーの正確確率検定ではp値を計算するために，クロス集計表の全てのパターン（度数配置）を計算する必要があるため膨大な計算が必要になります．
サンプルサイズが大きい場合は計算量が多くなるため，類似した手法であるカイ二乗検定（独立性の検定）を行います．カイ二乗検定との詳しい使い分け方は補足④で紹介しています．
フィッシャーの正確確率検定の手順
フィッシャーの正確確率検定は以下の手順で行います．
① クロス集計表の作成
単純データからクロス集計表を作成します．
② 仮説の設定
帰無仮説は「クロス集計表の表側と表頭は関連性がない」，対立仮説は「クロス集計表の表側と表頭は関連性がある」として設定します．
③ 有意水準の決定
有意水準α＝0.05または0.01として設定します．一般的にはα＝0.05で設定されます．
④ p値の算出
クロス集計表からp値を算出します．検定統計量計算せずに直接p値を求めることがこの検定方法の特徴です．
⑥ 有意差判定
・p値＜有意水準であれば，帰無仮説は棄却されて対立仮説を採択 → 「クロス集計表の表側と表頭は関連性がある」
・p値\(\geq\)有意水準であれば，帰無仮説は棄却されない → 「クロス集計表の表側と表頭は関連性があるとは言えない」
仮説検定の考え方や用語については，以下のページで解説しています．
検定結果を間違えたくない方へ
Excelを用いた計算方法より簡単・正確に，フィッシャーの正確確立検定の検定結果を調べることができる統計解析アプリStaatAppを販売しております．
StaatAppではフィッシャーの正確確立検定以外にも様々なクロス集計表の分析・仮説検定をクリックだけで実行することができます．詳細は以下のページをお読みください．
》StaatAppで行うクロス集計表の分析
》統計解析アプリStaatApp
例題で用いるデータと仮説の設定
例題では以下のサンプルデータを用います．大学生19人に対して1人暮らし有無を調査した例です．
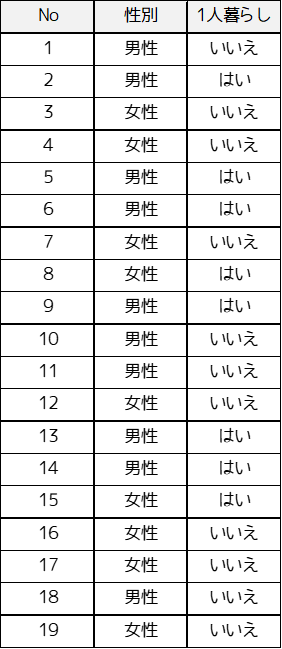
フィッシャーの正確確率検定を行い性別によって副業有無に差があるかを判定します．
帰無仮説は「性別と1人暮らしの有無には関連性がない」となり，対立仮説は「性別と1人暮らしの有無には関連性がある」と設定します．
有意水準α＝0.05で行います．
Excelを用いたp値の計算手順
Excelを用いたp値の計算手順について説明します．
以下のようなクロス集計表の作成と度数配置の確率を計算して，p値を求めます．
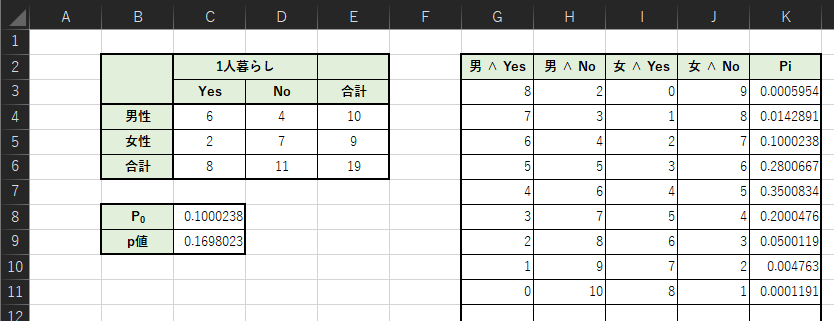
各セルの入力式は以下になります．
・C8：=COMBIN(E4,C4)*COMBIN(E5,C5)/COMBIN(E6,C6)
・C9：=SUMIF(K3:K11,”<=”&C8)
・G3：=$C6-I3
・H3：=$E4-G3
・I3：0
・J3：=$E$5-I3
・K3：=COMBIN(E$4,G3)*COMBIN(E$5,I3)/COMBIN(E$6,C$6)
p値の計算方法について解説します．
① 基準値P0を求める【C8】
p値を求める上で基準となるP０を計算します．例題ではP０の計算式は以下のようになります．
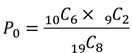
Excelでは組み合わせの計算をCOMBIN関数を用いて行います．
② 0になり得るセルを求める【C5】
クロス集計表の観測度数が入力されている4つのセルのうち0になる可能性があるセルを求めます．この後の計算で各列・行の合計値が同じ場合の観測度数の全てのパターンを求める際に，基準となるセルを見つけるために行います．
0になり得るセルの求め方は，クロス集計表の各列・行の合計値を見た際に両方小さい値に該当するセルになります．
例題では1人暮らしでは’Yes’の列の合計値が小さく，性別では’女性’の行の合計値が小さいため”C5”セルつまり’女性かつ1人暮らし’に該当するセルが求めたいセルになります．
③ 0になり得るセルの取る値を全て求める【I列】
②で求めたセルの各列・行の合計値が同じ場合に取り得る値を全て求めます．このとき，0が最小値で最大値は該当するセルの列・行の合計値うちが小さい値になります．
例題では”C8”セルが0になり得るセルですので最小値が0で最大値が8になります．
入力する際に，Excel的な方法としては０を入力したセルの右下部分にカーソルを当てて十字に変化したら任意のセルまでドラッグをします．ドラッグした最終セルの右下のメニューボタンをクリックして「連続データ(S)」を選択すると０からの連続した値を入力することができます．
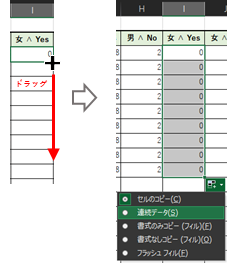
④ 残りのセルのなり得る値を求める【G列】【H列】【J列】
③で求めた値を基準に残りのセルのとり得る値を求めます．③で求めた値を列・行の合計値から引くことで計算することができます．
例題では最初に’男性かつ1人暮らし’に該当する，”C4”セルのなり得る値を求めます．
Excelでは絶対参照を用いて式を入力してから，オートフィル機能を使うことで簡単に計算することができます．
’$’は絶対参照を示す記号で，オートフィル機能を使った際も’$’の後ろの記号は固定となり常に指定された値に該当するセルを参照します．上記の式の”I3”は絶対参照では無く，相対参照のためオートフィル機能を使うと自動的に参照先が変化します．
残りのセル，’男性かつ１人暮らしではない’に該当する”D4”セルと’女性かつ１人暮らしでは無い’に該当する”D5”セルのなり得る値も同様に求めます．
※ ②で求めたセルによって③④で入力する式は異なることに注意してください．紹介した式をコピペしたい場合は，”C5”セルに②で求めたい値になるように扱うクロス集計表を書き換えてみてください．
⑤ 各パターンになる確率Piを求める【K列】
③と④で求めた各セルがなり得る値の全パターンに対して，各パターンが起こりうる確率Piを求めます．
例えば，一番上の行の”C5”セルが0のパターンになる確率Piは以下の式で求めることができます．
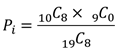
Excelでは組み合わせの計算をCOMBIN関数を用いて行います．残りの確率Piは，オートフィル機能を使って計算します．
⑥ p値を求める【C9】
フィッシャーの正確確率検定のp値は，基準値P0以下の確率Piの和で計算することができます．
ExcelではSUMIF関数を用いることで特定の条件を満たす，セルの和を計算することができます．
以上が，p値の計算方法になります．
例題では有意水準をα＝0.05としてp値は0.169..だったので，有意水準よりp値は大きいことが分かります．これより，「大学生が1人暮らしをするかどうかは性別が影響するとは言うことができない」といった消極的な結論が得られます．
補足① Pythonを使ったp値の求め方
Pythonを使った正確確率検定の求め方について紹介します．Pythonではpandasとscipyライブラリを用いることで簡単にp値を求めることが可能です．
以下が，Pythonにおける正確確率検定の記述例です．
import pandas as pd
import scipy.stats as st
df = pd.DataFrame([[6, 4], # 男性行[Yes, No]
[2, 7]]) # 女性行[Yes, No]
_, p = st.fisher_exact(df)
print(f'p値 = {p :.7f}')
# 出力結果
p値 = 0.1698023Pythonで求めたp値は，Excelで求めた値と全く同じことがわかります．
補足② 効果量（クラメールの連関係数）
仮説検定の結果として重要な統計量として効果量があります．効果量は要因が持つ本来の性質であり，サンプルサイズやデータの単位に依存しない指標となります．
フィッシャーの正確確率検定の効果量はクラメールの連関係数と呼ばれます．
クラメールの連関係数については以下のページで計算方法まで解説しています．
補足③ 正確確率検定の前提条件
正確確率検定を行う際に用いるデータの前提条件について説明します．
① 2×2クロス集計表
2×2クロス集計表の分析のみに用いることができます．2×3クロス集計表などの分析には用いることができません．
② 質的データ
正確確率検定で用いるデータは質的データである必要があります．正確確率検定を行う前に作成するクロス集計表自体も質的データであることが作成する前提条件となります．
③ 累積度数
アンケートを行い，割合を用いて集計した結果には用いることができません．クロス集計表でも同様に，ある項目に対して何人いたかといった度数で表現したデータが前提条件です．
補足④ カイ二乗検定との関係
正確確率検定のようにクロス集計表に対する独立性の検定としてカイ二乗検定があります．カイ二乗検定はカイ二乗分布を用いて近似することによりp値を求めます．
正確確率検定は’正確’と呼ばれる通り，近似をせずに組み合わせの確率を計算してp値を求めます．観測度数が小さい場合に用いることができますが，観測度数が多いほど計算量が多くなるというデメリットがあります．
一般的には，クロス集計表のセルの値の最小値が5未満の場合はカイ二乗検定を行うことができず正確確率検定を行います．
セルの最小値が5以上の場合は，カイ二乗検定を行うことが多いですが正確確率検定を行っても問題ありません．(寧ろ計算が可能であれば正解確率検定を行なうべきです．)
