スティール・ドゥワス(Steel=Dwass)検定とは
スティール・ドゥワス検定はマンホイットニーのU検定を,3群以上の標本に対して使えるようにした方法です.
多重比較の中で最も一般的な手法である,テューキー法のノンパラメトリック版でもあり,比較方法としては全ての2群同士を代表値の差が大きいか否かで判断します.
以下の図がスティール・ドゥワス検定の考え方になります.給与に対する満足度を役職ごとに比較する例になります.
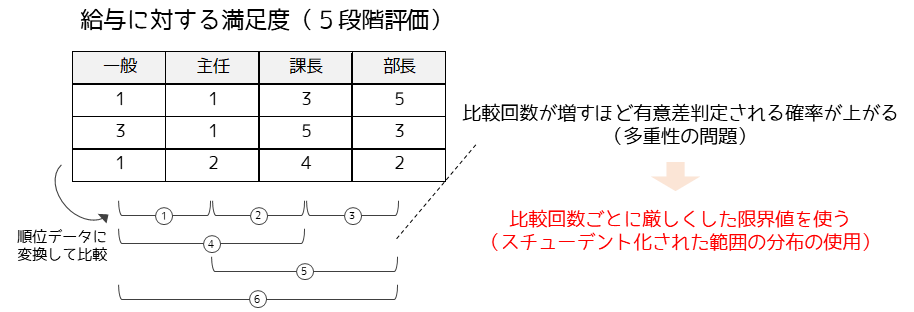
4群に対して2群の代表値の差の比較を行なう場合,検定回数は6回必要になります.有意水準α=0.05で検定を6回繰り返すと有意になる確率は26%(=1-(1-0.05)6)に上昇します(多重性の問題).
多重性の問題を解決するためにスティール・ドゥワス検定では,比較する群数が増えるごとに厳しくした限界値(分布)を用いて仮説検定を行います.
スティール・ドゥワス検定は比較するグループのサンプルサイズ(データ数)が一致していない場合でも検定を行うことが可能です.
スティール・ドゥワス検定の手順
スティール・ドゥワス検定は以下の手順で行います.
① 仮説の設定
帰無仮説は「各群間の母集団に差がない」,対立仮説は「各群間の母集団に差がある」として設定します.
② 有意水準の決定
有意水準α=0.05または0.01とします.一般的には0.05で設定されます.スティール・ドゥワス検定は両側検定のみとなります.
③ 検定統計量の算出
具体的な計算手順は,Excelを用いた方法で解説しています.
④ 有意差判定
限界値<検定統計量であれば,帰無仮説は棄却されて対立仮説を採択 → 「比較した2群の母集団に差がある」
限界値\(\geq\)検定統計量であれば,帰無仮説は棄却されない → 「比較した2群の母集団に差があるとは言えない」
仮説検定の考え方や用語については,以下のページで解説しています.
検定結果を間違えたくない方へ
Excelを用いた計算方法より簡単・正確に,スティール・ドゥワス検定の検定結果を調べることができる統計解析アプリStaatAppを販売しております.
StaatAppではスティール・ドゥワス検定以外にも様々なノンパラメトリック検定・多重比較をマウス操作だけで実行することができます.詳細は以下のページをお読みください.
》StaatAppで行う仮説検定
》統計解析アプリStaatApp
例題で用いるデータと仮説の設定
例題では以下のサンプルデータを用います.ある会社の社会人に対して給与に対する満足度を,5段階で調査した例になります.
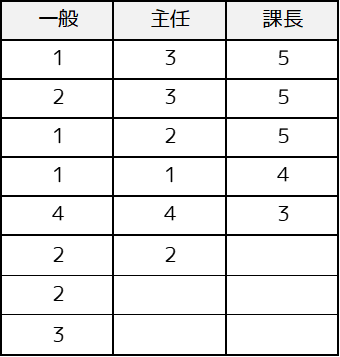
帰無仮説は「比較した役職ごとに給与に対する満足度に差はない」となり,対立仮説は「比較した役職ごとに給与に対する満足度に差がある」と設定します.
有意水準α=0.05で検定は行います.
Excelを用いた計算手順
Excelを用いた検定統計量の計算手順について説明します.
以下のような表を作成して,検定統計量Tを求めます.(一般→A,主任→B,課長→Cとして入力しています)
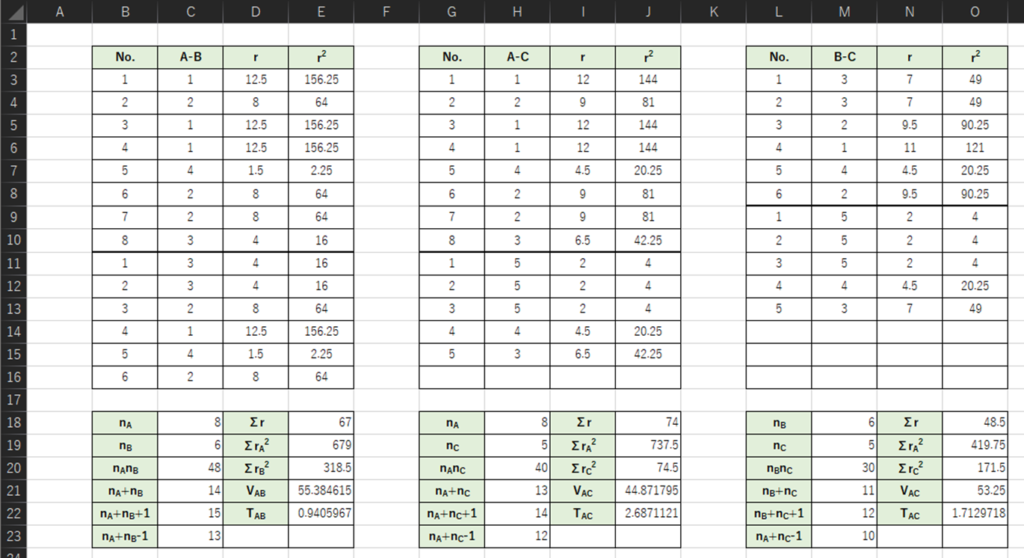
各セルの入力式は以下のようになります.
・D3:=RANK.AVG(C3,C$3:C$16)
・E3:=D3^2
・E18:=SUM(D3:D10)
・E19:=SUM(E3:E10)
・E20:=SUM(E11:E16)
・E21:=(C20/(C21*C23))*(E19+E20-(C21*C22^2)/4)
・E22:=(E18-(C18*C22)/2)/SQRT(E21)
計算手順と用いた関数について説明します.群Aと群B(一般と主任)を比較する手順で説明します.
① 比較するデータを1列で入力する【C3-16】
比較するデータを1列で入力します.入力する際は,上下で群が分かれるように入力してください.
例では太線を境界として群が分かれています.
② 順位と順位の2乗を求める【D3-16】【E3-16】
入力したデータの順位を求めます.順位はRANK.AVG関数を用いて求めることができます.
RANK.AVG関数の引数:RANK.AVG(“順位を求めたい値”,”順位を比較する範囲”)
順位データを求めたら,隣の列にその値を2乗した値を算出します.
③ サンプルサイズと計算用の各項を求める【C18-23】
比較する各群のサンプルサイズと,サンプルサイズから計算用の項を求めます.
nAは群A,nBは群Bのサンプルサイズになります.
④ 順位和を求める【E18】
群Aの順位和を求めます.群Bの順位和でも計算は可能ですが,ここでは計算方法を統一するために上側の群の順位和をΣrとして求めます.
特定の範囲の合計値はSUM関数を用いて計算します.
⑤ 各群の順位の2乗値の和を求める【E19-20】
各群の順位の2乗値の和を求めます.④と同様にSUM関数で求めることができます.
合計するデータの範囲に注意してください.
⑥ 補正係数Vを求める【E21】
マンホイットニーのU検定で算出する検定統計量を補正するための,補正係数Vを求めます.補正係数は以下の式で求めることができます.
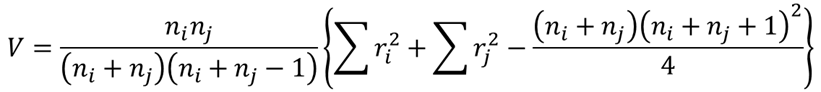
iはA,jはBとなり事前に計算した各セルを用いて計算することができます.
⑦ 検定統計量Tを求める【E22】
検定統計量Tを求めます.検定統計量はマンホイットニーのU検定統計量を補正係数で割った値となります.検定統計量は以下の式で求めることができます.
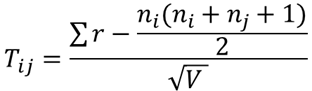
⑧ 残りの群間で①から⑦を繰り返す
⑦までの手順で群Aと群Bの検定統計量を求めることができたので,同様の手順(コピペ)で残りの群間の検定統計量を求めます.
コピペした際は,サンプルサイズと順位和のデータ範囲を修正する必要がある点に注意してください.
有意差判定の方法
Excelでの計算手順で求めた検定統計量とスチューデント化された範囲の分布を用いて有意差を判定します.
スチューデント化された範囲の分布の見方は,行が自由度で列が群数になります.スティール・ドゥワス検定では自由度vが∞となる行の値を用います.
例題では群数が3なので,スチューデント化された範囲の分布から3.31という値を読み取り,\(\sqrt 2\)で割った値2.34..が限界値になります.
群Aと群B(一般と主任)を比較した検定統計量は0.940..であったので, 限界値\(\geq\)検定統計量となり有意差がないと判定できます.群Bと群C(主任と課長)も同様です.
群Aと群C(一般と課長)を比較した検定統計量は2.68..であるので,限界値<検定統計量となり有意差があると判定できます.結論としては「一般社員と課長の給与に対する満足度に差がある」となります.
補足① スチューデント化された範囲の分布
スティール・ドゥワス検定の検定表として用いる,スチューデント化された範囲については以下の通りになります.
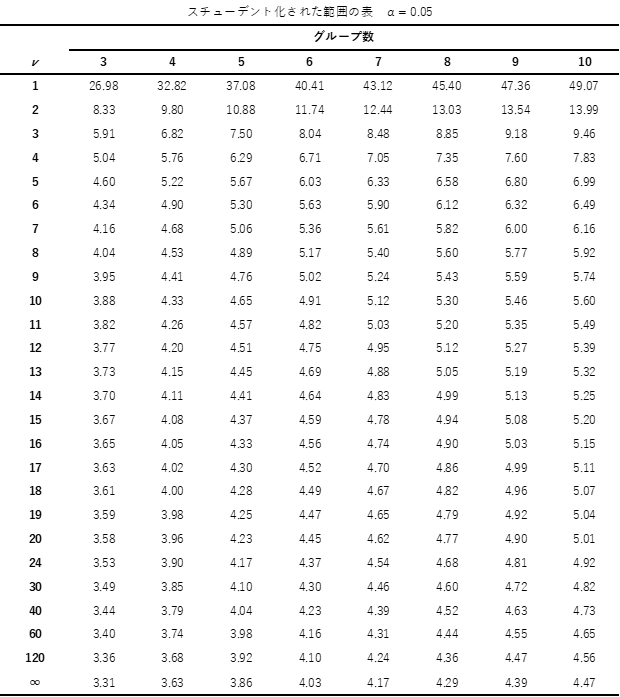
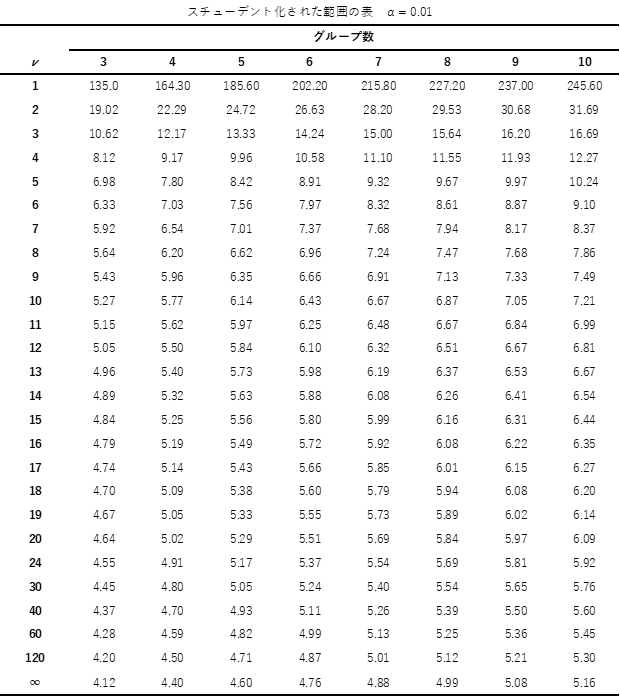
補足② 効果量について
仮説検定の結果として重要な効果量の求め方について紹介します.
多重比較では比較した2群ごとに効果量を計算する必要があります.効果量は様々な方法で計算することができますが,ノンパラメトリック検定の効果量rは,以下の式で求めることができます.
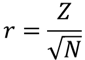
効果量と検定力分析入門 水本・竹内(2010)
※ 効果量には様々な計算方法があるため,論文などでは引用元もしくは計算式を示す必要があります.
Zは検定統計量を標準化(Z変換)した値,Nはサンプルサイズになります.
Excelを用いたノンパラメトリック検定の効果量の求めた方は,以下のページの解説しています.
補足③ 検定の前提条件
3群以上のデータの差の比較を行う多重比較には様々な手法があります.多重比較の1つであるスティール・ドゥワス検定を行う際に,用いるデータの満たすべき条件について説明します.
① 対応のないデータ
比較する2つのグループは対応のない場合である(異なる個体のデータ)である必要があります.対応のある場合は,どのようなデータに対しても検定可能なボンフェローニ補正を行います.
② ノンパラメトリックなデータ
スティール・ドゥワス検定はノンパラメトリックなデータに対して行います.用いるデータの母集団が正規分布と仮定できる場合は,テューキー法などがあります.