ブルンナー・ムンチェル検定とは
ブルンナー・ムンチェル検定とは,対応のない2群の差の検定(対応のないt検定)のノンパラメトリック版です.順序尺度以上のデータに対して用いることができます.
ノンパラメトリックの対応のない2群の差の検定としては,マンホイットニーのU検定が一般的に使われますが,ブルンナー・ムンチェル検定は2群の等分散性がない場合にも使うことができます.
ブルンナー・ムンチェル検定の検定統計量はサンプルサイズが小さい場合はt分布に従い,大きい場合は標準正規分布に従います.
サンプルサイズが非常に小さい場合(n<8)は並べ替え検定を行う必要があります.
ブルンナー・ムンチェル検定の手順
ブルンナー・ムンチェル検定は以下の手順で行います.
① 仮説の設定
帰無仮説は「2群の母集団に差がない」,対立仮説は「2群の母集団に差がある」として設定します.
② 有意水準の決定
有意水準α=0.05,もしくは0.01で設定します.一般的には有意水準α=0.05と設定されます.
③ 検定統計量の算出
具体的な計算手順は,Excelを用いた方法で解説しています.
④ p値の算出
検定統計量からp値を算出します.サンプルサイズによって用いる分布が異なります.
④ 有意差判定
・p値<有意水準であれば,帰無仮説は棄却されて対立仮説を採択 → 「2群の母集団に差がある」
・p値\(\geq\)有意水準であれば,帰無仮説は棄却されない → 「2群の母集団に差があるとは言えない」
統計的仮説検定の考え方や用語については,以下のページで解説しています.
検定結果を間違えたくない方へ
Excelを用いた計算方法より簡単・正確に,ブルンナー・ムンチェル検定の検定結果を調べることができる統計解析アプリStaatAppを販売しております.
StaatAppではブルンナー・ムンチェル検定以外にも様々なノンパラメトリック検定をマウス操作だけで実行することができます.詳細は以下のページをお読みください.
》StaatAppで行う仮説検定
》統計解析アプリStaatApp
例題で用いるデータと仮説の設定
例題では以下のサンプルデータを用います.2つの会社の従業員から調査した,働き方に対する満足度(5段階評価)になります.
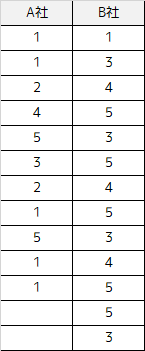
帰無仮説は「働き方の満足度に差がない」となり,対立仮説は「働き方の満足度に差がある」と設定します.
有意水準α=0.05で検定は行います.
Excelを用いた計算方法
Excelを用いたp値の計算手順について説明します.
以下のような表を作成して,検定統計量Wとp値を求めます.(16行目以降もサンプルデータは入力されています)
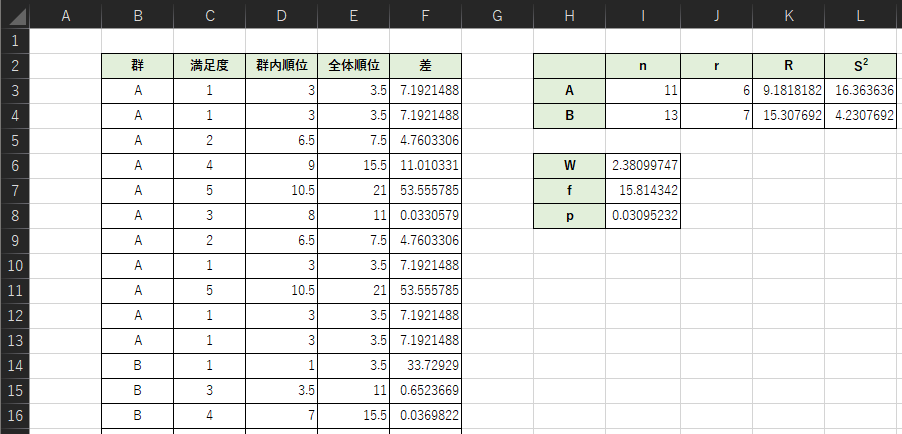
各セルの入力式は以下のようになります.
・D3:=RANK.AVG(C3,C$3:C$13,1)
・D14:=RANK.AVG(C14,C$14:C$26,1)
・E3:=RANK.AVG(C3,C:C,1)
・F3:=(E3-D3-K$3+J$3)^2
・F14:=(E14-D14-K$4+J$4)^2
・I3:=COUNTIF(B3:B26,”=A”)
・J3:=(I3+1)/2
・K3:=SUM(E3:E13)/I3
・L3:=(1/(I3-1))*SUM(F3:F13)
・I6:=ABS((I3*I4*(K4-K3))/((I3+I4)*SQRT(I3*L3+I4*L4)))
・I7:=((I3*L3+I4*L4)^2)/((((I3*L3)^2)/(I3-1))+((I4*L4)^2)/(I4-1))
・I8:=TDIST(I6,I7,2)
入力式と計算手順について解説します.
① データの入力【B列】【C列】
群(会社)と値(満足度)を各1列にデータを入力します.群は上下で分かれるように入力します.
② 群内順位を求める【D列】
値を群ごとの順位データに変換します.
順位データはRANK.AVG関数を用いて計算します.RANK.AVG関数の引数は以下になります.
RANK.AVG(“順位に変換する値”,”順位の対象となるデータ群(各群のデータ範囲)”,1)
※ 例題では値が小さいほど順位が高くなるように計算します.
群ごとに対象のデータ範囲が異なるので注意してください.
③ 全体順位を求める【E列】
2群を合わせた順位に変換します.②と同様にRANK.AVG関数を用いて計算します.
”順位の対象となるデータ群”は,データの範囲はAとBを合わせた範囲になります.
④ サンプルサイズを求める【I3】【I4】
各群のサンプルサイズを求めます.COUNTIFS関数を用いて,「B列」に”A”と”B”がいくつあるかカウントします.
⑤ 各群の平均群内順位を求める【J3】【J4】
各群の群内順位の平均を計算します.郡内順位を用いずに,以下の式で簡単に求めることができます.
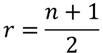
⑥ 各群の平均全体順位を求める【K3】【K4】
各群の全体順位の平均を計算します.群ごとに全体順位の和を,サンプルサイズで割ることで求めることができます.
⑦ 各群の順位データの不偏分散を求める【F列】【L3】【L4】
群ごとに順位データから不偏分散を計算します.不偏分散S2は以下の式で求めることができます.
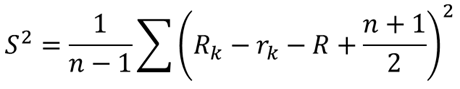
Rkは各全体順位,rkは各群内順位,Rは⑥で求めた平均全体順位になります.
ExcelではΣ内の値(データごとの平均からの差)をF列で計算してから,SUM関数を用いて不偏分散を計算します.
⑧ 検定統計量Wを求める【I6】
検定統計量を計算します.検定統計量Wは以下の式での求めることができます.
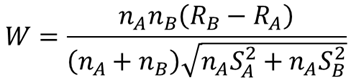
⑨ 自由度fを求める【I7】
t分布の自由度を計算します.自由度fは以下の式で求めることができます.
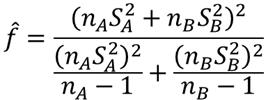
⑩ p値を求める【I8】
検定統計量と自由度からp値を計算します.サンプルサイズが小さい場合,検定統計量Wは自由度fのt分布に従います.
Excelではt分布のp値をTDIST関数で求めることができます.
TDIST関数の書き方:=TDIST(“検定統計量”,”自由度”,2(両側確率))
例題では計算結果からp値は0.0309…となりました.よって帰無仮説は棄却され「2つの会社で働き方の満足度に差がある」といった結論が得られます.
※ 自由度が少数の場合は以下の数式を用いることで,p値を算出することができます.
=MIN(1-BETA.DIST(I7/(I7+I6^2),I7/2,1/2,TRUE),BETA.DIST(I7/(I7+I6^2),I7/2,1/2,TRUE))
補足① サンプルサイズが大きい場合
Excelを用いた計算例では,サンプルサイズが小さい場合のブルンナー・ムンチェル検定を紹介しました.サンプルサイズが大きい場合は,検定統計量Wは標準正規分布に近似することができます.
サンプルサイズが大きい場合の目安としては,両群を合わせたデータ数が50以上の場合です.
標準正規分布のp値はExcelでは,NORMSDIST関数を用いて計算することができます.
標準正規分布のp値(両側)の計算式:=2*(1-NORMSDIST(“検定統計量”))
補足② データの前提条件
補足①に加えて,用いるデータの前提条件を解説します.
① ノンパラメトリックなデータ
ブルンナー・ムンチェル検定はノンパラメトリックな(=正規分布でない)データに対して行います.用いるデータが正規分布と仮定できる場合は,ブルンナー・ムンチェル検定を行うことも可能ですが,多くの場合で対応のないt検定を行います.
② 順序尺度
名義尺度のデータに対しては用いることができません.名義尺度はデータの大小に意味が無い,つまり順位和を求めることができないことから明らかです.名義尺度のデータの差や関連性を分析する際は,クロス集計表を用います.
③ 対応のないデータ
比較する2つのグループは対応のない場合である(異なる個体のデータ)である必要があります.対応のある場合は,ウィルコクソンの符号順位和検定を行いましょう.
》対応のある・対応のないとは
》ウィルコクソンの符号順位和検定
④ 不等分散の場合
冒頭で説明したようにブルンナー・ムンチェル検定は,マンホイットニーのU検定において2群の等分散性が仮定できない場合に行う検定方法です.等分散性が仮定できる場合は,マンホイットニーのU検定を行うのが一般的です.










