多変量解析とは

多変量データとは,複数のデータ(変数)が組み合わさったデータになります.
多変量データの分析を行う手法を多変量解析と言います.多変量解析ではデータ間での関連性やデータが持つ意味の抽出,予測式の作成を行います.
ある個体に対して様々な情報を集めた際に行う手法が多変量解析です.
例えば複数の社会人から年収・年齢・性別・結婚有無といったデータを集めた際に,多変量解析を行うことで年収に影響を及ぼしている要因は何かを調べることができます.
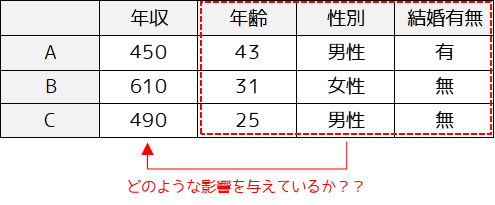
また,年収が未知の社会人のデータがある場合,年齢・性別・結婚有無といった他のデータから予測することができます.
多変量解析の分類
多変量解析は様々な統計学的手法の総称になります.扱うデータの種類や目的によって適した手法を選ぶ必要があります.
手法を選ぶ際にまず考えるのが,分析の目的になります.多変量解析は大きく2つの目的に分類することができます.
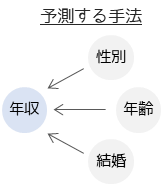
1つ目が「予測」と呼ばれる手法になります.代表例として,重回帰分析やロジスティック回帰分析があります.「予測」を目的とする多変量解析では,多変量データを結果(目的変数)と原因(説明変数)に分けて考えます.結果に対する原因は何かを分析したい場合に行うのが「予測」の手法です
「予測」の手法では,分析結果から結果を導くための予測式を求めることもできます.
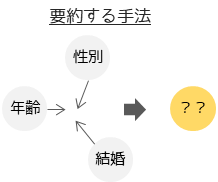
2つ目が「要約」と呼ばれる手法です.代表例としては,主成分分析やクラスター分析などがあります.「要約」を目的とする多変量解析では,多変量データを結果と原因に分けることはしません.多変量データを横並びで考えてデータの持つ特性を分析したり,原因(説明変数)に影響を与えている潜在的な要因(潜在変数)を分析したい場合に行います.
分析の目的を定めたら,扱うデータの種類によって用いる手法を選択します.考えるべきポイントは,扱うデータの種類がカテゴリーデータもしくは数量データであるかです.
例えば,目的変数が2つの分類(Yes/Noなど)を持つカテゴリーデータで,説明変数が数量データである場合はロジスティック回帰分析を行います.
以下の表が主な多変量解析における扱うことができるデータの種類と数になります.
|
手法
|
目的 | 目的変数 | 説明変数 | ||
| カテゴリーデータ | 数量データ | カテゴリーデータ | 数量データ | ||
| 重回帰分析 | 予測 | 1 | 複数 | ||
| 数量化Ⅰ類 | 予測 | 1 | 複数 | ||
| 判別分析 | 予測 | 1(2値) | 複数(2値) | 複数 | |
| ロジスティック回帰分析 | 予測 | 1(2値) | 複数 | ||
| 多項ロジスティック回帰分析 | 予測 | 1(多分類) | 複数 | ||
| 数量化Ⅱ類 | 予測 | 1(多分類) | 複数 | ||
| 一般化線形混合モデル | 予測 | 1(2値) | 1 | 複数 | |
| Cox比例ハザード回帰 | 予測 | 2(生存時間) | 複数 | ||
| 主成分分析 | 要約 | 複数 | |||
| 因子分析 | 要約 | 複数 | |||
| 共分散構造分析 | 予測・要約 | 複数 | 複数 | ||
| クラスター分析 | 要約 | 複数 | |||
| コレスポンデンス分析 | 要約 | 2 | |||
| 数量化Ⅲ類 | 要約 | 複数 | |||
| 決定木 | 予測 | 1 | 複数 | ||
統計学におけるデータの種類については,以下のページで具体的に解説しています.
多変量解析の実行方法
多変量解析は非常に複雑な計算が必要なため,重回帰分析を除いて手計算やExcelを用いて行うことは難しいです.多変量解析は一般的にRやPython,有料統計解析ソフトを用いて行われます.
本サイトでは2つの方法を紹介しています.
① Pythonを用いた方法
Pythonを用いた方法に初めてプログラミングを行う方でもわかるように解説しています.
② 統計解析アプリ(StaatApp)を用いた方法
StaatAppとは任意のデータを数クリックだけで統計解析ができるPC用アプリです.プログラミングに苦手意識ある方や,できるだけ学習コストを小さくして正確な解析結果を得たい方にはおすすめです.
初めての方はほぼ全ての機能を無料で利用できるので,お気軽にダウンロードしてお使いください!
主な多変量解析
主な多変量解析の手法について解説します.
重回帰分析

重回帰分析とは,多変量解析で最もよく用いられる分析手法になります.回帰分析の原因(説明変数)が複数あるバージョンです.
結果に対して影響を及ぼしている原因は何かを調べる際に用います.また,「予測」の手法なので分析結果から予測式を求めることもできます.
扱えるデータは,数量データのみとなります.多変量データにカテゴリーデータが含まれている場合は,他の分析手法を用いるかもしくは,ダミー変数を使う必要があります.
数量化Ⅰ類
数量化Ⅰ類は,重回帰分析と類似した手法で違いは説明変数がカテゴリーデータであることです.
数量化Ⅰ類では,結果に対する原因の影響度や結果の予測式を求めることができます.
判別分析
判別分析は,数量化Ⅰ類とは反対に目的変数がカテゴリーデータで説明変数が数量データである場合に行います.厳密には,説明変数がカテゴリーデータでも2つの分類であれば行うことができます.
ロジスティック回帰分析と類似する手法ですが,判別分析では目的変数の分類がすでに分かっておりその分類を判別するために行います(後ろ向き研究).医療分野では,疾患が発症した後に,ある被験者が疾患であるかを判断するために用います.
扱うデータは,正規分布に従う必要があります.
ロジスティック回帰分析
ロジスティック回帰分析は,判別分析と同様に目的変数がカテゴリーデータで説明変数が数量データである場合に行います.
ロジスティック回帰分析では,原因が複数ある場合に結果を予測するために行います(前向き研究).医療分野では,疾患が発生する前に,ある被験者が疾患を発症するか予測するために用います.また,「1日の喫煙本数の差によって死亡リスクが何倍になるか」を予測することもできます.
扱うデータは正規分布に従う必要がないので,判別分析より優先的に使われます.
》ロジスティック回帰分析の手順(Python)
》StaatAppで行うロジスティック回帰分析
多項ロジスティック回帰分析
多項ロジスティック回帰分析は,目的変数が3カテゴリー以上の多分類の場合に行うロジスティック回帰分析です.
多項ロジスティック回帰分析では目的変数の”カテゴリー数-1”個の回帰式が作成されます.
数量化Ⅱ類
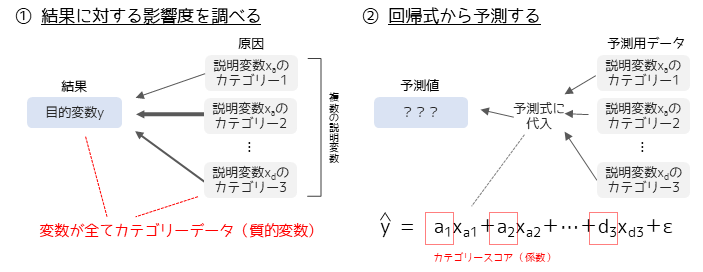
数量化Ⅱ類は,重回帰分析と類似した手法で違いは目的変数と説明変数が数量データであることです.数量化Ⅱ類では,結果に対する原因の影響度や結果の予測式を求めることができます.
一般化線形混合モデル
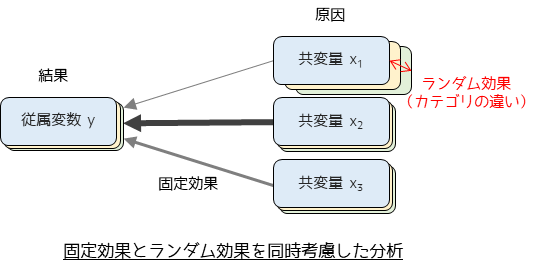
一般化線形混合モデル(Generalized Linear Mixed Models; GLMM)は,統計モデルの一つで,固定効果とランダム効果の両方を考慮します.固定効果はすべての個体やグループに共通する効果を示し,ランダム効果は個体やグループ間のランダムな変動を捉えます.様々なデータに合わせて柔軟なモデルを作成できるため使用場面は多岐にわたりますが,特に繰り返し測定データや階層的なデータ構造を持つデータの分析に適しています.
近年の学術分野では非常によく用いられるかつおすすめの分析手法になります.
Cox比例ハザード回帰
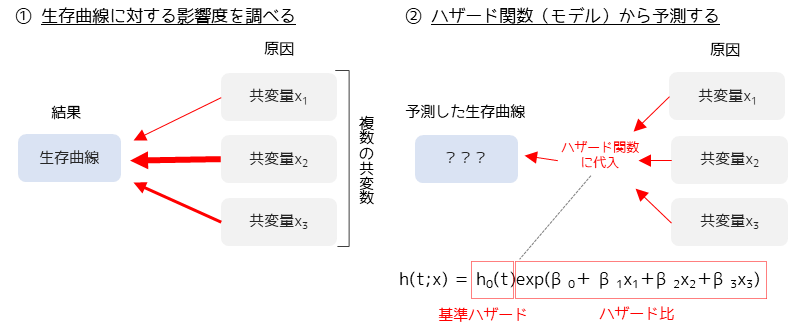
Cox比例ハザード回帰とは,生存時間データのための重回帰分析です.生存時間データは生存曲線で表され,イベント発生までの時間を示すデータになります.Cox比例ハザード回帰を行うことで,生存時間データに影響を与えている要因(共変量)を調べることや生存曲線を予測するモデルを作ることができます.
主成分分析
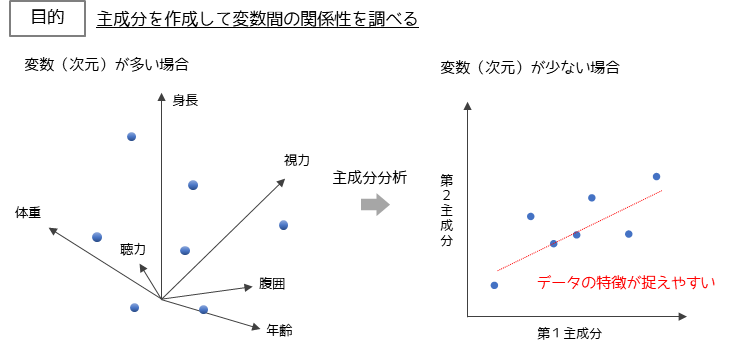
主成分分析は,多変量データを「要約」する手法になります.
多変量データは変数の数が増えるほどデータが特性を捉えることが難しくなります.そこで,多変量データから新しい指標(主成分)を合成してデータの特性を見やすくする手法が主成分分析になります.
感覚としては,多次元であったデータを少ない次元(上図では2次元)で表すといったイメージです.
主成分分析は目的変数が無い多変量解析で,全てのデータを説明変数として扱い総合的な指標を生み出します.
因子分析
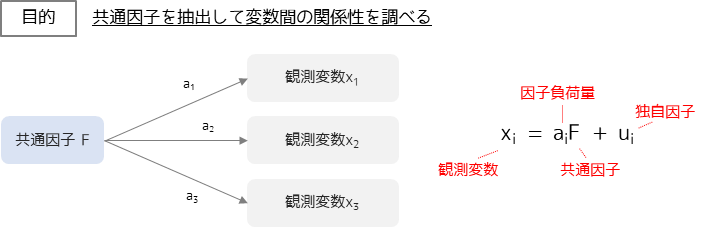
因子分析は主成分分析と類似した分析手法ですが,考え方や目的は大きく異なります.
因子分析では説明変数(観測変数)の背後にある共通因子(潜在変数)を抽出して,データ間の関連性を理解する手法です.
次元を少なくして多変量データの特性を見やすくするといった意味では,主成分分析と類似した手法と言えます.
共分散構造分析
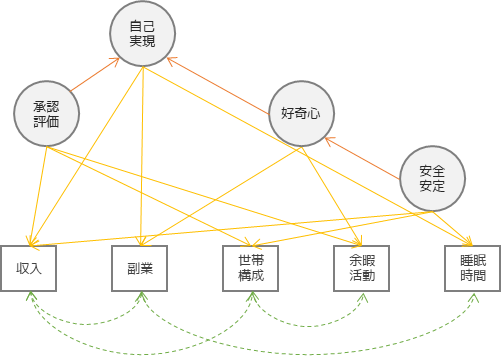
共分散構造分析(CSA;Covariance Structure Analysis)は,因子分析と重回帰分析を組み合わせたような分析手法です.因子分析では共通因子を見つけ出すということが可能でしたが,共分散構造分析では潜在変数(因子)間での関係性(赤矢印)についても調べることができます.
特に心理学の研究や,マーケティング分野でデータの背景にある関係性を調べるために用いられます.
クラスター分析

クラスター分析は,多変量データを分類してクラスター(集団)を作るための分析手法です.クラスターの作成方法によって様々な手法がありその総称をクラスター分析と言います.
クラスターを作成することで,出来上がったクラスターごとにデータを解釈することができます.
》階層クラスター分析の手順(Python)
》非階層クラスター分析の手順(Python)
コレスポンデンス分析
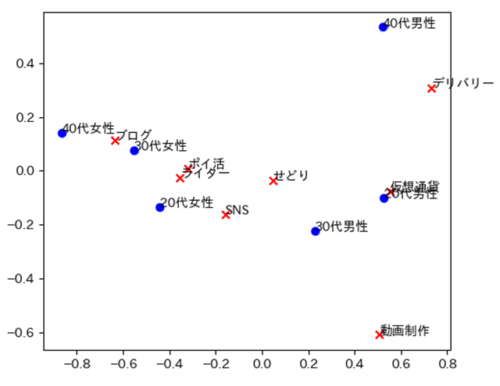
コレスポンデンス分析はカテゴリーデータの関連性を調べる手法です.
クロス集計表から散布図を作成することで,視覚的に変数間の関連性を判断することができます.
数量化Ⅲ類
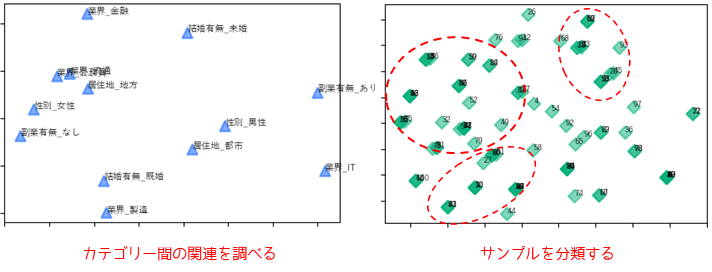
数量化Ⅲ類はカテゴリーデータに対して行う多変量解析です.複数変数のカテゴリー(要素)ごとに関連性を調べることができます.また,新しく合成した基準(軸)を用いて,サンプル(被験者)の分類を行うこともできます.
複数変数のカテゴリーデータに対して分析できるため,多重コレスポンデンス分析(多重対応分析)とも表現されます.
決定木
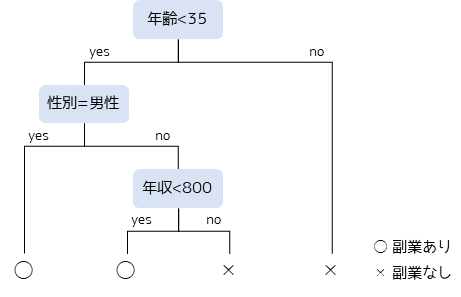
決定木(Decision Tree)とは機械学習の1つのアルゴリズムで,データの分類・予測を行うために使用されます.決定木はある条件に基づきデータを2分割して,さらにその結果に基づきデータを分割するという作業を繰り返すアルゴリズムです.
結果の解釈が容易であること,カテゴリーデータ・数量データの両方に対して行うことができるため多変量解析の中でも非常に便利な手法です.
補足① カテゴリーデータの分析方法
多変量解析は基本的には,数量データを分析するための手法になります.特に「要約」する手法である主成分分析やクラスター分析ではカテゴリーデータを扱うことができません.
カテゴリーデータの分析方法には,大きく3つの方法があります.
① ダミー変数
カテゴリーデータをダミー変数に変換することで,数量データとして扱うことができます.
例えば主成分分析で血液型というカテゴリーデータを扱いたい場合は,ダミー変数に変換して扱うことができます.重回帰分析においても一部の変数だけカテゴリーデータであった場合,ダミー変数に変換することで行うことができます.
② クロス集計表
カテゴリーデータの分析方法として最も一般的なのがクロス集計表になります.
多変量データをカテゴリ毎に度数で集計をして分析を行います.クロス集計表の分析方法としては,カイ二乗検定やオッズ比,コレスポンデンス分析があります.
③ 数量化理論
既に紹介した数量化Ⅱ類や数量化Ⅲ類も,カテゴリーデータを数量データのように分析するための手法です.
数量化Ⅱ類は重回帰分析のカテゴリーデータ版,数量化Ⅲ類は主成分分析のカテゴリーデータ版と考えるとイメージがしやすいかと思います.
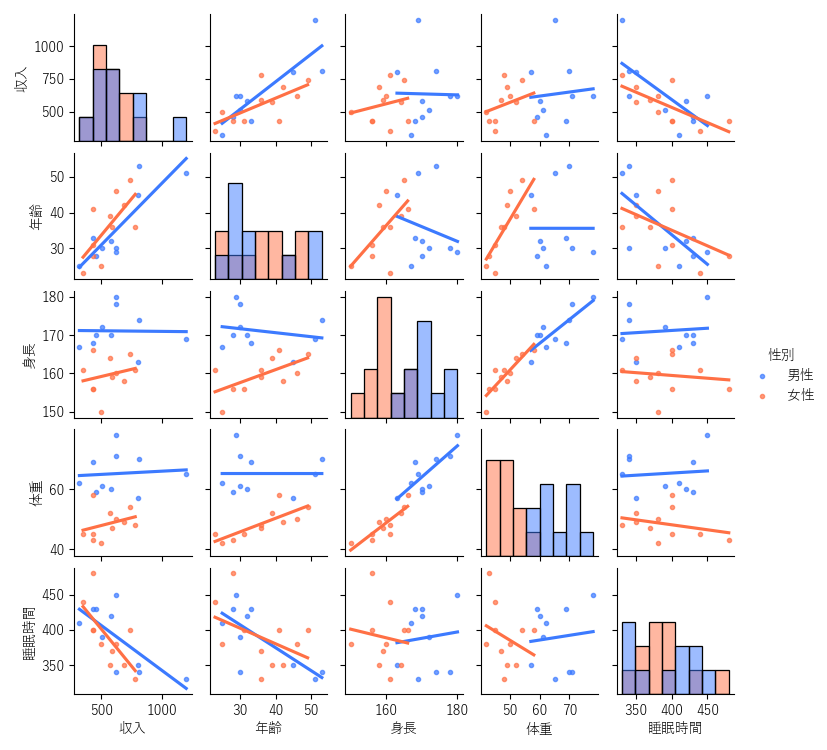
補足② 散布図行列(変数間の相関関係の把握)
多変量解析の各変数間の特徴を調べる,示すために散布図行列がよく用いられます.散布図行列は以下のように,全変数のペアで散布図を作成したグラフになります.
実際に多変量解析を行う前は,散布図行列を作らなくとも各変数の相関関係を調べて特徴を把握することは基本手順になります.(多重共線性の回避)