数量化Ⅲ類とは
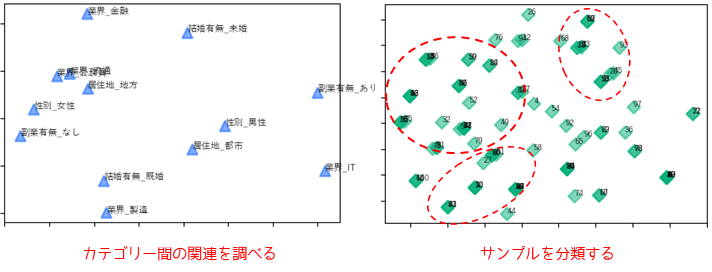
数量化Ⅲ類はカテゴリーデータ(質的変数)に対して行う多変量解析です.複数変数のカテゴリー(要素)ごとに関連性を調べることができます.また,新しく合成した基準(軸)を用いて,サンプル(被験者)の分類を行うこともできます.
数量データに対して行う主成分分析(PCA)とよく似た手法であり,多重コレスポンデンス(MCA)と同等の分析方法です.
数量化とは林知己夫先生によって開発された手法で,数値でないデータを数値化する手法になります.数量化を行うことでアンケートの調査結果などの分析を行うことができます.
数量化Ⅲ類の具体例
副業の実態を調査することを目的として,20代の社会人100人に対してアンケートを取り,副業有無に加えて属性情報を収集したとします.
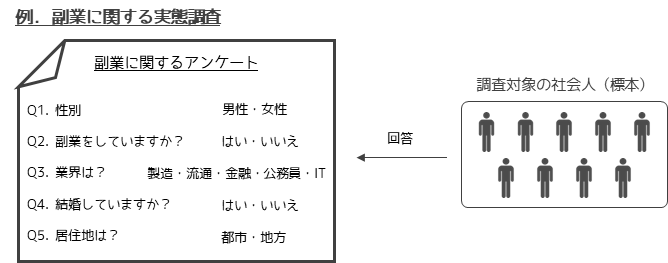
収集したサンプルデータは以下のようになります.

質問項目全てを分析対象の変数として,数量化Ⅲ類を行いカテゴリースコアを算出します.カテゴリースコアとは,特定のカテゴリが多次元空間上でどのように位置するかを示し,そのカテゴリがデータセット内の他のカテゴリとどのように関連しているかを理解するのに役立ちます.
合成変数として算出した軸1と軸2に対して,散布図を作成すると以下のようになります.
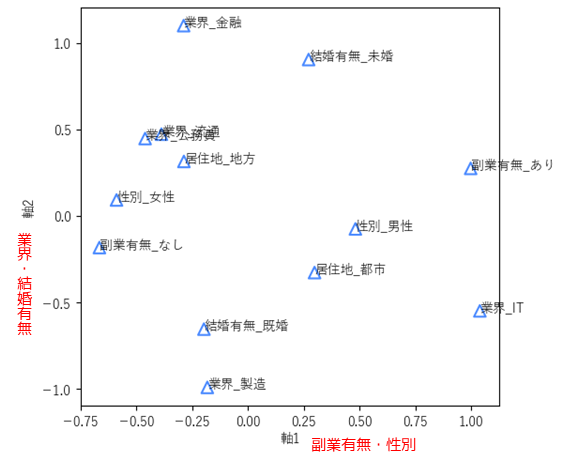
カテゴリースコアの分布から,軸1は主に”副業有無”と”性別”を考慮した変数であり,軸2は”業界”と”結婚有無”を主に考慮した変数であることがわかります(ネーミング).
プロット間の距離は関連度を示し,例えば”女性”と”副業なし”は距離が近いことから,「女性は副業を行わない傾向がある」と解釈することができます.
また,”既婚”と”製造”についても距離が近いことから「製造業の従事者は結婚している傾向がある」と解釈することができます.
次に合成変数に対して,サンプルデータを適合したサンプルスコアを算出します.算出した軸1と軸2に対して,散布図を作成すると以下のようになります.
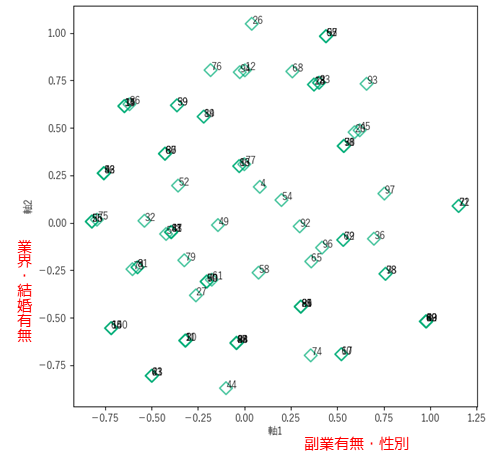
ラベルはサンプル番号となり,例えば散布図の右端にプロットされてるNo.22とNo.71(見にくいですが,,)の回答者は同じような属性を持つと判断することができます.
サンプルスコアは変数に対する各回答者の類似度を示すので,分布に偏りがあればそれらをクラスター(集団)として分類することもできます.
カテゴリー変数が2つの場合
2つのカテゴリー変数に対して,分析を行いたい場合はクロス集計を行います.
例えば”副業”と”業界”に対して分析を行う場合は,以下のようなクロス集計表を作成します.

クロス集計表から”IT”と”副業あり”の値が多いことから,「IT業界の人は副業を行う傾向がある」と解釈することができます.同様に「公務員は副業を行わない傾向がある」と解釈することができます(基本的には公務員は副業禁止なので,,).
コレスポンデンス分析を行うと,同様の傾向を図示することができます.
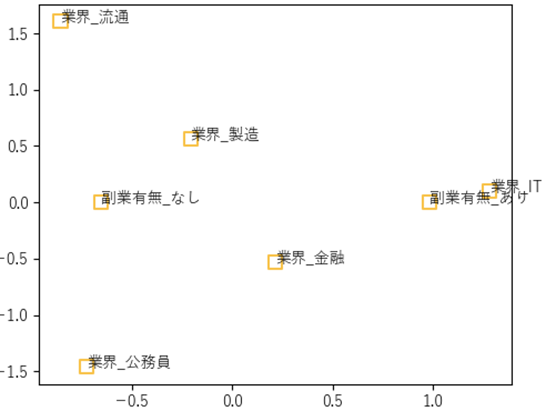
このようなクロス集計表を用いた分析は,数量化Ⅲ類の事前分析としても非常に有効です.
数量化Ⅲ類の実行方法
数量化Ⅲ類は非常に複雑な計算が必要なため,手計算やExcelを用いて行うことは難しいです.統計解析アプリStaatAppでは,本ページで紹介してるデータの解析やグラフ作成も全て実行可能です.
Staatでは数量化Ⅲ類用のStaatAppを470円という価格で販売しています.StaatAppとはPC用の統計解析アプリで,任意のデータを読み込みクリック操作だけで統計解析を行うため購入から数分で結果まで知ることができます.
》StaatAppで行う数量化Ⅲ類
》統計解析アプリStaatAppとは
補足① コレスポンデンス分析(対応分析)との違い
コレスポンデンス分析はカテゴリー変数が2つの場合行う分析手法です.数量化Ⅲ類において変数を2つにした場合と同等の分析になるので,コレスポンデンス分析の拡張版が数量化Ⅲ類と考えて問題ありません.
コレスポンデンス分析は対応分析と表記されることもあります.また,3つ以上の変数に対して行うコレスポンデンス分析を多重コレスポンデンス分析(多重対応分析)と表現することもあり,多重コレスポンデンスは数量化Ⅲ類と同等の分析方法になります.
補足② 数量化Ⅰ類・数量化Ⅱ類
数量化とはカテゴリーデータを数値データに変換して,数値データのように分析を行う手法です.数量化理論には数量化Ⅲ類の他に,数量化Ⅰ類や数量化Ⅱ類があります.
数量化Ⅰ類や数量化Ⅱ類は重回帰分析と類似した手法で,目的変数と説明変数に分けて分析を行います.数量化Ⅰ類は目的変数が数量データ(量的変数),説明変数がカテゴリーデータ(質的変数)の場合に用いられます.数量化Ⅱ類は目的変数・説明変数ともにカテゴリーデータである場合に用いられます.

数量化理論以外では,目的変数がカテゴリーデータで説明変数が数量データの場合はロジスティック回帰分析がよく使われます.










