多変量解析の1つである主成分分析について,図と例題を用いて徹底解説しています.
主成分分析の手順や結果の見方,因子分析との違いについても解説しています.
主成分分析とは
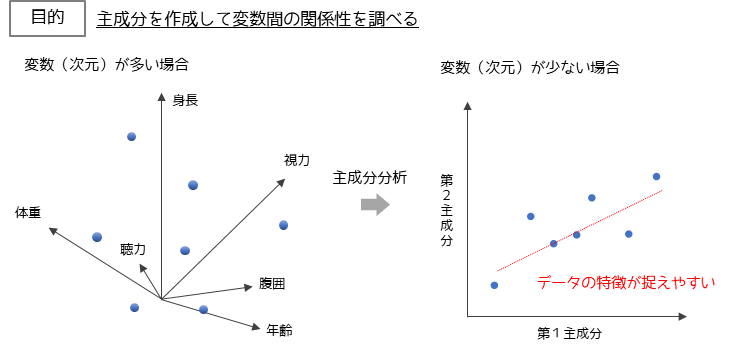
主成分分析とは多数の変数に含まれている情報を要約して,少数の変数で表す手法です.
変数が多い場合データの特徴が直感的に分かりづらいですが,変数(次元)を少なくすることでデータの特徴が捉えやすくなります.2つの主成分に要約した場合は,平面の散布図としてデータを見ることができます.
主成分分析の活用例
主成分分析の具体的な活用例を紹介します.
社会人21人に対して,アンケート調査を行い以下のようなデータを作成したとします.

調査項目(観測変数)は以下の通りです.
x1:副業の有無
x2:年収
x3:性別
x4:年齢
x5:結婚の有無
主成分分析を行い,x2とx4が強く影響している主成分(PC1)を作成したとします.

作成した主成分は観測変数x2とx4を総合的に示した指標であることがわかります.
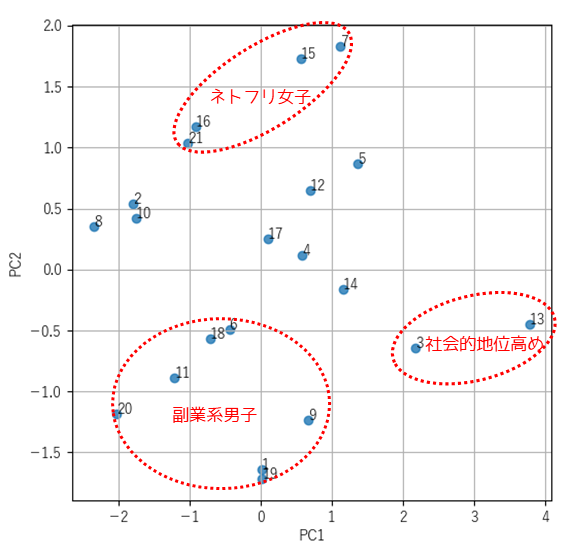
求めた主成分に対してネーミングを行うことで,主成分得点から以下のように回答者の属性を捉えることもできます.詳しくは「結果の解釈」で解説しています.
主成分分析の手順
主成分分析は以下の手順で行います.
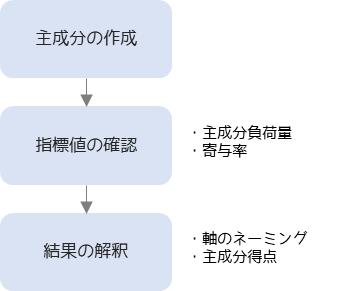
主成分はデータの分散が最大になる方向を示すように作成します.主成分は元データの変数分だけ作成することができ,主成分の分散が大きいものから順に第1主成分,第2主成分,…と言います.
分析結果として作成した主成分・観測変数ごとの主成分負荷量・寄与率を確認します.累積寄与率が80%以上を目安に主成分を選択します.
選択した主成分がどのような意味を持つのか,主成分負荷量から考えます(軸のネーミング).選択した主成分を軸として主成分得点プロットした散布図から,データの特徴を解釈します.
主成分分析の実行方法
主成分分析は非常に複雑な計算が必要なため,手計算やExcelを用いて行うことは難しいです.主成分分析は一般的にRやPython,有料統計解析ソフトを用いて行われます.
本サイトでは2つの方法を紹介しています.
① Pythonを用いた方法
Pythonを用いた方法を,初めてプログラミングを行う方でもわかるように解説しています.
》Pythonを用いた統計解析
》Pythonを用いた主成分分析
② 統計解析アプリ(StaatApp)を用いた方法
StaatAppとは任意のデータを数クリックだけで統計解析ができるPC用アプリです.Rと比較しても簡単に分析を行うことができるので,今すぐ結果を知りたい方におすすめです.
》StaatAppで行う主成分分析
》統計解析アプリStaatAppとは
各指標値の意味と解釈
主成分分析の実行結果は以下のように出力されます.活用例のデータを実際に計算する際は,ダミー変数への変換が必要です.

① 主成分負荷量
主成分負荷量とは各主成分と各変数の関連性の大きさになります.各主成分に関係性が深い変数ほど絶対値が大きくなり-1から1の間の値を取ります.
第1主成分に対して主成分負荷量が高い変数は,x2とx4であることがわかります.
② 寄与率・累積寄与率
寄与率とは,各主成分がどれだけの情報を説明できているかという指標になります.
第1主成分の寄与率は約45%であり,累積寄与率から第3主成分までで約83%の情報を説明できているということが分かります.これより,第4主成分以下はあまり寄与していないことがわかります.
結果の解釈(軸のネーミング)
主成分分析の結果は各主成分に名前をつける(軸のネーミング)ことで解釈を行います.各主成分との相関の度合いを表す主成分負荷量を見ることで主成分に名前を付けます.
活用例では主成分負荷量から以下のことがわかります.
■第1因子が強く影響している変数
x2:年収
x4:年齢
■第2因子が強く影響している変数
x1:副業の有無(負の値なので正の方向は副業無し)
x3:性別(負の値なので正の方向は女性)
影響を与えている変数の共通点から,第1主成分は”社会的地位”,第2主成分は”Netflixをよく見る女性(副業をしていない女性)”とネーミングすることができます.
第1主成分と第2主成分に名前を付けたことで,第1主成分(PC1)と第2主成分(PC2)に対する主成分得点を示した散布図は以下のように解釈することができます.

散布図の左下に位置する回答者は,副業を行っている男性かつ社会的地位がそれほど高くないと捉えることができます.
補足① 因子分析との違い
因子分析は主成分分析と類似した分析手法ですが,考え方や目的は大きく異なります.
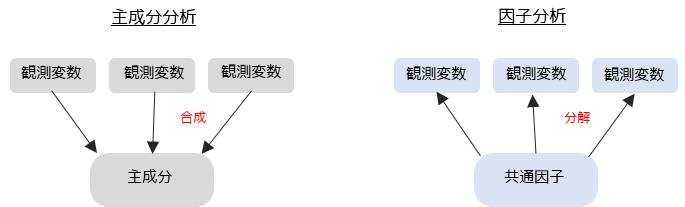
因子分析は多変量解析の中でも,観測変数に影響を与えている共通因子を抽出するために用います.観測変数を要約する主成分分析とは,正反対の分析方法になります.
補足② 主成分分析を行う前提条件
主成分分析は,多変量解析の中でも扱うデータの前提条件が非常に少ない分析手法です.しかし,以下2つの条件については注意してください.
① 量的変数
主成分分析の対象データは量的変数である必要があります.アンケートの調査結果などでカテゴリー変数を含んでいるデータを扱う場合は,ダミー変数を用いる必要があります.
② 変数間(項目間)に逆相関がない
変数間に逆相関があるデータは,主成分分析を行うことができません.
変数間に逆相関がある場合,特定の項目の値が高いほど逆相関がある項目の値が低くなります.この場合,主成分分析で求めた各主成分は”総合力”といった意味を持たなくなります.










