一般化線形混合モデルとは
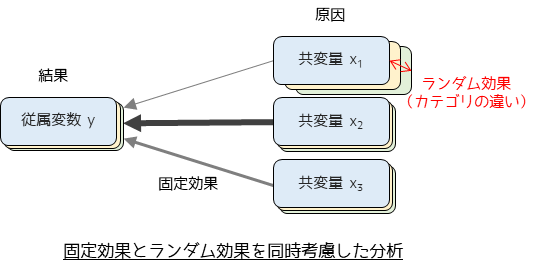
一般化線形混合モデル(Generalized Linear Mixed Models; GLMM)は,統計モデルの一つで,固定効果とランダム効果の両方を考慮します.固定効果はすべての個体やグループに共通する効果を示し,ランダム効果は個体やグループ間のランダムな変動を捉えます.様々なデータに合わせて柔軟なモデルを作成できるため使用場面は多岐にわたりますが,特に繰り返し測定データや階層的なデータ構造を持つデータの分析に適しています.
例えば,社会人の年収と年齢の関係について考えてみます.終身雇用制度においては年収と年齢には相関関係があり,線形回帰モデルで表すことができます.
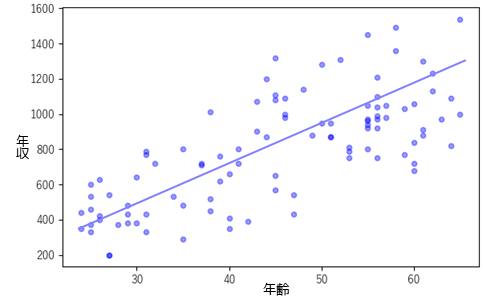
ここで業界ごとに給与水準に差がある場合を考えます.線形回帰モデルでは業界の違いを考慮することができませんが,一般化線形混合モデルでは業界の違い(ランダム効果)を考慮することができます.
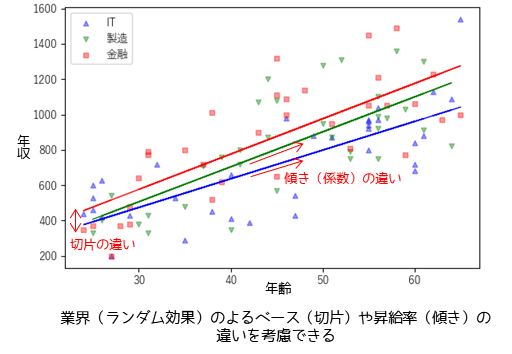
一般化線形混合モデルでは,ランダム切片(ベースの差)やランダム係数(昇給率の差)をモデルに含めることで,従属変数(年収)に対する固定効果(年齢)とランダム効果(業界)の影響を調べることができます.
このページではGLMMを一般化線形混合モデルと表現しますが,混合効果モデルと表現されることもあります.
何がわかるのか?(分析の目的)
一般化線形混合モデルでは主に2つの目的で,使用される分析手法です.従属変数への影響度については重回帰分析,固定値効果内の差については分散分析のような分析結果を得ることができます.
従属変数への影響度
各共変量(説明変数)が従属変数(目的変数)にどれだけ影響しているかを調べることができます.
年収の例では,年齢という共変量に加えて通勤時間や世帯人数を含めるとします.業界による差を考慮した上で,どの共変量がどれだけ従属変数に影響を与えているか調べることができます.
固定効果内の差(仮説検定)
固定効果の値ごとに差があるかを調べることができます.特にカテゴリーデータの差を調べるために用いられます.
年収の例では,年齢という共変量に加えて性別というカテゴリーデータを含めるとします.業界による差を考慮した上で,性別の差によって年収に差があるかをp値を用いて調べることができます.
どのようなデータに使うか?
一般化線形混合モデルは様々なデータに対応できますが,特にネストされている場合と反復測定された場合のデータの分析に使用されます.
ネストされている場合

ネストとは例のように大きなグループの中に,さらにグループがあるような構造を持つデータになります.
年収の例では,業界というグループの中の個人というグループに年齢などの属性情報は所属すると考えると,ネストされたデータと言えます.
反復測定の場合
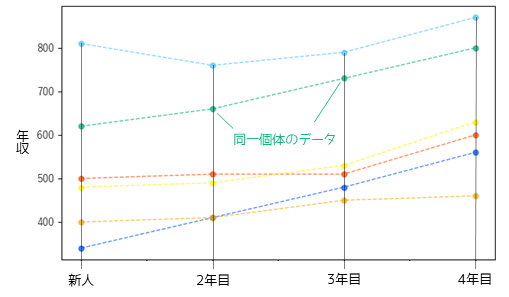
反復測定とは同一個体から繰り返しデータを取得することになります.仮説検定では”対応のある”といった表現をすることもあります.
社会人の1年ごとの年収の推移データは,同一の個人から繰り返しデータを得ているため反復測定されたデータになります.
反復測定データに対する一般化線形混合モデルを用いた分析については,以下の動画で詳しく解説されています.特に医療分野で用いたい方は必見です.
ダミー変数を含む重回帰分析とどう異なるのか?
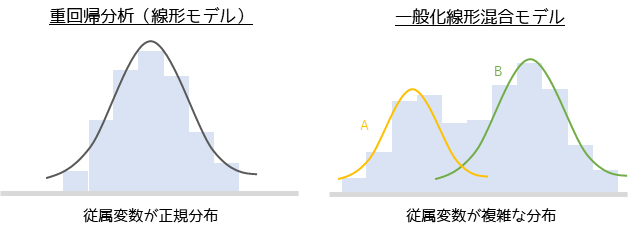
カテゴリーや個人ごとの影響を考慮した分析を行なう場合に思いつくのが,カテゴリーデータをダミー変数に変換して重回帰分析を行なうことです.
重回帰分析は線形モデルに分類され,線形モデルの従属変数は正規分布に従うという仮定が必要になります.実際にカテゴリーや個人の差による影響が見られる場合,従属変数が1つの正規分布に従うということはほとんどありません.
一般化線形混合モデルであれば,従属変数の確率分布をランダム効果に設定してカテゴリー・個人ごとの分布の組み合わせとして考えることができます.そのため,より現実的なデータに合わせた分析手法は一般化線形混合モデルになります.
ダミー変数として重回帰分析を行った場合,パラメータ(説明変数)の数が増えすぎるという問題も発生します.例えばカテゴリー数が6であった場合,ダミー変数は5となりパラメータの数が非常に大きくなってしまいます.パラメータ数が多いと過学習という問題が発生します.
ランダム効果と固定効果
ランダム効果(Random Effects)は,個体やグループ間のランダムな変動を表す効果で変動効果と表現される場合もあります.分析を行なう場合は,ネストされているデータであれば所属を表すカテゴリーが,反復測定されたデータであれば同一サンプルを示すIDなどをランダム効果として設定します.
分析結果として,ランダム効果は特定のグループやカテゴリの平均からの偏差を知ることができます.
固定効果(Fixed Effects)はデータ全体にわたって一定の効果や影響を持つと考えられる変数の効果です.分析を行なう場合は調べたい影響を示すデータや,比較する時点を示すラベルデータを設定します.
一般化線形混合モデルを用いた分析を行なう場合,従属変数とランダム効果,固定効果に変数を割り当てます.ランダム効果は所属するカテゴリーやIDを設定することが多いですが,固定効果に設定する場合もあります.ランダム効果と固定効果を選択する上で考えることは,知りたい結果になります.「何がわかるのか」で説明したように,基本的には固定効果に設定した変数について,様々な解釈を行なうことができるので,例えば所属するグループによる差を調べたい場合は,固定効果として分析を行います.
従属変数(目的変数)と共変量(説明変数)の選び方については,以下のページをご覧ください.
▷ 説明変数と目的変数
従属変数の確率分布
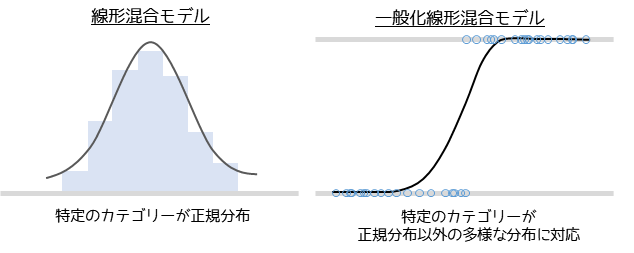
一般化線形混合モデルでは従属変数の特性に合わせた確率分布を選択して,モデルを構築します.
ランダム効果の設定したカテゴリー毎の従属変数が連続的で正規分布に従う場合は,正規分布を用いてモデルを構築します.正規分布を用いたモデルは線形混合モデル(Linear Mixed Models; LMM)とも表現され,一般化線形混合モデルの1種になります.
正規分布以外では,従属変数が2値データである場合に用いる二項分布や,カウントデータである場合に用いるポアソン分布,累積データである場合に用いるガンマ分布があります.
線形混合モデルと比較して様々な従属変数に対して用いることができるのが,一般化線形混合モデルになります.
既に説明したように,一般化線形混合モデルはランダム効果ごとの分布を組み合わせて考えることができます.そのため,分析に用いる従属変数自体が特定の確率分布に従う必要はありません.
ランダム切片とランダム係数
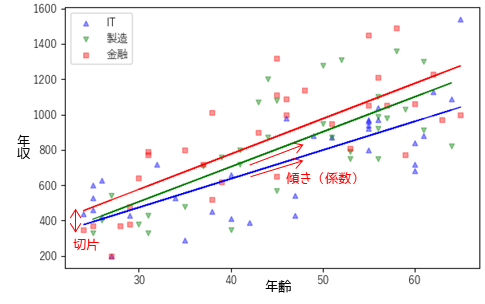
一般化線形混合モデルでは,ランダム効果を用いることでカテゴリーの違いを考慮することができます.実際にモデルを構築する際には,ランダム効果はランダム切片やランダム係数として分析を行います.
ランダム切片を含むモデルはカテゴリーごとの平均的な値の差を考慮することができます.年収の例では,業界ごとのベースの違いを考慮したい場合にランダム切片を用います.
ランダム係数を含むモデルはカテゴリーごとの変化率の差を考慮することができます.年収の例では,業界ごとの昇給率の差を考慮することができます.
一般化線形混合モデルの最も単純かつ使用されるモデルは,ランダム切片のみ含むモデルです.ランダム切片のみでは不十分な場合に,ランダム係数をモデルに追加します.ランダム係数のみ使用した分析が行われることはほとんどありません.
共変量が複数ある場合,2次元ではなくなるため散布図を用いてモデルの構造を考えることが難しいです.そのような場合は,複数パターン(ランダム切片のみやランダム切片+ランダム係数など)でモデルを構築した後に,尤度比検定を行い最適なモデルを選択します.
尤度比検定は,ネステッドモデル(一方のモデルがもう一方のモデルの特殊ケースであるモデル)のペアを比較する際に特に有効です.ランダム切片のみモデル(簡略モデル)とランダム切片とランダム係数を含むモデル(フルモデル)の間の適合度を比較することで,簡略モデルがフルモデルと同じくらいの情報を持っているかどうかを評価することができます.
一般化線形混合モデルを行なう方法
一般化線形混合モデルを用いた分析は計算方法が複雑なため,Excelなどの手計算で行うことは難しいです.基本的にはRやPythonなどのプログラミング言語を用いて行う必要があります.
統計解析アプリStaatAppでは一般化線形混合モデルを,プログラミングを行わずクリック操作だけで行なうことができます.様々なデータやモデル構造にも対応しています.
詳細は以下のページをご覧ください.
》統計解析アプリStaatApp
》StaatAppを用いた一般化線形混合モデル
参考書籍
線形モデルや一般化線形混合モデルについては通称”みどり本”と呼ばれる名著があります.数式だけでなく,具体例を用いた非常にわかりやすく解説されているのでより詳細に知りたい方は必読の本です.
データ解析のための統計モデリング入門 一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学)










