StaatAppでロジスティック回帰分析を行う方法を紹介します.SaatAppではCSVファイルやExcelファイルを読み込み,クリック操作だけでロジスティック回帰分析を行うことができます.
StaatAppについては以下をご覧ください.
アプリの基本操作
StaatApp基本操作(データの入出力など)は以下のページで解説しています.
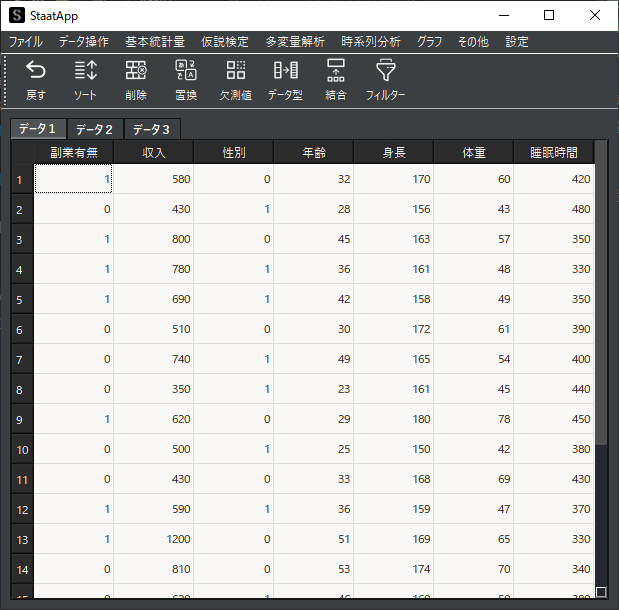
分析例として用いるサンプルデータは以下のようになります.”副業有無”と”性別”はダミー変数となっていますが,置換機能を用いてダミー変数に変換することも可能です.(副業有→”1″,女性→1″)
ロジスティック回帰分析の実行(モデルの作成)
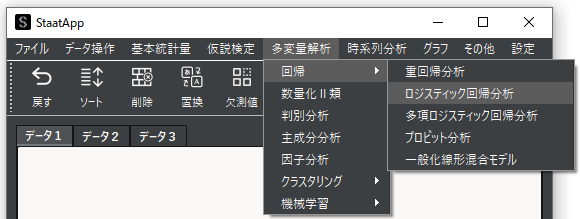
メニューバーから「多変量解析」→「回帰」→「ロジスティック回帰分析」を選択してロジスティック回帰分析用ウィンドウを表示します.
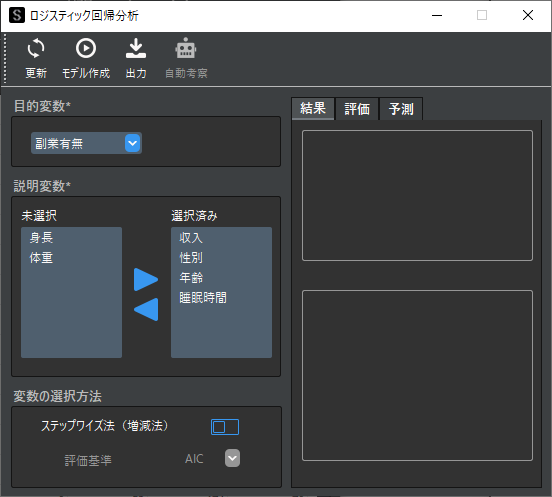
ロジスティック回帰分析用ウィンドウが表示されたら,目的変数と説明変数の設定を行います.
ダミー変数を説明変数に選択する際は,多重共線性の問題を回避するために”1列分”を除いて選択します.
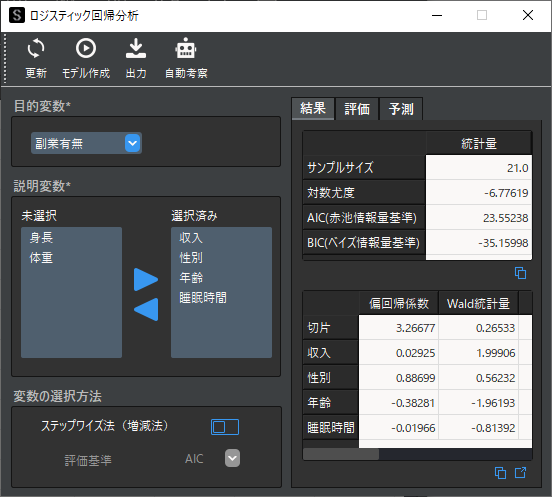
設定項目に入力が完了したら,ツールバーの「モデル作成」ボタンをクリックします.画面右側の「解析結果」にロジスティック回帰分析の結果が出力されます.
※ 説明変数に対してサンプルサイズが小さすぎると,モデルが作成できず結果は出力されません.
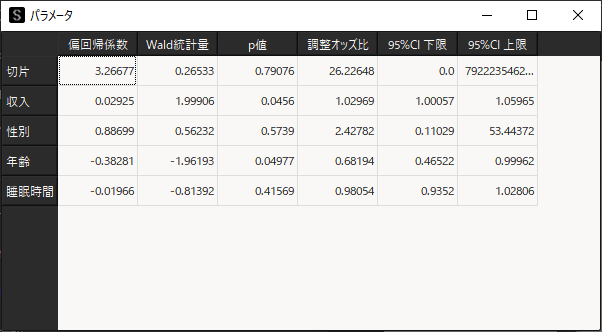
パラメータはポップアップボタンをクリックすることで以下のように表示することもできます.
ステップワイズ法(応用)
選択した説明変数からステップワイズ法(増減法)で変数を自動選択する場合は,「変数の選択方法」のオプションで,ステップワイズ法をクリックしてから「モデルの作成」を行います.
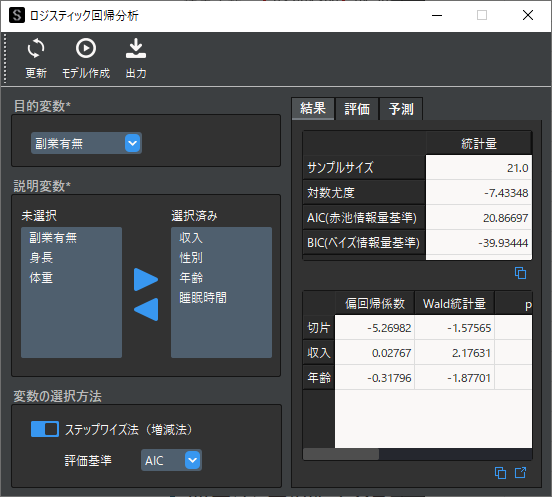
ステップワイズ法で使用するモデルの評価基準は,赤池情報量規準(AIC)もしくはベイズ情報量規準(BIC)から選択可能です.
予測精度の評価(応用)
作成したモデルに対して,予測精度の評価を行う場合は「評価」タブで行います.事前にテストデータをモデル作成とは別のデータに入力しておき,「テストデータの選択」で対象のデータを選択します.
「算出」ボタンをクリックすると,以下のように各評価指標と混合行列が表示されます.
※ テストデータには説明変数で選択した変数名(列名)を含む必要があります.
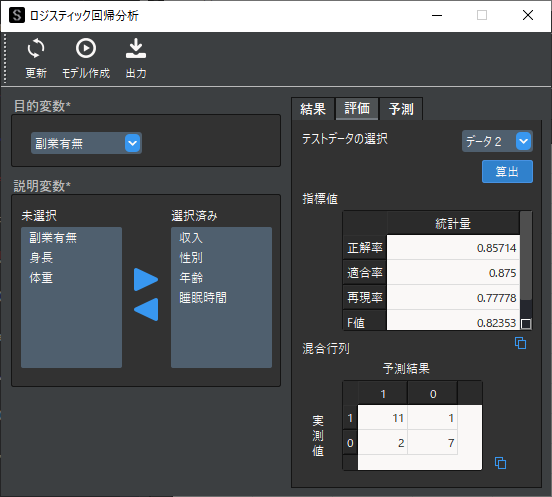
分類問題の評価指標と混合行列は以下のページで解説しています.
予測値の算出(応用)
作成したモデルを用いて予測値の算出を行います.「予測」タブから「予測用データの選択」を行い「算出」ボタンをクリックします.
※ 予測用データには説明変数で選択した変数名(列名)を含む必要があります.
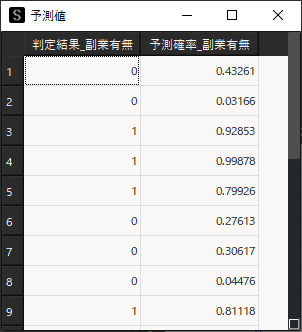
予測用データに対して,判定結果と予測確率が算出されます.
自動考察(有料)
ロジスティック回帰分析の解析結果について自動考察を行なうと,モデルの適合度と説明変数ごとの統計量について,以下のような考察結果を得ることができます.
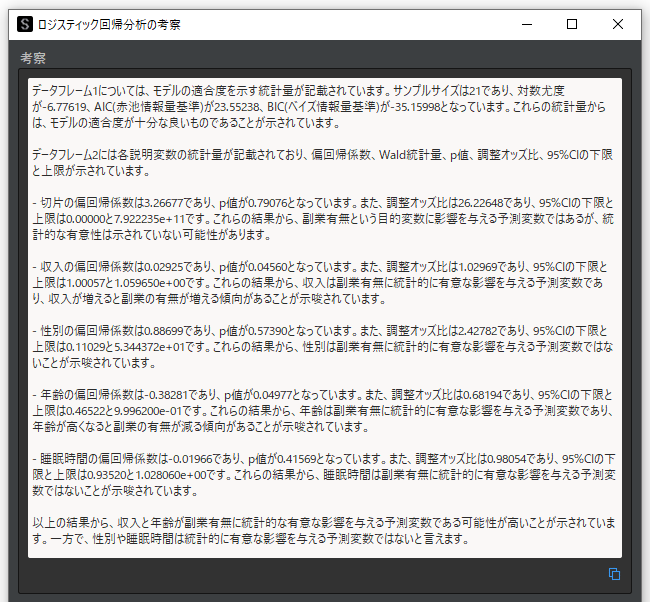
説明変数や統計量についてさらに詳しく知りたい場合は,追加解説機能で回答を得ることができます.以下は”収入”について,追加解説を出力した例になります.
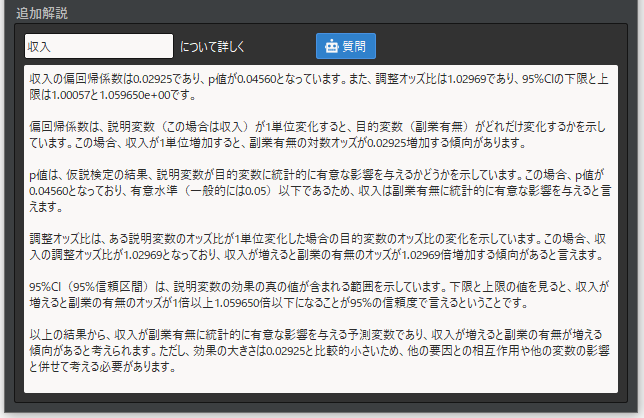
補足① 結果の見方
ロジスティック回帰分析の結果で見るべきポイントは4つになります.
① 対数尤度
尤度(ゆうど)とは尤(もっと)もらしさを示す指標になります.対数尤度は値が大きいほど推定した回帰モデルの当てはまり良いことを意味します.
今回のような説明変数の組み合わせが1つの場合は見る必要はありません.説明変数の候補となるデータが他にもあり複数パターンで回帰モデルを推定した際に,対数尤度が最も大きい組み合わせが最も良い回帰モデルであると言えます.
② 偏回帰係数
偏回帰係数は0の場合は,その説明変数は推定した回帰モデルに影響を与えないということを意味します.値が正の場合は確率を上げる方向に,負の場合は確率を下げる方向に影響を与えます.
「収入」という説明変数は正の値であるため,収入が多いほど副業をしている確率が上がることを意味します.「年齢」は負の値であるので年齢が上がるほど,副業をしている確率が下がることを意味します.
※「切片」は回帰モデルの定数項になります.
③ Wald統計量
Wald統計量の絶対値が大きいほど,目的変数に影響を与えているということを意味します.
Wald統計量の絶対値が最も大きいのは「収入」であるので,年収の多さが副業の有無に最も影響を与えていると言えます.
④ p値
p値とは偏回帰係数のWald統計量についてのp値になります.p値が有意水準を下回ればその説明変数は有意な偏回帰係数であることが言えます.
統計学では一般的に有意水準α=0.05とすることが多いです.有意水準α=0.05とは,実際に関連性がない場合でも関連性が存在すると結論付けるリスクが5%であることを意味します.
有意水準α=0.05とすると,収入と年齢のみが統計的に有意であり目的変数に関連性があると言えます.
⑤ 調整オッズ比と95%信頼区間(95% CI)
調整オッズ比は偏回帰係数の自然対数として求められます.調整オッズ比は値が1未満の場合,目的変数に対して負の方向に,1以上の場合は正の方向に影響することを意味します.
オッズ比の95%信頼区間は下限値と上限値が”1”を跨がない場合,その説明変数は統計学的に有意であることを示します.
解析結果からはp値と同じ説明変数が有意になっていることがわかります.
補足② 統計アプリStaatAppとは
StaatAppは計算仮定が複雑な解析手法を,誰でも手軽に素早く行なうことができるアプリです.
無料版では以下の機能が使用可能です.
・データ操作機能
・基本統計量
・パラメトリック検定
・正規性の確認(Q-Qプロットの作成,コルモゴロフ・スミルノフ検定,シャピロ・ウィルク検定)
・ロジスティック回帰分析
・決定木分析
・時系列分析
・グラフ作成
ロジスティック回帰分析以外の解析手法の使い方は以下のページで解説しています.
StaatAppのダウンロード及び詳細は以下のページをお読みください.
補足③ アプリの仕様について
アプリではPythonのScipyライブラリに含まれる,statsmodelsモジュールを用いてロジスティック回帰分析を行っています.statsmodelsはPythonで統計解析を行なう際に最も一般的なモジュールです.一般化線形モデルを作成する際に,確立分布は二項分布,リンク関数はロジット関数を用いています.
アプリを用いずに,Pythonでプログラムを記述して行う方法は以下の記事で紹介しています.
以下の公式ドキュメントに詳細な仕様が記載されています.
補足④ ロジスティック回帰分析とは
ロジスティック回帰分析とは,複数の要因(説明変数)から結果(目的変数)が起きる確率を説明・予測する統計的手法になります.
ロジスティック回帰分析と似た手法として,重回帰分析があります.重回帰分析との違いは目的変数になります.ロジスティック回帰分析では目的変数が”Yes/No”のような2つの値しか取らない場合に用いることができます.
目的変数が量的変数である場合は,重回帰分析を行います.
その他の多変量解析については,以下のページで詳しく解説しています.










