パラメトリック検定とノンパラメトリック検定
パラメトリック検定とは,母集団が確率分布に従っているという仮定のもとで行う検定方法です.
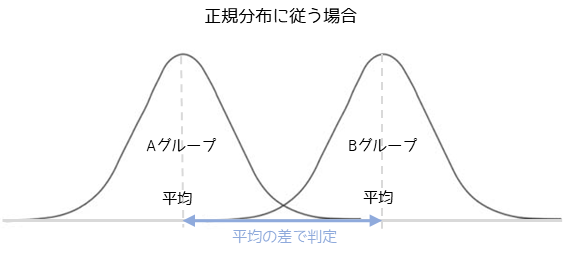
母集団が正規分布に従う場合,グループ間の平均値の差で母集団の差を判定します.代表的な手法として,t検定や分散分析があります.
ノンパラメトリック検定とは,母集団が確率分布に従っているという前提条件がいらない検定方法です.
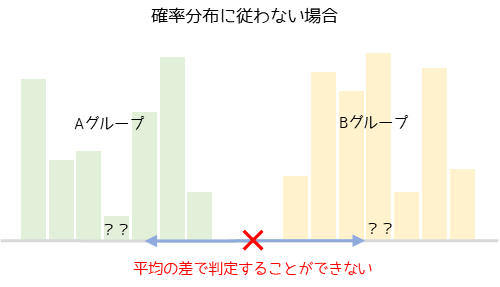
母集団がいづれの確率分布にも従わない場合,パラメトリック検定における平均値のように差を判定する基準値がありません.
母集団の分布を用いず,間接的に結果が起きる確率を計算する手法がノンパラメトリック検定になります.どのようなデータに対しても用いることができるため,非常に便利な検定方法です.
t検定などのパラメトリック検定を優先的に用いたいが,データの正規性に少しでも疑問がある場合は,ノンパラメトリック検定も併用で行うことをおすすめします.ノンパラメトリック検定でも,有意と判断されればより信頼性の高い結果となります.
ノンパラメトリックが有効なデータ
ノンパラメトリック検定を使うべき(=パラメトリック検定を使うべきでない)データについて3つ紹介します.
① 質的変数の場合
質的変数とは,職種や性別,成績といったカテゴリーデータ(名義尺度)や順序データ(順序尺度)になります.リッカート尺度を用いたアンケートの回答結果などもデータになります.
質的変数は値が確率変数ではないため,母集団は確率分布に従いません.(質的変数では平均値なども求めることはできません.)
② 外れ値がある場合
外れ値とは,データ群から極端な値を取るデータです.
外れ値がある場合にt検定を行うと,明らかに有意差がありそうなデータであっても有意差が出ないことがあります.
仮説検定を行う前に外れ値を対象のデータから除いてしまうことは統計学的にNGなため,ノンパラメトリック検定を行います.
ノンパラメトリック検定は外れ値に対しても検出力が高い検定方法です.
③ サンプルサイズが小さい場合
サンプルサイズが小さい場合,母集団が確立分布に従わない可能性が高いです.サンプルサイズが30以下(2群合わせて60以下)の場合は,ノンパラメトリック検定を行なうことが多いです.(中心極限定理)
しかし,サンプルサイズが小さいから必ずノンパラメトリック検定を行うという考え方は正しくありません.
ノンパラメトリック検定の選び方
ノンパラメトリック検定の選び方は,以下のフローチャートになります.
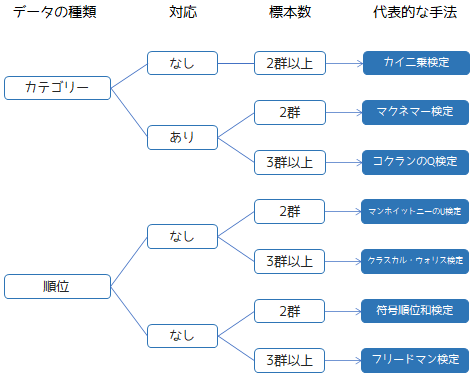
ノンパラメトリック検定を選ぶ際に必要な観点は以下の3つになります.
ノンパラメトリック検定一覧
ノンパラメトリック検定には,どのような検定手法があるか紹介します.
主なノンパラメトリック検定は以下のようになります.手法ごとの詳しい手順については,リンク先のページで解説しています.
|
名称
|
グループ数 | 対応 | データ | パラメトリック版 |
| カイ二乗検定 | 複数 | なし | カテゴリー | 対応のない多群の比率の差の検定 |
| 正確確率検定 | 2 | なし | カテゴリー | 対応のない2群の比率の差の検定(小標本) |
| マクネマー検定 | 2 | あり | カテゴリー | 対応のある2群の比率の差の検定 |
| コクランのQ検定 | 複数 | あり | カテゴリー | 対応のある一元配置分散分析 |
| マンホイットニーのU検定 | 2 | なし | 量的・順位 | 対応のないt検定 |
| ブルンナー・ムンチェル検定 | 2 | なし | 量的・順位 | ウェルチのt検定 |
| ウィルコクソンの符号順位検定 | 2 | あり | 量的・順位 | 対応のあるt検定 |
| クラスカル・ウォリス検定 | 複数 | なし | 量的・順位 | 対応のない一元配置分散分析 |
| フリードマン検定 | 複数 | あり | 量的・順位 | 対応のある一元配置分散分析 |
| スティール・ドゥワス検定 | 複数 | なし | 量的・順位 | テューキー法 |
※ グループ数:扱うデータのグループ数.複数であれば2グループ以上のデータに対して検定を行えます.
※ 対応:扱うデータが対応のある場合,もしくは対応のない場合です.
※ パラメトリック版:類似するパラメトリック手法です.
クロス集計表の代表的な分析手法であるカイ二乗検定は,カテゴリーデータを対象に検定を行うことができます.2群以上のデータを対象に検定を行うことができます.
t検定のノンパラメトリック版としては,マンホイットニーU検定やウィルコクソンの符号順位検定があります.順序尺度のデータを順位データに変換することで,分布の重なり具合を示す統計量を計算します.
3群以上のノンパラメトリック検定としては,クラスカル・ウォリス検定やフリードマン検定,スティール・ドゥワス検定があります.スティール・ドゥワス検定ではどの群間で差があるかを判定することができます.
統計解析アプリStaatApp
StaatAppとは任意のデータをマウス操作だけで統計解析ができるPC用アプリです.Rと比較しても簡単に分析を行うことができるので,今すぐ結果を知りたい方やExcelなどで計算ミスをしたくない方におすすめです.
StaatAppでは,以下のノンパラメトリック検定が実行可能です.
・マンホイットニーのU検定
・ブルンナー・ムンチェル検定
・ウィルコクソンの符号順位検定
・クラスカル・ウォリス検定
・フリードマン検定
・スティール・ドゥワス検定
・カイ二乗検定
・フィッシャーの正確確率検定










