カイ二乗検定(独立性の検定)とは
独立性の検定とは標本が十分に大きくない場合に行う,母比率の差の検定です.検定統計量はカイ二乗分布に従います.
以下の図が独立性の検定の考え方になります.社会人65人に対する調査結果の例です.
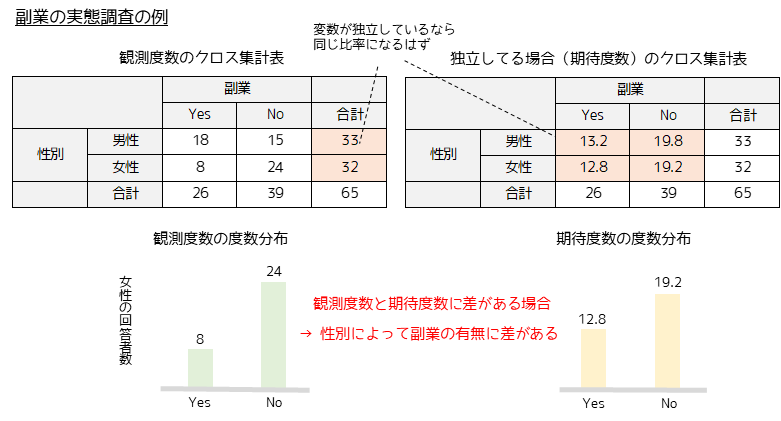
独立性の検定はクロス集計表の表側(性別)と表頭(副業有無)が関連しているのか,独立しているのかを判定する手法です.回答結果である観測度数と表側の横計の割合から求められる期待度数を用いて,検定統計量を求めます.
検定統計量は観測度数と期待度数に差があるほど大きくなり,カイ二乗分布の限界値(上限)より大きい場合に表側と表頭に関連性がある(独立していない)と判定します.
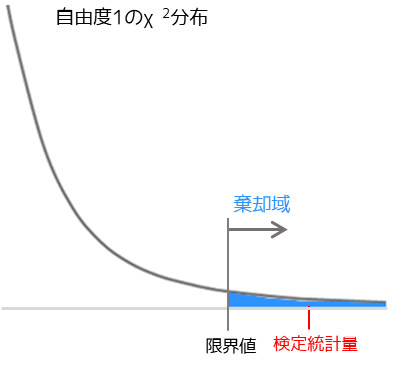
具体例では「性別と副業有無に関連性がある」=「性別によって副業有無に差がある」といった結論になります.
独立性の検定の手順
独立性の検定は以下の手順で行います.
① クロス集計表の作成
クロス集計表を作成します.
② 仮説の設定
帰無仮説は「クロス集計表の表側と表頭は独立している」,対立仮説は「クロス集計表の表側と表頭は独立していない」として設定します.
③ 有意水準の決定
有意水準α=0.05または0.01として設定します.一般的にはα=0.05で設定されます.
④ 検定統計量の算出
クロス集計表から検定統計量求めます.
⑤ p値の算出
検定統計量からp値を算出します.Excelでは直接p値を求めることができます.
⑥ 有意差判定
・p値<有意水準であれば,帰無仮説は棄却されて対立仮説を採択 → 「クロス集計表の表側と表頭は関連性がある(独立していない)」
・p値\(\geq\)有意水準であれば,帰無仮説は棄却されない → 「クロス集計表の表側と表頭は関連性があるとは言えない(独立していないとは言えない)」
仮説検定の考え方や用語については,以下のページで解説しています.
検定結果を間違いたくない方へ
Excelを用いた計算方法より簡単・正確に,カイ二乗検定の検定結果を調べることができる統計解析アプリStaatAppを販売しております.
StaatAppではカイ二乗検定以外にも,様々なクロス集計表の分析・仮説検定をマウス操作だけで実行することができます.詳細は以下のページをお読みください.
》StaatAppで行うクロス集計表の分析
》統計解析アプリStaatApp
例題で用いるデータと仮説の設定
例題では以下のサンプルデータを用います.社会人65人に対して副業の有無を調査した例です.
| No. | 性別 | 副業 |
|---|---|---|
| 1 | 女性 | してない |
| 2 | 男性 | してる |
| 3 | 女性 | してない |
| 4 | 女性 | してない |
| 5 | 男性 | してない |
| 6 | 女性 | してる |
| 7 | 女性 | してない |
| 8 | 女性 | してない |
| 9 | 女性 | してない |
| 10 | 女性 | してない |
| 11 | 男性 | してる |
| 12 | 女性 | してない |
| 13 | 男性 | してない |
| 14 | 女性 | してない |
| 15 | 女性 | してない |
| 16 | 男性 | してない |
| 17 | 男性 | してる |
| 18 | 男性 | してない |
| 19 | 男性 | してない |
| 20 | 女性 | してる |
| 21 | 男性 | してない |
| 22 | 女性 | してない |
| 23 | 女性 | してない |
| 24 | 女性 | してる |
| 25 | 女性 | してない |
| 26 | 男性 | してる |
| 27 | 男性 | してる |
| 28 | 女性 | してる |
| 29 | 男性 | してる |
| 30 | 男性 | してる |
| 31 | 女性 | してない |
| 32 | 女性 | してない |
| 33 | 男性 | してる |
| 34 | 女性 | してる |
| 35 | 男性 | してない |
| 36 | 男性 | してる |
| 37 | 女性 | してない |
| 38 | 女性 | してる |
| 39 | 男性 | してない |
| 40 | 女性 | してる |
| 41 | 男性 | してない |
| 42 | 女性 | してない |
| 43 | 男性 | してる |
| 44 | 男性 | してない |
| 45 | 男性 | してない |
| 46 | 男性 | してる |
| 47 | 女性 | してない |
| 48 | 女性 | してない |
| 49 | 男性 | してない |
| 50 | 男性 | してない |
| 51 | 男性 | してる |
| 52 | 男性 | してる |
| 53 | 男性 | してる |
| 54 | 男性 | してる |
| 55 | 女性 | してない |
| 56 | 男性 | してない |
| 57 | 男性 | してない |
| 58 | 女性 | してる |
| 59 | 女性 | してない |
| 60 | 男性 | してる |
| 61 | 女性 | してない |
| 62 | 男性 | してる |
| 63 | 男性 | してる |
| 64 | 女性 | してない |
| 65 | 女性 | してない |
独立性の検定を行い性別によって副業有無に差があるかを判定します.
帰無仮説は「性別と副業有無は独立している」となり,対立仮説は「性別と副業有無は独立していない」と設定します.
有意水準α=0.05で行います.
Excelを用いたp値の計算手順
Excelを用いたp値の計算手順について説明します.
以下のような観測度数のクロス集計表と期待度数のクロス集計表を作成して,p値を求めます.
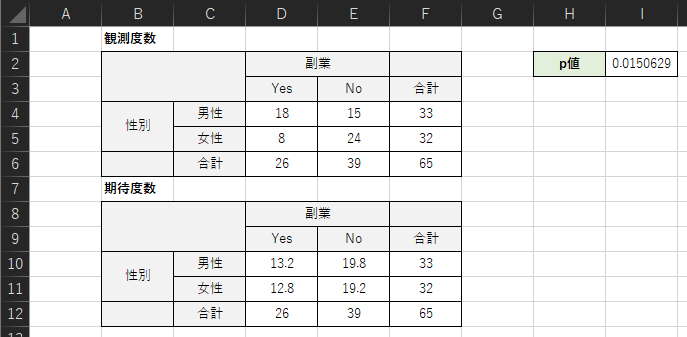
各セルの入力式は以下になります.
・D10:=D6*F4/F6
・E10:=E6*F4/F6
・D11:=D6*F5/F6
・E11:=E6*F5/F6
・I2:=CHISQ.TEST(D4:E5,D10:E11)
計算手順について説明します.
① 観測度数のクロス集計表を作成する【D4-6】【E4-6】【F4-6】
ローデータ(サンプルデータ)からクロス集計表を作成します.Excelを用いたクロス集計表の作成方法についてはこちらのページで解説しています.
② 期待度数を求める【D10-11】【E10-11】
観測度数から各セルの期待度数を求めます.
説明のため観測度数のクロス集計表のセルに,以下のような記号を付します.
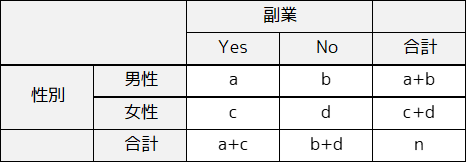
各セルの期待度数は以下の式で求めることができます.

③ p値を求める【I2】
観測度数と期待度数からp値を求めます.ExcelではCHISQ.TEST関数を用いて求めることができます.
CHISQ.TEST関数の引数は以下になります.
CHISQ.TEST(”観測度数のが入力されたセル”,”期待度数が入力されたセル”)
例題では有意水準をα=0.05としてp値は0.0150..だったので,有意水準よりp値は小さいことが分かります.これより,「性別によって副業有無に差がある」といった結論が得られました.
ここまでが,Excelを用いての独立性の検定を行う方法です.例題では2×2クロス集計表について説明しましたが,3×4クロス集計表においても全く同じ手順で独立性の検定を行うことができます.
補足① 効果量(クラメールの連関係数)
仮説検定の結果として重要な統計量として効果量があります.効果量は要因が持つ本来の性質であり,サンプルサイズやデータの単位に依存しない指標となります.
カイ二乗検定の効果量はクラメールの連関係数と呼ばれます.クラメールの連関係数については,以下のページで計算方法まで解説しています.
補足② カイ二乗検定の前提条件
カイ二乗検定を行う際に用いるデータの前提条件について説明します.
① カテゴリーデータ
カイ二乗検定で用いるデータはカテゴリーデータ(名義尺度)である必要があります.カイ二乗検定を行う前に作成するクロス集計表自体も,カテゴリーデータであることが作成する前提条件となります.
② 累積度数
アンケートを行い,割合を用いて集計した結果には用いることができません.クロス集計表でも同様に,ある項目に対して何人いたかといった度数で表現したデータが前提条件です.
③ 対応のない場合
クロス集計表の項目(表側・表頭)に対応のない場合にカイ二乗検定を行います.対応のある場合はマクネマー検定を行います.カイ二乗検定とマクネマー検定との違いについても以下のページで解説しています.
④ 期待度数の最小値が5以上
クロス集計表を作成した際に,各セルの値が5以上であることがカイ二乗検定を行う前提条件です.5未満のセル(正確には期待度数)がある場合は,フィッシャーの正確性検定を使用します.
補足③ Excelを用いた検定統計量の計算手順
Excelを用いた検定統計量Χ2の求め方について紹介します.有意差判定を行なうだけであれば,p値が算出できればよいので検定統計量を求める必要はありません.
検定統計量Χ2は以下のような表を作成して求めます.
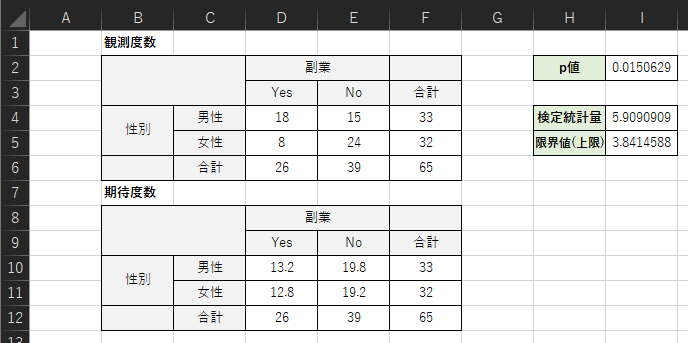
検定統計量Χ2は以下の式で求めることができます.

各セルの対応する観測度数から期待度数引いた値を2乗して,期待度数で割った値の総和となります.Excelでの入力式は以下になります.
I4セルの入力式:=((D4-D10)^2/D10)+((E4-E10)^2/E10)+((D5-D11)^2/D11)+((E5-E11)^2/E11)
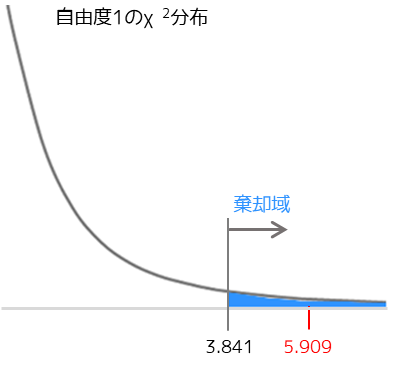
例題では検定統計量Χ2は5.909…となりました.検定統計量を用いて有意差判定を行なう場合は,Χ2分布表から限界値を読み取り大小を比較します.(F分布表の読み方については割愛します)
参考までにExcelではCHISQ.INV.RT関数を用いて,有意水準と自由度から限界値を求めることができます.例題では有意水準α=0.05で,自由度1となるので以下の式で求めることができます.
※ 自由度は表側と表頭の項目数-1を掛けた値です.3×4クロス集計表の場合,(3-1)×(4-1)=6となります.
・限界値(上限):=CHISQ.INV.RT(0.05,1) 【I5】
限界値は3.84…で検定統計量は棄却域にあるため帰無仮説は棄却されます.