StaatAppで一般化線形混合モデルを用いた分析を行う方法を紹介します.SaatAppではCSVファイルやExcelファイルを読み込み,クリック操作だけで一般化線形混合モデルを用いた分析を行うことができます.
StaatAppについては以下をご覧ください.
アプリの基本操作
StaatApp基本操作(データの入出力など)は以下のページで解説しています.
一般化線形混合モデル用ウィンドウの表示
メニューバーから「多変量解析」→「回帰」→「一般化線形混合モデル」を選択して一般化線形混合モデル用ウィンドウを表示します.
ネストされたデータの分析例
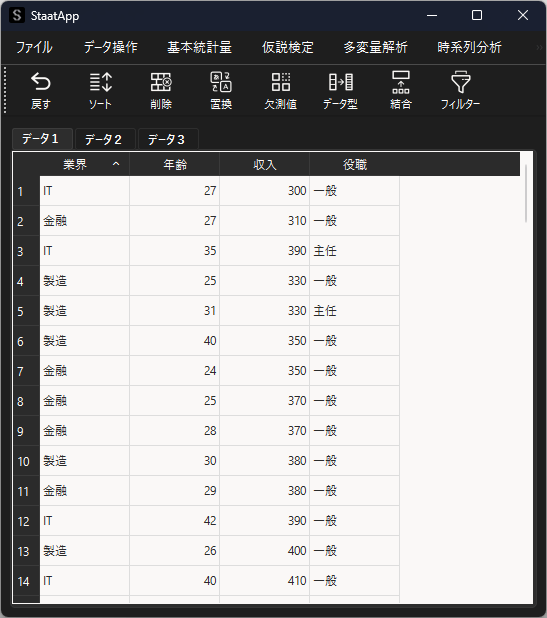
ネストされたデータに対する一般化線形混合モデルを用いた分析例を紹介します.サンプルデータとして,以下のデータを用いて社会人の年齢と年収の関係について分析します.
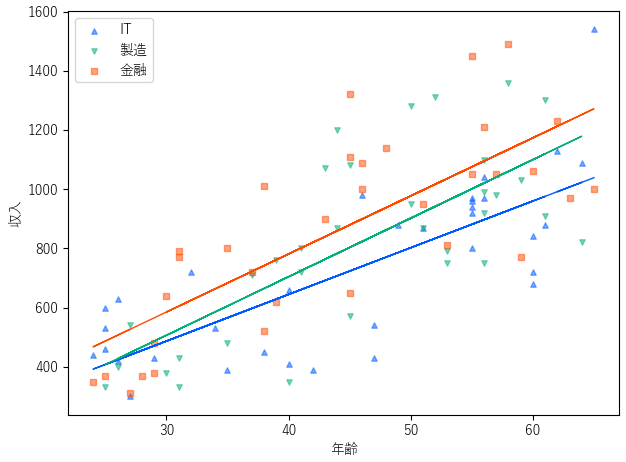
分析を行う前に,散布図機能を用いてデータの分布を確認してみます.業界の違いによって回帰直線の切片や傾きに差があることがわかります.
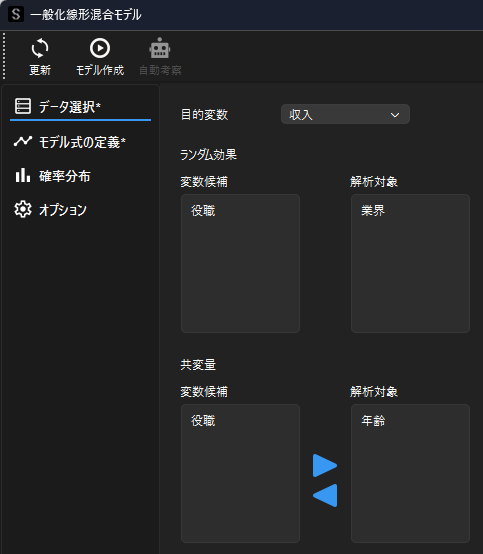
業界の差による影響を考慮して,一般化線形混合モデルを用いた分析を行います.一般化線形混合モデル用のウィンドウを表示したら,データ選択画面で目的変数・ランダム効果・共変量を選択します.
分析例では年収に対する年齢の影響を調べるために,目的変数(従属変数)を”収入”,共変量に”年齢”を設定します.
ランダム効果にはカテゴリーを示す”業界”を選択します.
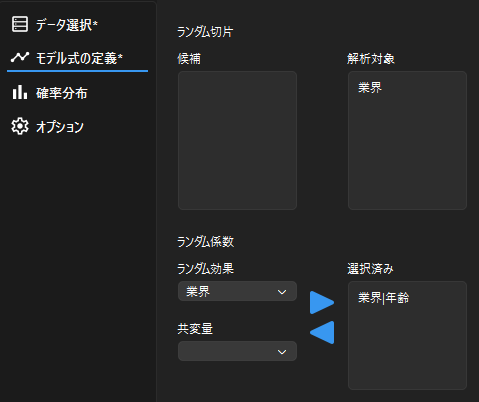
続いてモデル式を定義するために,ランダム切片とランダム係数の設定を行います.
散布図から”業界”によって切片と傾きに差が見られるので,以下のようにランダム切片とランダム係数を設定します.
※ ランダム係数はランダム効果と共変量の組み合わせでモデルを構築します.
「モデル作成」ボタンをクリックすると,画面右側に解析結果が表示されます.
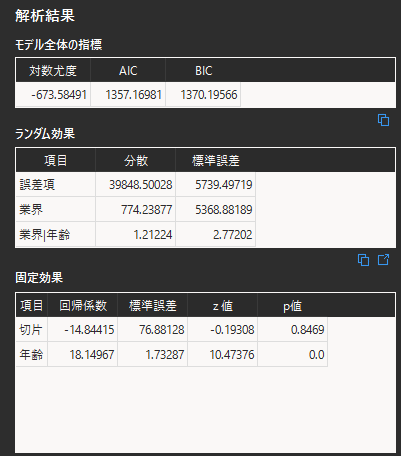
モデルの評価指標では「対数尤度」「AIC(赤池情報量基準)」「BIC(ベイズ情報量基準)」が表示されます.対数尤度は絶対値が小さいほど,AIC・BICは値が小さいほどモデルの当てはまりが良いと言えます.
ランダム効果を見ると誤差項とランダム切片・ランダム係数ごとの分散と標準偏差が表示されます.分散が大きいほどランダム効果の影響の大きいことを示します.例では”業界|年齢”のランダム係数の分散が小さいため,ランダム係数はモデルに対する影響が小さく,不要であったと考えることができます.
固定効果には共変量ごとの統計量が表示されます.回帰係数は目的変数に対する影響の大きさを示し,値が大きいほど目的変数に影響を与えます.共変量が複数ある場合は,共変量間で目的変数への影響度を比較することができます.
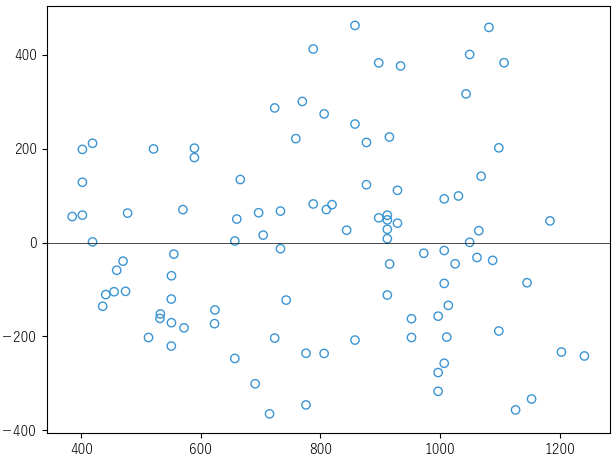
残差プロットは「描画」ボタンをクリックすることで表示することができます.
反復測定データの分析例
反復測定データに対する分析例を紹介します.10人の被験者が繰り返し(3回)受験したテスト結果に,実施時期によって差があるかを調べます.”ID”は個人を示すデータで,同じIDは同一被験者であることを示します.
※ StaatAppの仮説検定では反復測定データ(対応のあるデータ)は,ワイドデータを用いますが,一般化線形混合モデルではロングデータを用います.
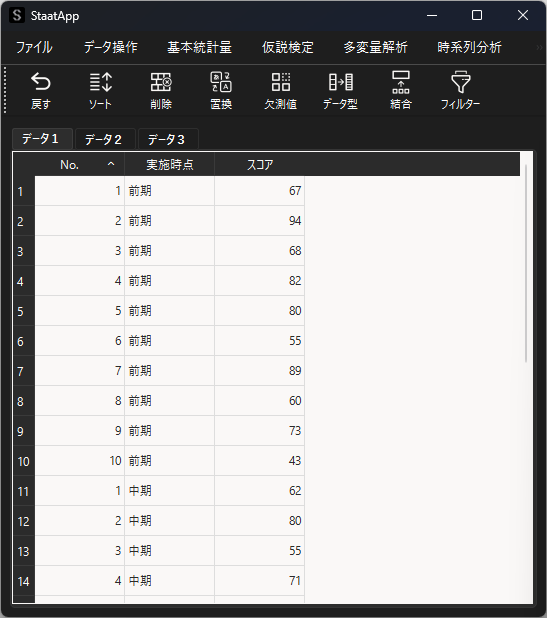
分析を行なう前に,データの前処理としてラベルエンコーディングを行います.一般化線形混合モデルの共変量に設定する値は,数値データのみ使用できるため”実施時点”を数値データに変換します.
置換機能の「ラベルエンコーディング」を用いて変換します.
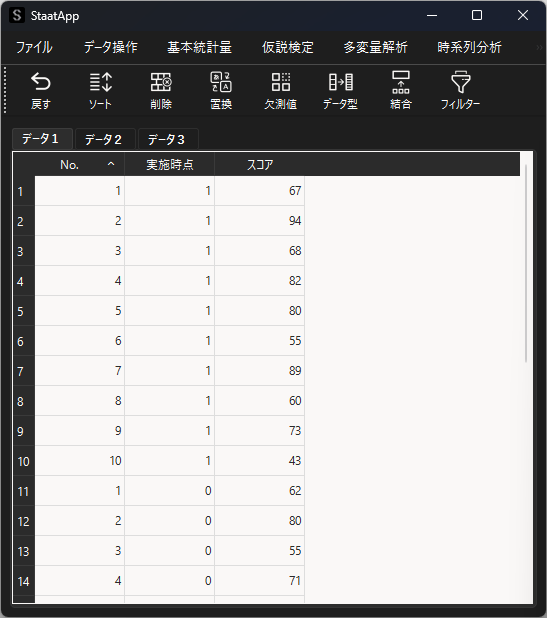
数値データは右寄せ表示されるため,”実施時点”はラベルエンコーディングにより数値データに変換されていることがわかります.
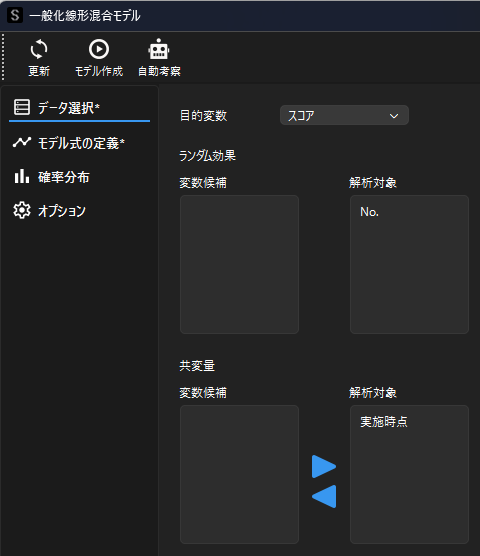
一般化線形混合モデル用ウィンドウで,変数の設定及びモデルの定義を行います.
反復測定データを分析する場合,目的変数に比較するデータ(スコア),ランダム効果に同一個体を示すデータ(No.),共変量に反復測定時点を示すデータ(実施時点)を選択します.
「モデル作成」ボタンを選択して,解析結果を表示します.
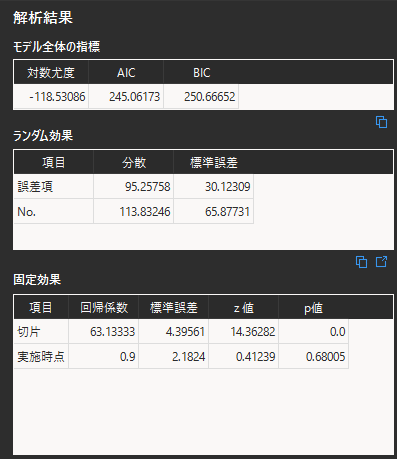
固定効果のp値に検定結果が表示されます.有意水準α=0.05においては,p値>0.05となるため,「実施時点によってテスト結果に差があるとは言えない」という結論が得られます.
反復測定データに対する分析方法は,ランダム効果や共変量に設定する変数によって様々なパターンの仮説検定を行なうことができます.以下の動画解説はEZRを用いた例ですが,StaatAppでも同様の分析が可能なので参考にしてみてください.
確率分布の設定(応用)
一般化線形混合モデルでは,正規分布以外に以下の確率分布が設定可能です.目的変数の性質に合わせて,適切な分布を選択してください.
・プロビット分布
・ロジット分布
・ポアソン分布
・ガンマ分布
自動考察(プレミアムプラン限定)
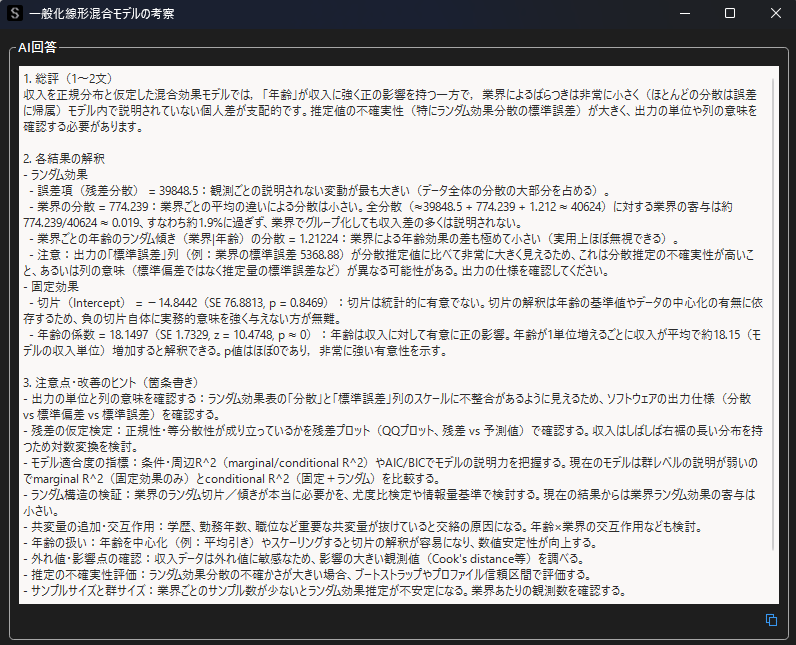
一般化線形混合モデルの解析結果について自動考察を行なうと,ランダム効果と固定効果について,以下のような考察結果を得ることができます.分析例はネストされたデータの解析結果を用いています.
補足① 統計アプリStaatAppとは
StaatAppは計算仮定が複雑な解析手法を,誰でも手軽に素早く行なうことができるアプリです.StaatAppの詳細は以下のページをお読みください.
補足② 一般化線形混合モデルとは
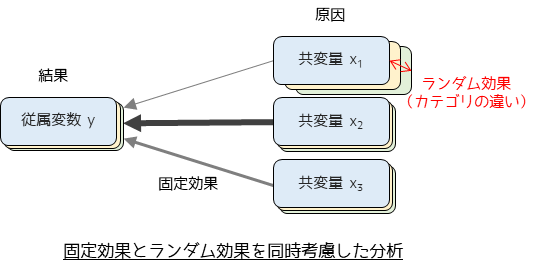
一般化線形混合モデル(Generalized Linear Mixed Models; GLMM)は,統計モデルの一つで,固定効果とランダム効果の両方を考慮します.固定効果はすべての個体やグループに共通する効果を示し,ランダム効果は個体やグループ間のランダムな変動を捉えます.様々なデータに合わせて柔軟なモデルを作成できるため使用場面は多岐にわたりますが,特に繰り返し測定データや階層的なデータ構造を持つデータの分析に適しています.
詳細は以下のページで解説しています.
補足③ アプリの仕様について
アプリではPythonのGPBoostライブラリを用いて一般化線形混合モデルの分析を行っています.
以下の公式ドキュメントに詳細な仕様が記載されています.









