主成分分析(principal component analysis)の具体的な計算方法について,Pythonのsklearnライブラリを用いて解説します.
補足事項として結果の見方や扱うデータの前提条件,プログラムを実行するための準備方法についても解説しています.
Excelファイルから行う主成分分析実行アプリについてはこちら.
主成分分析の手順
主成分分析は以下の手順で行います.
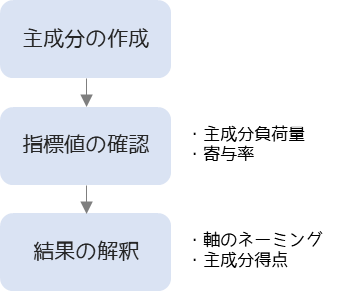
主成分はデータの分散が最大になる方向を示すように作成します.主成分は元データの変数分だけ作成することができ,主成分の分散が大きいものから順に第1主成分,第2主成分,…と言います.
分析結果として作成した主成分・観測変数ごとの主成分負荷量・寄与率を確認します.累積寄与率が80%以上を目安に主成分を選択します.
選択した主成分がどのような意味を持つのか,主成分負荷量から考えます(軸のネーミング).選択した主成分を軸として主成分得点プロットした散布図から,データの特徴を解釈します.
例題の設定
主成分分析を用いた統計解析を説明するために,以下の例題・データを用います.
「社会人21人に対して,副業の有無・収入・性別・年齢・結婚有無についてのデータを収集しました.収集したデータに対して主成分分析を用いて,情報を要約した変数を作成します.」
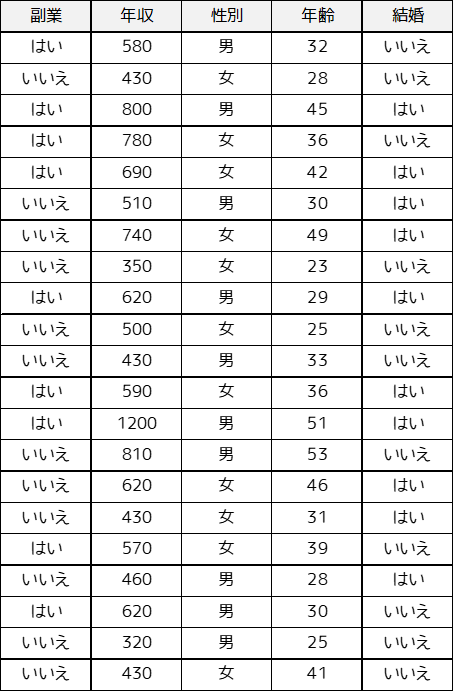
「はい・男」→1,「いいえ・女」→0としてダミー変数に変換して計算は行います.
Pythonで読み込むせるデータ形式(CSVファイル)の作り方はこちら.
プログラムの作成
Pythonを用いてプログラムの作成をします.
主成分分析に必要な記述例は以下になります.(結果の出力方法については次の章で解説しています.)
# ライブラリのインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
# データの読み込み
df_workers = pd.read_csv("sample.csv")
# 変数の標準化
df_workers_std = df_workers.apply(lambda x: (x-x.mean())/x.std(), axis=0)
# 主成分分析の実行
pca = PCA()
pca.fit(df_workers_std)
# データを主成分に変換
pca_row = pca.transform(df_workers_std)それぞれの記述内容について解説します.
① ライブラリのインポート
主成分分析で用いるライブラリをインポートします.
4つのライブラリをインポートしますが,記述例と全く同じ内容で問題ありません.
# ライブラリのインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA② データの読み込み
pd.read_csv関数を用いてCSVファイルの読み込み,データフレームに格納します.
データフレーム名(=の左側)は任意の値を入力します.””内は読み込むCSVファイル名を記述します.
# データの読み込み
df_workers = pd.read_csv("sample.csv")③ 変数の標準化
sklearnでは分散共分散行列を用いて主成分を行うため,各項目の分散による影響を無くすため変数の標準化を行います.
”データフレーム名”.apply(lambda x: (x-x.mean())/x.std(), axis=0)
という式で標準化が行えます.
# 変数の標準化
df_workers_std = df_workers.apply(lambda x: (x-x.mean())/x.std(), axis=0)④ 主成分分析の実行
sklearnライブラリのPCA関数を用いて,主成分分析を行います.
主成分に変換では,”pca_row”というデータフレームの列ごとに主成分を格納しています.(1列目は第1主成分,2列目は第2主成分,,,となります)
# 主成分分析の実行
pca = PCA()
pca.fit(df_workers_std)
# データを主成分に変換
pca_row = pca.transform(df_workers_std)PyCharmを用いている方は右上の「▶」ボタンを押すとプログラムが実行されます.(ここまでの手順だけでは結果は出力されないので注意してください)
結果の出力・解釈
主成分分析の結果を3つの方法で出力・解釈します.
① 各主成分への寄与率と累積寄与率を求める
主成分分析で合成した各主成分に対して,寄与率と累積寄与率を求めます.寄与率とは,各主成分がどれだけの情報を説明できているかという指標になります.
# 寄与率を求める
pca_col = ["PC{}".format(x + 1) for x in range(len(df_workers_std.columns))]
df_con_ratio = pd.DataFrame([pca.explained_variance_ratio_], columns = pca_col)
print(df_con_ratio.head())
# 累積寄与率を図示する
cum_con_ratio = np.hstack([0, pca.explained_variance_ratio_]).cumsum()
plt.plot(cum_con_ratio, 'D-')
plt.xticks(range(5))
plt.yticks(np.arange(0,1.05,0.05))
plt.grid()
plt.show()寄与率を求めるための記述は少し複雑ですので説明は省略します.2行目の”df_workers_std”の部分だけ変数の標準化で指定したデータフレーム名に置き換えて記述すれば求めることができます.
累積寄与率についても,nampyライブラリを用いているため説明は省略します.寄与率を求める際に,データフレーム名(2行目の”df_workers_std”部分)以外変えていない方は全てコピペで問題ありません.
出力結果は以下になります.
PC1 PC2 PC3 PC4 PC5
0 0.449831 0.211547 0.169386 0.1427 0.026535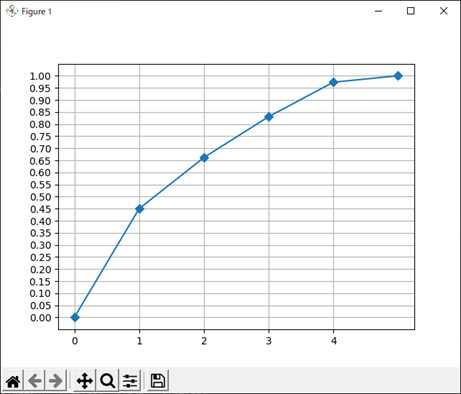
第1主成分の寄与率は,0.449..であることが分かります.また,累積寄与率は表現したグラフから第3主成分までで約83%の情報を説明できているということが分かります.
一般的には,累積寄与率が80%以上になる主成分数を採用して分析結果に用いることが多いです.
② 主成分負荷量を求める
主成分負荷量とは,各主成分に対する各変数の影響度合いになります.-1から1の間の値を取り,絶対値が大きいほど影響度が大きくなります.主成分負荷量を求めることで,各主成分が何を意味しているかが分かりやすくなります.
# 主成分負荷量を求める
df_pca = pd.DataFrame(pca_row, columns = pca_col)
df_pca_vec = pd.DataFrame(pca.components_, columns=df_workers.columns,
index=["PC{}".format(x + 1) for x in range(len(df_pca.columns))])
print(df_pca_vec)
# 主成分負荷量を図示する
plt.figure(figsize=(6, 6))
for x, y, name in zip(pca.components_[0], pca.components_[1], df_workers.columns[0:]):
plt.text(x, y, name)
plt.scatter(pca.components_[0], pca.components_[1])
plt.grid()
plt.xlabel("PC1")
plt.ylabel("PC2")
plt.show()主成分負荷量を求める際も,複雑なデータフレーム操作が必要になります.基本的にはデータフレーム名(df_workers)を置き換えるだけでコピペ可能なのでそのまま使うことができます.
第1主成分と第2主成分の主成分負荷量をプロットした散布図は,ここまでに計算した変数を用いて作成することができます.9行目の”df_workers”の部分だけは,定義したデータフレーム名に置き換えてください.
出力結果は以下になります.
side_job income sex age married
PC1 0.411365 0.628269 0.148789 0.533280 0.359905
PC2 -0.353195 -0.017265 -0.828095 0.345272 0.264580
PC3 0.547065 0.128213 -0.449148 0.020872 -0.694343
PC4 -0.556708 0.185039 0.268997 0.516309 -0.562941
PC5 -0.311174 0.744515 -0.134269 -0.573924 -0.038092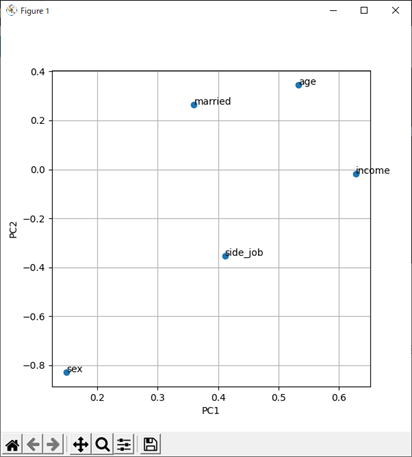
第1主成分に対して主成分負荷量が大きい項目は,年収と年齢であることがわかります.つまり,第1主成分は”社会的地位”を表す指標とも捉えることができます.
第2主成分に対して主成分負荷量が大きい項目は,性別と副業の有無になります.2つの変数とも負の値であることから,正方向に対しては”Netflixをよく見る女性(副業をしていない女性)”を表す指標と捉えることができます.
③ 主成分得点を求める
主成分得点とは,各主成分を軸とした場合のサンプル(回答者)の点数になります.一般的には散布図を用いて分析が行われ,プロットされたデータの位置関係から各サンプルの特徴を見ることができます.
主成分分析で合成した第1主成分と第2主成分の2軸で散布図を作成します.
# 主成分得点を求める
plt.figure(figsize=(6, 6))
plt.scatter(pca_row[:, 0], pca_row[:, 1], alpha=0.8)
plt.grid()
plt.xlabel("PC1")
plt.ylabel("PC2")
x = pca_row[:, 0]
y = pca_row[:, 1]
annotations = df_workers_std.index
for i, label in enumerate(annotations):
plt.annotate(label, (x[i], y[i]))
plt.show()散布図の作成はmatplotライブラリのpyplotモジュールを用いて行います.
3行目のscatterメソッドで散布図の描画設定を行います.引数の形式はplt.scatter(x, y, c=”色”, alpha=”透明度”になります)
【matplotlib.pyplot.scatterメソッドの引数について】
・x:散布図の描画するデータのx座標を指定します.x座標は主成分に変換したデータフレーム”pca_row”の1列目を設定します.
・y:散布図の描画するデータのy座標を指定します.y座標は主成分に変換したデータフレーム”pca_row”の2列目を設定します.
・alpha:0~1の間でプロットされるデータの透明度を指定します.
その他の行はそのままの記述で問題ありません.
出力結果は以下のように解釈することができます.
※ 第1主成分(PC1)は”社会的地位”,第2主成分は”Netflixをよく見る女性”を示す指標です.
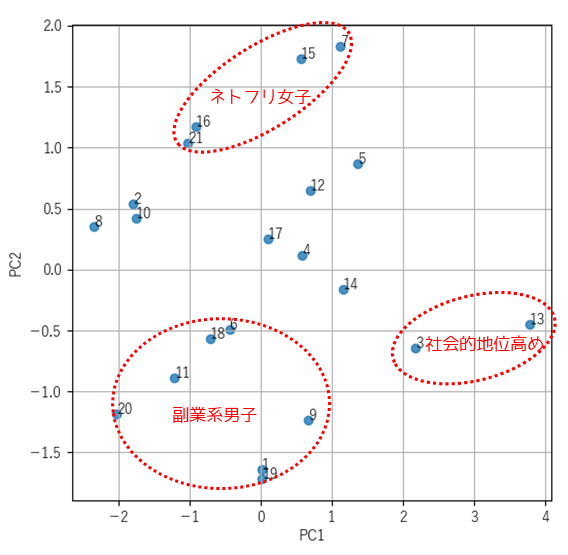
散布図の左下に位置する回答者は,副業を行っている男性かつ社会的地位がそれほど高くないと捉えることができます.
ここまでが,主成分分析の結果の出力方法と解釈になります.
補足① 主成分分析とは
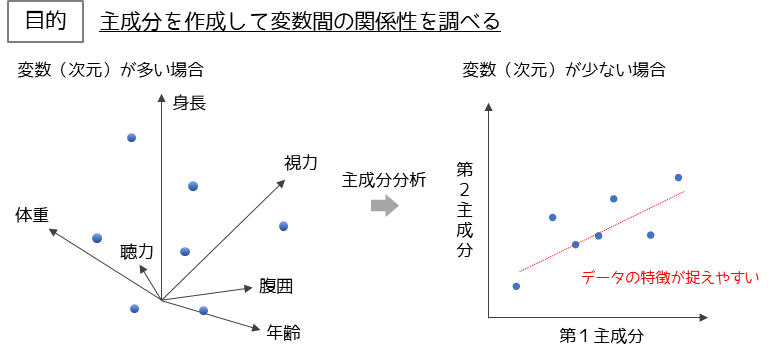
主成分分析とは多数の変数に含まれている情報を要約して,少数の変数で表す多変量解析の1つです.
変数が多い場合データの特徴が直感的に分かりづらいですが,変数(次元)を少なくすることでデータの特徴が捉えやすくなります.2つの主成分に要約した場合は,平面の散布図としてデータを見ることができます.
補足② 因子分析との違い
因子分析は主成分分析と類似した分析手法ですが,考え方や目的は大きく異なります.
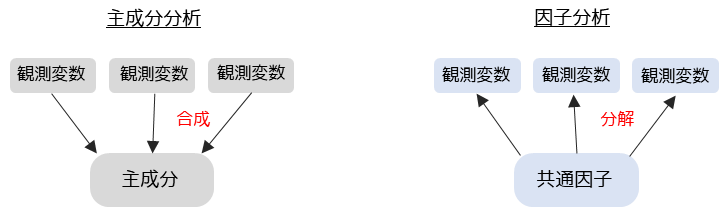
因子分析は多変量解析の中でも,観測変数に影響を与えている共通因子を抽出するために用います.観測変数を要約する主成分分析とは,正反対の分析方法になります.
補足③ 主成分分析を行う前提条件
主成分分析は,多変量解析の中でも扱うデータの前提条件が非常に少ない分析手法です.しかし,以下の2つの条件については注意してください.
① 量的変数
主成分分析の対象データは量的変数である必要があります.アンケートの調査結果などで質的変数を含んでいるデータを扱う場合は,ダミー変数を用いる必要があります.
② 変数間(項目間)に逆相関がない
変数間に逆相関があるデータは,主成分分析を行うことができません.
変数間に逆相関がある場合,特定の項目の値が高いほど逆相関がある項目の値が低くなります.この場合,主成分分析で求めた各主成分は”総合力”といった意味を持たなくなります.
補足④ 統計解析アプリ
本サイトではより手軽に主成分分析を実行して,主成分得点・寄与率・主成分負荷量の算出・グラフ作成を行うアプリ(StaatApp)を販売しています.
詳細は以下のページで紹介しています.
》StaatAppで行う主成分分析
》統計解析アプリStaatAppとは
補足⑤ PyCharmを用いた実行環境の構築
Pythonを初めて使う方や,自分のPCにPython・PyCharmが入っていない方は以下のページで解説している手順で実行環境の構築を行ってください.
初めて触る方にもわかりやすいようにPyCharmを用いた手順となっています.
主成分分析では,”sklearn”というライブラリを使用します.インストール方法が分からない方は,ライブラリのインストールを参考にしてください.
》実行環境の構築方法【Pycharm使用】
》ライブラリのインストール方法【Pycharm使用】
補足⑥ Pythonで読み込むデータの作成方法
Pythonで扱うCSVファイルの作成方法は以下のページで解説しています.