StaatAppでメタアナリシスを実行する方法を紹介します.SaatAppではCSVファイルやExcelファイルを読み込み,クリック操作だけでフォレストプロットやファンネルプロットを作成することができます.
アプリの基本操作
StaatApp基本操作(データの入出力など)は以下のページで解説しています.
カテゴリーデータに対するメタアナリシス
カテゴリーデータつまり,オッズ比やリスク比を用いたメタアナリシスの実行方法を説明します.
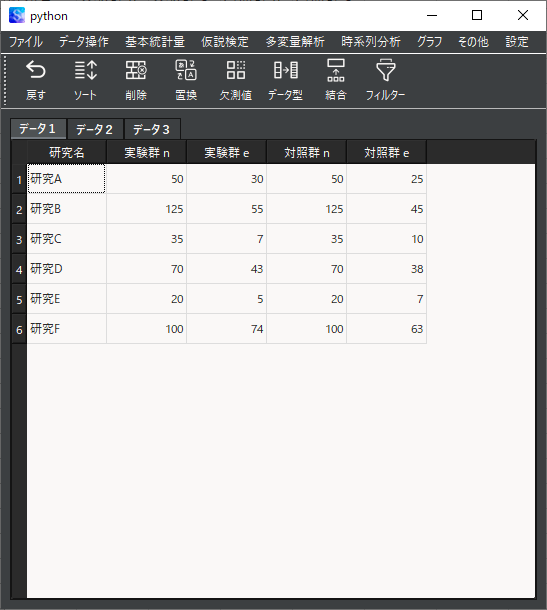
分析用のデータとして,以下のように研究名と比較する2群(実験群・対照群)ごとのサンプルサイズ,イベント発生数を用意します.
メニューバーから「その他」→「メタアナリシス」→「比率のメタアナリシス」を選択します.
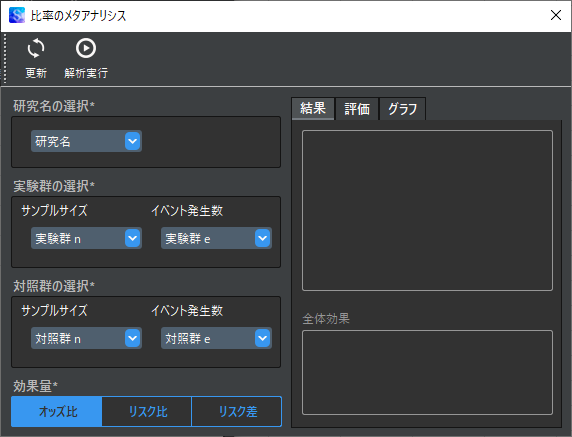
比率のメタアナリシス用ウィンドウが表示されたら,各項目に分析対象の変数を選択します.
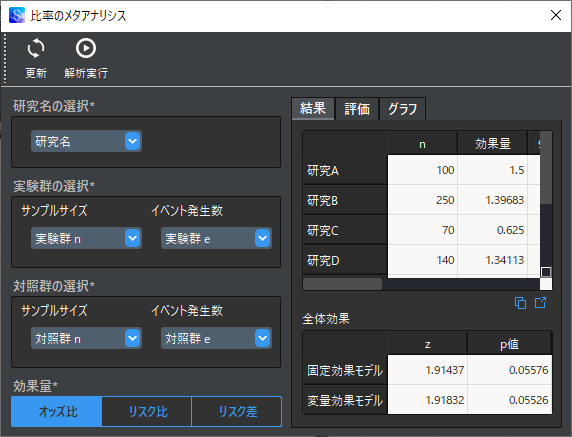
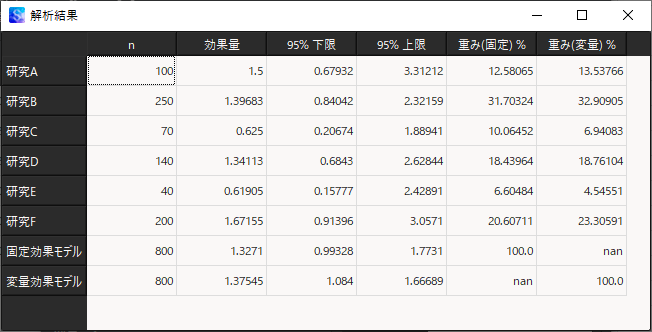
「解析実行」ボタンをクリックすると,メタアナリシスの結果が画面右側に表示されます.選択した効果量と,固定効果モデル・変量効果モデルによる統合効果,重みなどが表示されます.
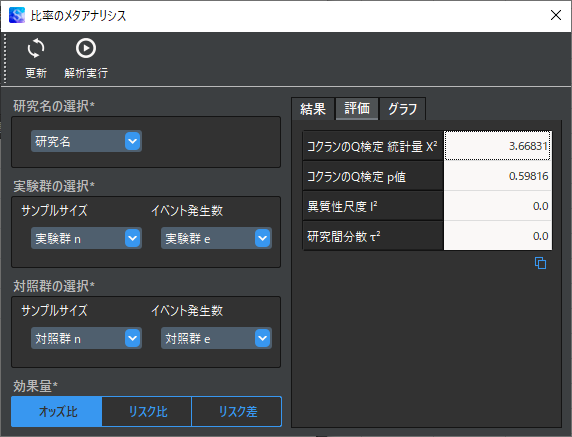
「評価」タブを選択すると,コクランのQ検定の結果や異質性尺度 I² の結果が表示されます.
「グラフ」タブでは,フォレストプロットとファンネルプロットを作成することができます.
フォレストプロットではモデルを選択して,「作成」ボタンをクリックすると以下のようなフォレストプロットが表示されます.
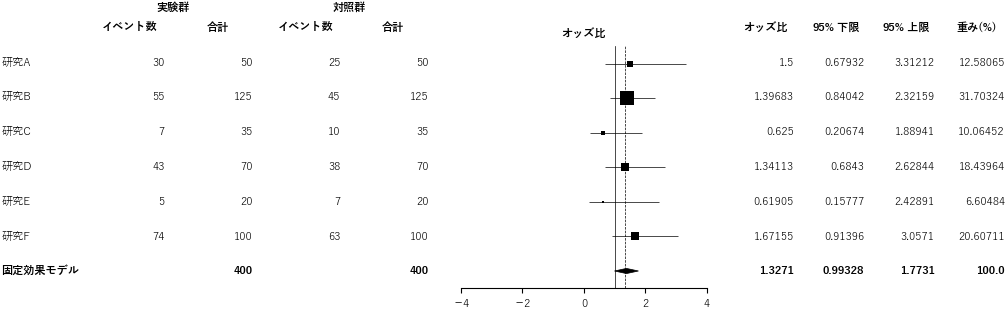
フォレストプロットのプロットエリアの設定などは「詳細設定」から,自由に変更することができます.
ファンネルプロットの「作成」ボタンをクリックすると,以下のようなファンネルプロットが表示されます.
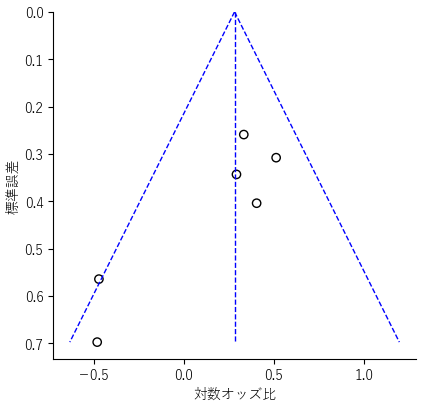
リスク比・リスク差についても効果量の設定を変更することで,同様の解析を行うことが可能です.
連続データに対するメタアナリシス
連続データつまり,平均差や標準化平均差を用いたメタアナリシスの実行方法を説明します.
分析用のデータとして,以下のように研究名と比較する2群ごとのサンプルサイズ,平均値,標準誤差を用意します.
※ 標準誤差は文献に記載されている,信頼区間から算出することができます.
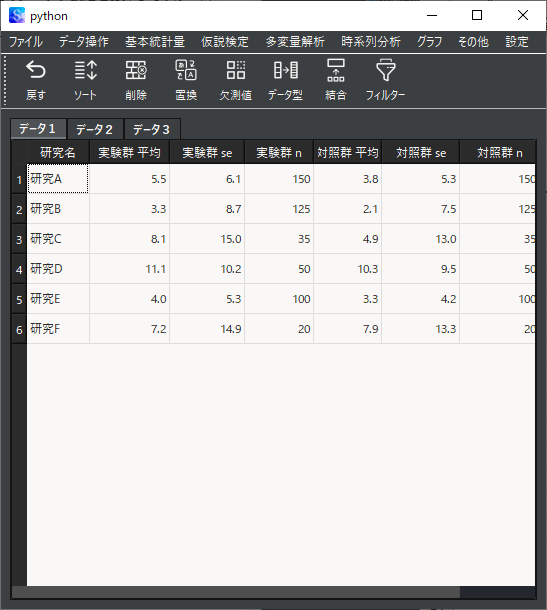
メニューバーから「その他」→「メタアナリシス」→「平均値のメタアナリシス」を選択して,分析用ウィンドウを表示します.
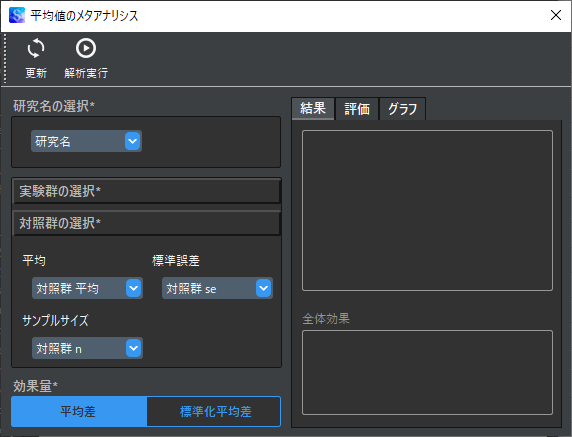
上記のように分析対象の変数を選択して,「解析実行」ボタンをクリックすると計算結果が表示されます.
計算結果の表示内容と,グラフの作成方法は比率のメタアナリシスと同様になります.フォレストプロットについては,表示項目が比率のメタアナリシスとは異なり,以下のようになります.
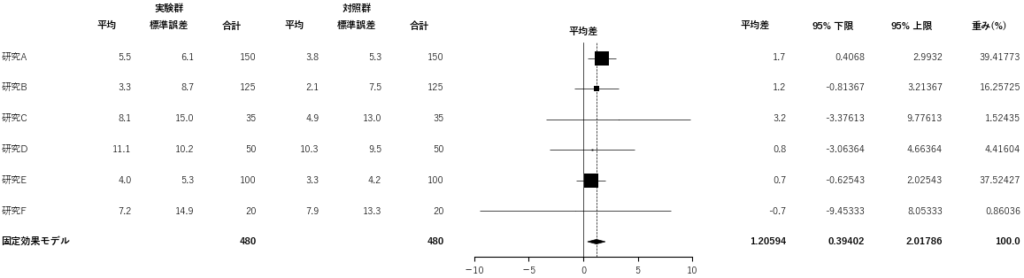
標準化平均差についても効果量の設定を変更するだけで,同様の解析を行うことが可能です.
一般化逆分散法によるメタアナリシス
一般化逆分散法を用いたメタアナリシスでは,ここまで紹介したカテゴリーデータと連続データの両方のデータを扱うことができます.
分析画面は以下のようになっており,研究ごとに効果量,標準誤差,2群ごとのサンプルサイズが必要になります.
※ 標準誤差は文献に記載されている,信頼区間から算出することができます.
例としてリスク比を用いたメタアナリシスを行いたい場合は,効果量として各研究のリスク比をデータとして用意して,以下のように変数と効果量を選択します.
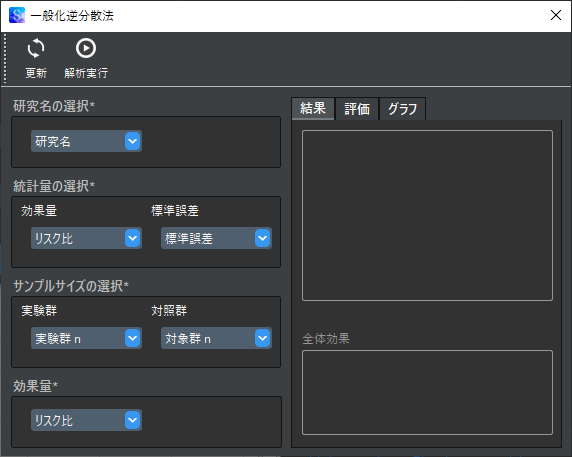
一般化逆分散法では,群ごとのイベント発生数や平均値,標準誤差が必要ないので,文献から得られるデータに制限や不整合がある場合に,役立つことが多いです.
一般化逆分散法では,オッズ比,リスク比,リスク差,平均差,標準化平均差を効果量として扱うことができます.
補足① 統計アプリStaatAppとは
StaatAppは計算仮定が複雑な解析手法を,誰でも手軽に素早く行なうことができるアプリです.StaatAppの詳細は以下のページをお読みください.
補足② メタアナリシスについて
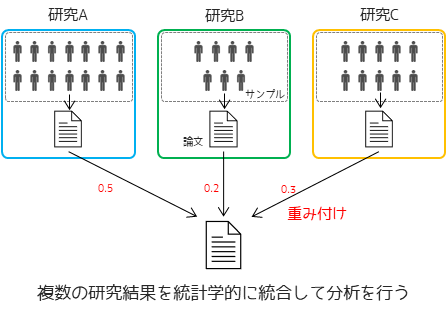
メタアナリシスとは,複数の研究結果(学術論文)を統計学的に統合して,分析を行う手法です.特に医学分野の研究でよく用いられる手法で,例えば飲酒習慣とがん発症の関連性に関する既存研究が複数あった場合に,それらの研究結果を統合して新たに関連性を判断したりします.
メタアナリシスについての詳細や分析手順,結果の読み方などは以下のページで解説しています.
補足③ 統合効果モデル
メタアナリシスでは統合効果を算出する方法・モデルとして,様々な手法が存在します.StaatAppではRなどで最も用いれているモデルを採用しています.
具体的には,効果量・モデル種別ごとに以下の手法を採用しています.
| オッズ比/リスク比/リスク差 | 平均差/標準化平均差/ハザード比 | |
| 固定効果モデル | Mantel-Haenszel法 | 一般化逆分散法 |
| 変量効果モデル | DerSimonian-Laird法 | DerSimonian-Laird法 |









