機械学習でよく用いられる決定木について,実践例を用いて解説します.
実践例で使用している統計解析アプリStaatAppはこちらのページから無料でダウンロードできます.
決定木とは
ある条件に基づきデータを2分割して,さらにその結果に基づきデータを分割するという作業を繰り返すアルゴリズムです.
具体的に,決定木を用いて社会人集団のデータから副業の有無を分類する例を考えてみます.(判定内容等は全て仮定です)
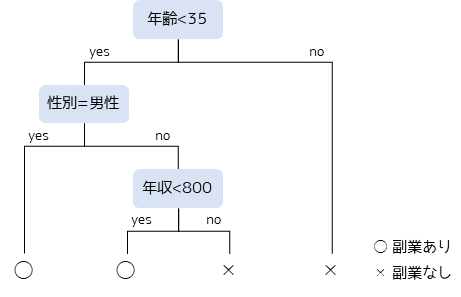
まず,各社会人の”年齢”という数値から副業有無の可能性を分類します.年齢が若いほど,特に35歳未満であれば副業を行っている可能性が高い場合,図のようなしきい値で判定が行われます.
次に年齢が35歳未満で性別が”男性”であった場合,最終的に”副業あり”と判定します.また,年齢が35歳以上もしくは,35歳未満かつ女性かつ年収が800万以上の人は”副業なし”と判定します.
このように決定木では特徴量(属性や数値)をもとに分岐を繰り返して,データの分類・予測を行います.分岐条件を可視化した際の図を反対にすると”木”のように見えることから,決定木と呼ばれています.
決定木分析の手順
決定木を用いた分析・予測は基本的には以下の手順で行います.
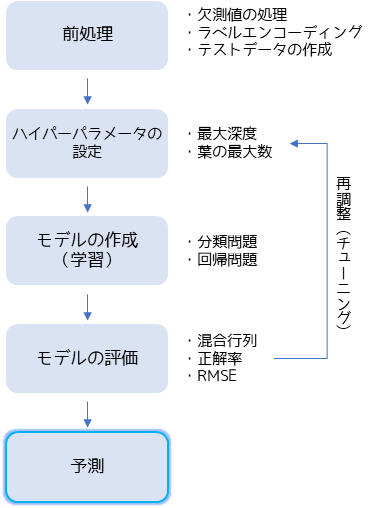
決定木分析でははじめにデータの前処理を行います.欠測値がある場合は補完や補正を行い,カテゴリーデータがある場合は置換などでエンコーディングを行います.テストデータは学習したモデルを評価するために作成します.機械学習ではデータを分割することで作成することが多いです.
分析者が設定できるモデルのパラメータ(設定値)をハイパーパラメータと言い,実際に機械学習を行うためにパラメータの設定を行います.(StaatAppでははじめはデフォルト設定で問題ありません.)
モデルの作成(学習)では主に分類問題と回帰問題の2パターンがあります.分類問題はターゲット変数(決定木で予測したい変数)がカテゴリーデータの場合に行い,回帰問題はターゲット変数が数値データの場合に行います.
モデルを作成したらテストデータを用いてモデルの評価を行います.分類問題では混合行列を作成して,正解率や再現率で評価します.回帰問題ではRMSE(二乗平均平方根誤差)やR²(決定係数)でモデルの精度を評価します.
再度ハイパーパラメータの調整(パラメータチューニング)を行い精度が十分と判断した場合,作成したモデルを用いてターゲット変数の予測を行います.
StaatAppを用いた決定木
統計解析アプリStaatAppを用いて,実際に決定木を用いた学習・予測を行います.データサイエンス・機械学習の競技プラットフォームであるKaggleで使用されるタイタニック号のデータセットを用いて解説します.
予測対象は生存状況の有無として,決定木を用いた分類問題を行います.
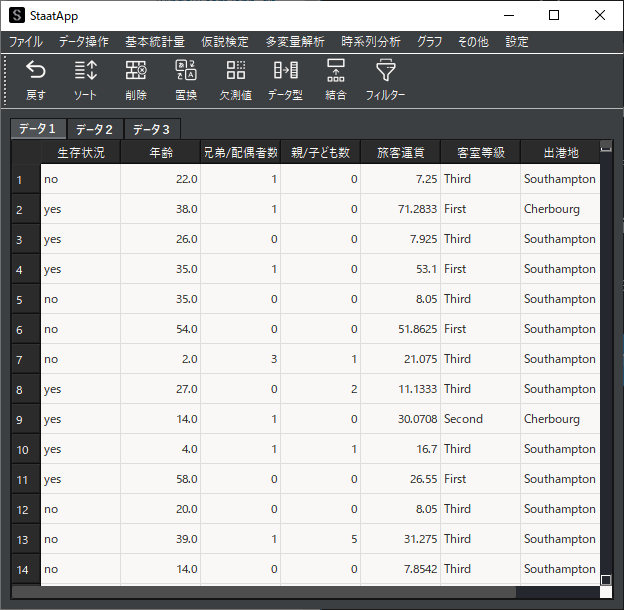
① 前処理
欠測値の処理やラベルエンコーディング(置換)の方法は以下のページをお読みください.
ここではテストデータの作成を行います.データ操作画面(初期画面)のメニューバーの「データ操作」からテストデータ作成機能を用いて,学習データとテストデータに分割します.
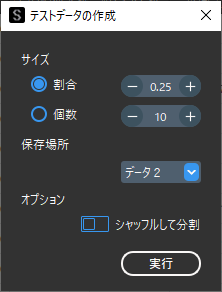
デフォルト設定のまま「実行」を行うと,全データの下から25%のデータがテストデータとして分割され「データ2」に保存されます.ホールド・アウト検証を行う場合に適しています.
ランダムでデータを分割したい場合は,「シャッフルして分割」をオンにします.
② ターゲット変数・特徴量の選択
決定木機能を選択して決定木用のウィンドウを表示します.
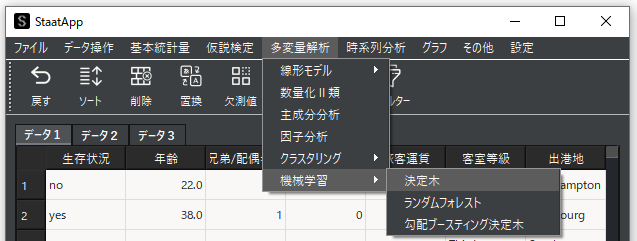
ターゲット変数(目的変数)には分類を行いたい変数を,特徴量(説明変数)には分類するための基準とする変数を選択します.
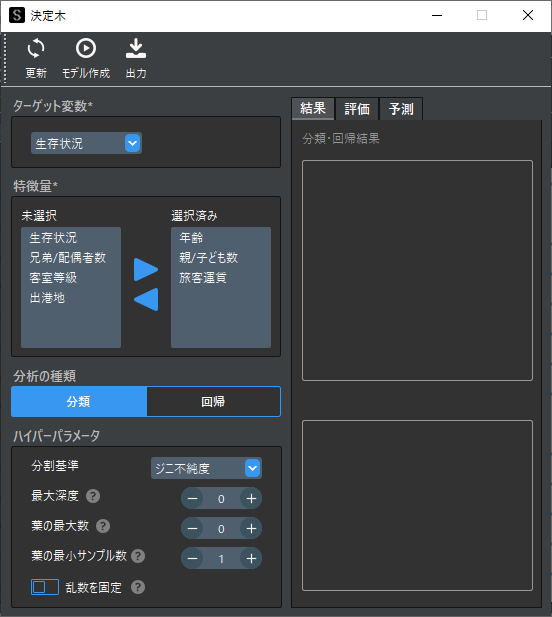
③ ハイパーパラメータの設定
ハイパーパラメータを調整することで過学習や未学習を避け,モデルの予測精度を向上させることができます.各設定項目については補足①をお読みください.
例ではデフォルト設定に加えて最大深度を”3″に設定します.
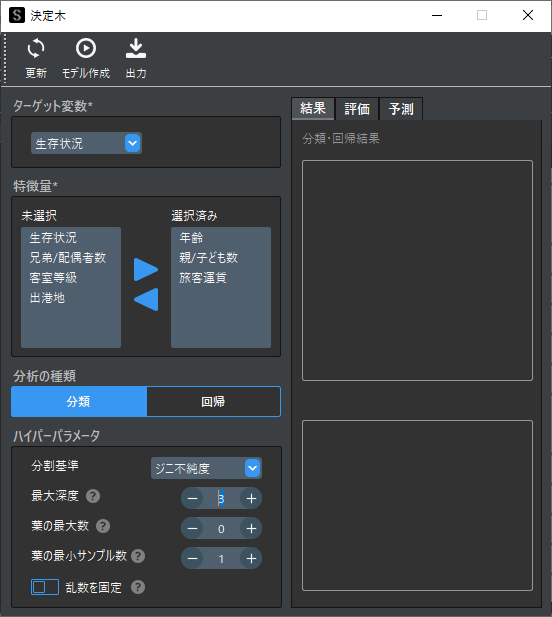
④ 学習の実行
ツールバーの「モデル作成」ボタンでモデルの作成を実行します.
分類問題では以下のように,木構造のグラフが作成されます.
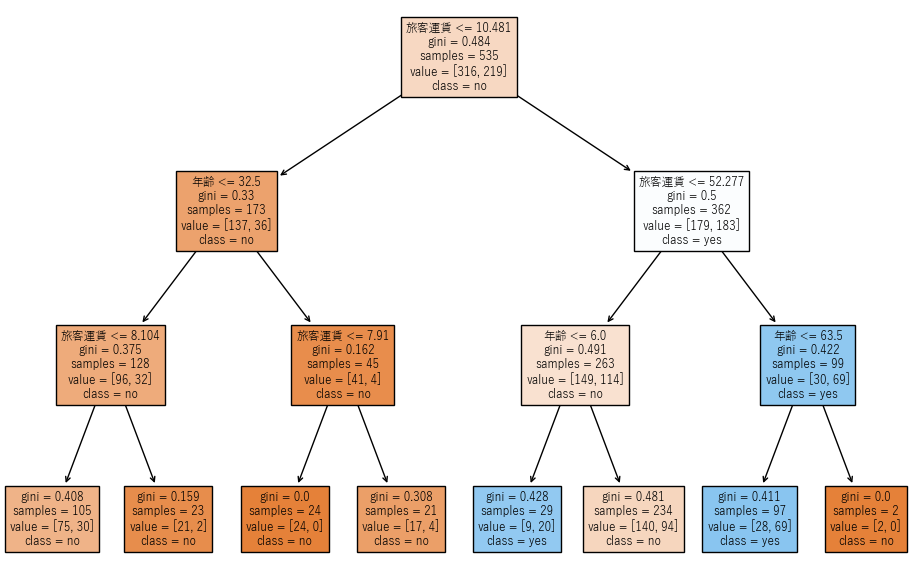
木構造の見方としては一番上の枠(ノード)の1行目に書かれている特徴量が,最も分類結果に影響を与えている特徴量になります.例では生存有無に最も影響を与えているのは旅客運賃となります.
3行目の「samples」このノードでのサンプル数を示し,4行目の「value」は現段階での構成比(生存有無のno=316, yes=219)を示します.
1つ目の条件が”True”であった場合に左のノードに進み,”False”であった場合に右のノードに進みます.例では旅客運賃が10.484ポンド以下であった場合に,左のノードに進みます.
ノードの色は構成比の偏りを示し,生存有無でnoが多いほどオレンジ色,yesが多いほど青色になります.
画面右側の解析結果にはサンプルごとの分類結果と特徴量ごとの重要度(影響度)が表示されます.
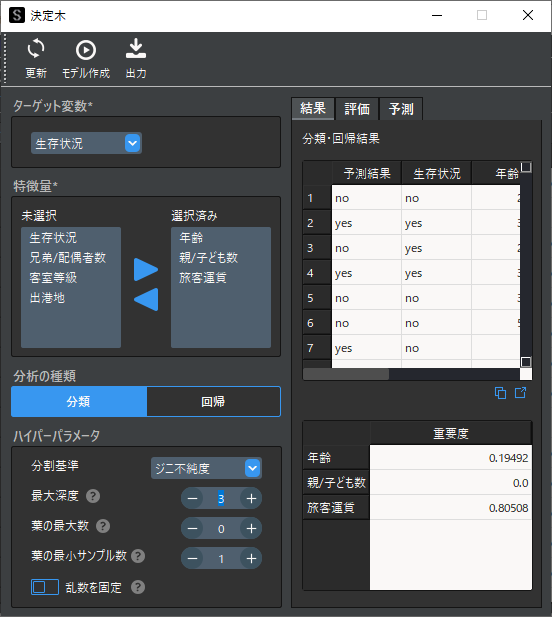
重要度からも旅客運賃が最も分類結果に影響を与えていることがわかります.
⑤ モデルの精度評価
作成したモデルに対して,テストデータを用いてモデルの精度評価を行います.
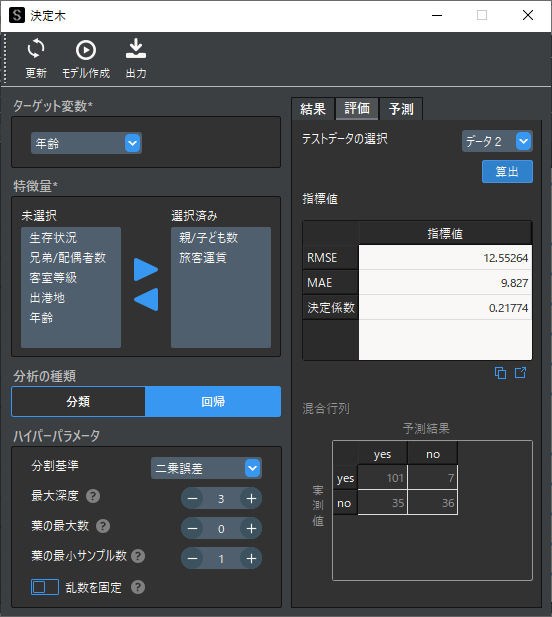
評価タブを表示してテストデータに「データ2」を選択します.「算出」ボタンをクリックすると以下のようにに4つの評価指標と混合行列が表示されます.
評価指標はそれぞれ値が大きいほどモデルの予測精度が高いことを意味します.混合行列はテストデータ(実測値)と予測値を比較した行列で,生存有無が”yes”の場合はほとんど予測が的中していることがわかります.
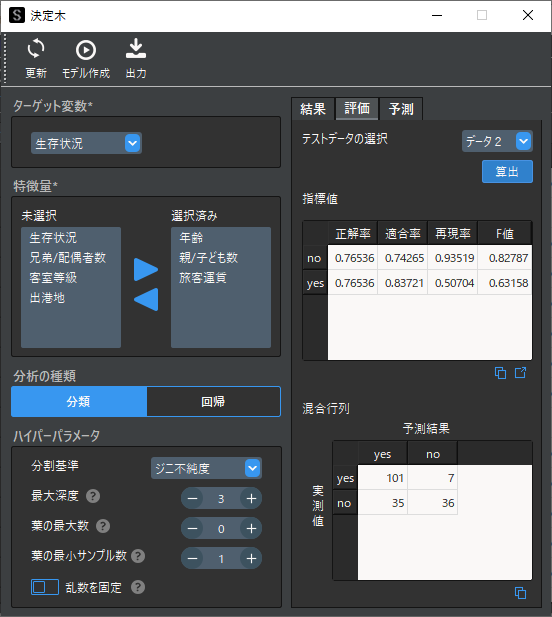
予測精度が十分でない場合は,ハイパーパラメータを調整して再度学習を実行します.
⑥ 予測値の算出
作成したモデルに対して予測用データを読み込ませて,ターゲット変数の予測を行います.
予測タブを表示し予測用データの選択,「算出」ボタンをクリックすると予測結果が表示されます.
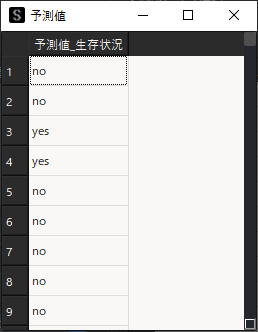
ここまでがStaatAppを用いた基本的な決定木分析の手順になります.
補足① ハイパーパラメータ
決定木分析におけるハイパーパラメータの説明とチューニング方法は以下になります.
| 種別 | 説明・チューニング方法 |
| 分割基準 | 分類問題では”ジニ係数”・”エントロピー”・”シャノンゲイン情報”から選択します.ジニ係数の方が連続データに強く,カテゴリーデータに対してはエントロピーが強いとされています. 回帰問題では”二乗誤差”・”平均二乗誤差”・”絶対誤差”・”ポアソン逸脱度”から選択可能です. |
| 最大深度 | ツリーの最大深度は値が大きいほど,深く分割を行います.デフォルト設定では全ての葉が1になるまで分割されます. 過学習を防ぐためには最大値を設定します.また,過学習の防止に最も効果がある場合が多いです. |
| 葉の最大数 | 最大の葉の数が多いほど分割されます.デフォルト設定では葉の数は無制限です. 過学習を防ぐためには値を小さくして,分割回数を制限します. |
| 葉の最小サンプル数 | 葉を構成するのに必要な最小限のサンプルの数になります. 値が小さいと過学習になる可能性があります. |
| 乱数の固定 | 学習ごとに用いられる乱数を固定します.乱数を固定した場合,同じデータで学習した場合の演算結果が等しくなります. |
補足② 回帰問題
回帰問題を行う場合はターゲット変数に数値データを選択して,分析の種類に回帰を選択します.回帰問題では予測値が連続データとして算出されます.
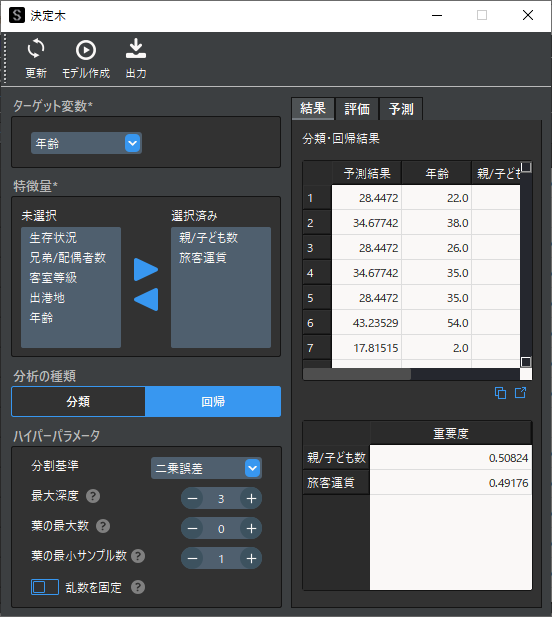
また,モデルの評価指標が分類問題とは異なりRMSE(平均平方二乗誤差)やMAE(平均絶対誤差)で評価します.これらの値は予測結果と実測値との誤差を示し,値が小さいほどモデルの予測精度が高いと言えます.
R²(決定係数)は0~1の間で算出され,1に近いほど当てはまりがよいとされます.
補足③ 発展的な手法
決定木の発展的な手法としてランダムフォレストや勾配ブースティング決定木があります.StaatAppを用いたこれらの手法の実践方法は以下のページで紹介しています.
》StaatAppで行うランダムフォレスト
》StaatAppで行う勾配ブースティング決定木
補足④ 決定木のアルゴリズム
StaatAppでは決定木のアルゴリズムとして,CART(Classification and Regression Tree)を利用しています.
また,演算処理としてはPythonで最も有名な機械学習用ライブラリのscikit-learnを使用しています.公式ドキュメントは以下になります.ドキュメント内にアルゴリズムの引用論文なども記載されているため,学術研究で記載する際は参考にしてください.
・分類問題(sklearn.tree.DecisionTreeClassifier)
・回帰問題(sklearn.tree.DecisionTreeRegressor)










