ノンパラメトリック検定であるマンホイットニーのU検定(ウィルコクソンの順位和検定)について,小標本の場合について解説します.
マンホイットニーのU検定とは
マンホイットニーのU検定とは,対応のない2群の差の検定(対応のないt検定)のノンパラメトリック版です.順序尺度以上のデータに対して用いることができます.
ウィルコクソンの順位和検定と呼ばれることもありますが,手法自体は同じです.(化学者のF・ウィルコクソンと,経済学者のH・B・マンと大学院生のホイットニーが同年代にそれぞれで考え出された手法になります.)
マンホイットニーのU検定の考え方は以下になります.
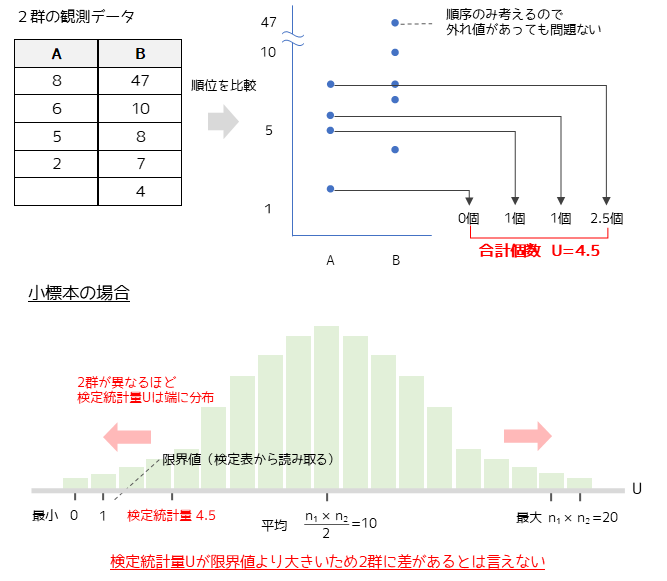
マンホイットニーのU検定では,2群のデータを順番に並べて順位を比較します.片方の群の値以下のもう片方の値の個数を,合計した値が検定統計量Uになります.
小標本の場合は検定統計量は専用の分布に従い,2群に差があるほど端に分布します.小標本とは両群のサンプルサイズがともに20以下,もしくは片方が7以下の場合です.
検定表から読み取った限界値と比較して,検定統計量が小さい場合(端に分布する)は,2群に差があると判定します.
マンホイットニーのU検定の手順
マンホイットニーのU検定は以下の手順で行います.
① 仮説の設定
帰無仮説は「2群の母集団に差がない」,対立仮説は「2群の母集団に差がある」として設定します.
② 有意水準の決定
有意水準α=0.05,もしくは0.01とします.一般的には有意水準α=0.05として設定されます.
③ 検定統計量の算出
具体的な計算手順は,Excelを用いた方法で解説しています.
④ 有意差判定
・検定統計量<限界値であれば,帰無仮説は棄却されて対立仮説を採択 → 「2群の母集団に差がある」
・検定統計量\(\geq\)限界値であれば,帰無仮説は棄却されない → 「2群の母集団に差があるとは言えない」
仮説検定の考え方や用語については,以下のページで解説しています.
検定結果を間違いたくない方へ
Excelを用いた計算方法より手軽・正確に,マンホイットニーのU検定の検定結果を調べることができる統計解析アプリStaatAppを販売しております.StaatAppでは標本数によって最適な計算方法でマンホイットニーのU検定が実行され,p値や効果量を求めることができます.
StaatAppではマンホイットニーのU検定以外にも,様々なノンパラメトリック検定・統計手法をマウス操作だけで実行することができます.詳細は以下のページをお読みください.
》StaatAppで行う仮説検定
》統計解析アプリStaatApp
例題で用いるデータと仮説の設定
例題では以下のサンプルデータを用います.AクラスとBクラスのテストの点数になります.
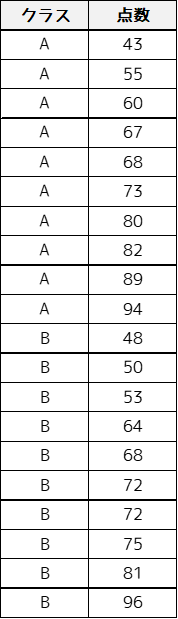
帰無仮説は「2つのクラスの点数に差がない」となり,対立仮説は「2つのクラスの点数に差がある」と設定します.
有意水準α=0.05で検定は行います.
Excelを用いた計算手順
Excelを用いた検定統計量の計算手順について説明します.
以下のような表を作成して,検定統計量Uを求めます.
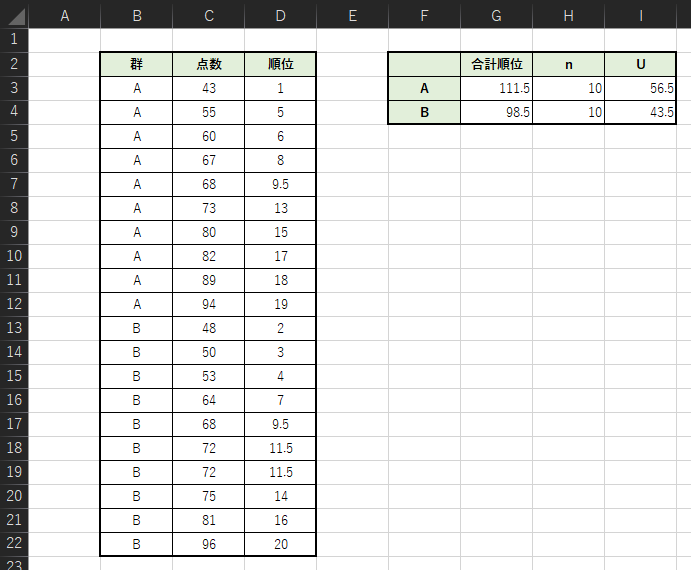
各セルの入力式は以下のようになります.
・D列:=RANK.AVG(C3,C:C,1) ※3行目のセルの数式です.下の行へは数式のコピーを行ってください.
・G3:=SUMIFS(D:D,B:B,F3)
・H3:=COUNTIFS(B:B,F3)
・I3:=G3-(H3*(H3+1))/2
入力式と計算手順について解説します.
① データの入力【B列】【C列】
群(クラス)と値(点数)を各1列にデータを入力します.
② 順位を求める【D列】
値を順位データに変換します.
順位データはRANK.AVG関数を用いて計算します.RANK.AVG関数の引数は以下になります.
RANK.AVG(“順位に変換する値”,”順位の対象となるデータ群(列)”,0)
※ 例題では値が小さいほど順位が高くなるように計算しています.
③ 各群の合計順位を求める【G3】【G4】
検定統計量の計算に必要な各群の合計値(順位和)を計算します.
特定の列の値ごとに合計値を計算するために,SUMIFS関数を用います.SUMIFS関数の引数は以下になります.
SUMIFS(“合計する値の範囲(列)”,”合計するか判定する値の範囲(列)”,”判定する値の範囲と一致させる値”)
④ サンプルサイズを求める【H3】【H4】
各群のサンプルサイズ(データ数)を求めます.COUNTIFS関数を用いて,「B列」に”A”と”B”がいくつあるかカウントします.
⑤ 検定統計量Uを求める
2群に対して以下の式で求めた値のうち小さい方が検定統計量Uになります.
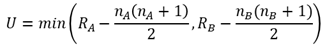
Riは各群の順位和,niはサンプルサイズになります.
例題では,56.5と43.5という値が計算できたので検定統計量U=43.5になります.
検定表から限界値の求め方
限界値の求め方について説明します.
例題では有意水準α=0.05であったので,両側5%の検定表を見ます.以下は検定表の一部抜粋です.
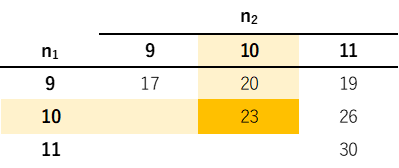
Aクラスのサンプルサイズは10であったのでn1=10となります.Bクラスのサンプルサイズも10であったのでn2=10となります.それぞれの行・列に一致する値である23が限界値となります.
※ サンプルサイズが等しくない場合は,サンプルサイズが小さい方をn1とします.
検定統計量が43.5であったため,検定統計量\(\geq\)限界値となり「2つのクラスの点数に差があるとは言えない」といった結論になります.
補足① マンホイットニー検定表
マンホイットニー検定表は以下になります.
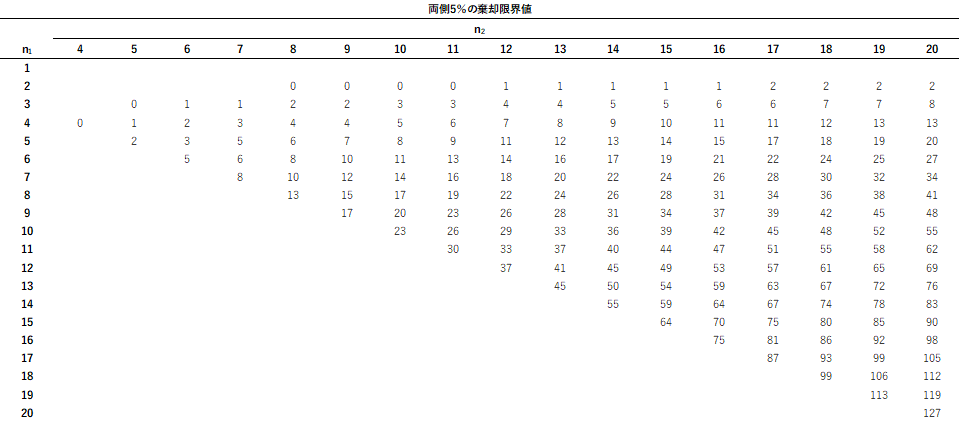
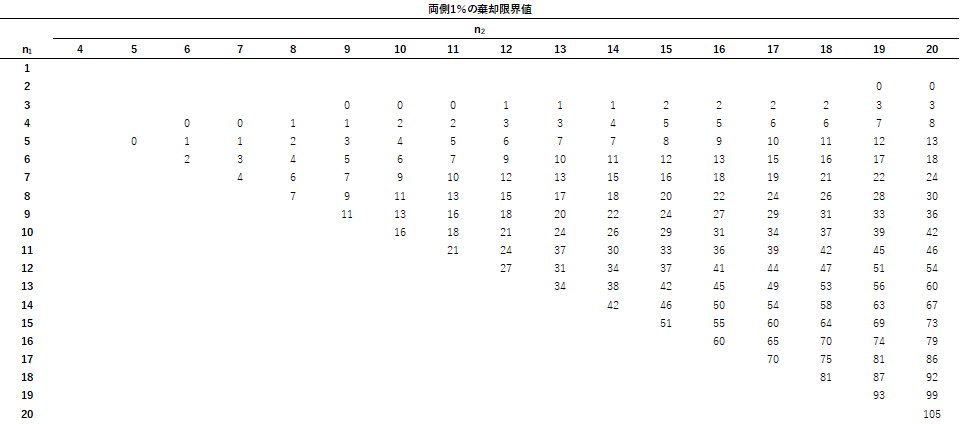
補足② 効果量の求め方(Excel版)
仮説検定の結果として重要な効果量の求め方について,Excelを用いて解説します.
ノンパラメトリック検定の効果量rは,以下の式で求めることができます.
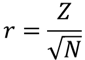
効果量と検定力分析入門 水本・竹内(2010)
※ 効果量には様々な計算方法があるため,論文などでは引用元もしくは計算式を示す必要があります.
Zは検定統計量を標準化(Z変換)した値,Nはサンプルサイズになります.マンホイットニーのU検定のU検定統計量Uは以下の式で標準化することができます.(詳しくは大標本の場合の計算手順で解説しています.)
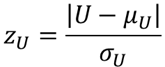
μUはU値の平均,σUはU値の標準偏差になります.Excelでは以下のように計算することができます.
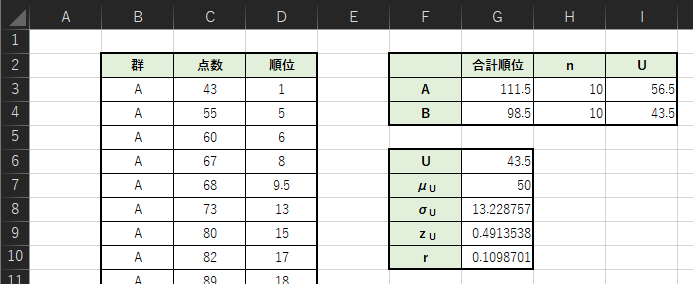
・G7セル:=H3*H4/2
・G8セル:=SQRT(H3*H4*(H3+H4+1)/12)
・G9セル:=ABS((G6-G7))/G8
※ より正確に標準偏差を求める際は,大標本の計算手順と同様に同順位の補正を行います.
・G10セル:=G9/SQRT(H3+H4)
効果量rの値の目安としては次のようになります.
【効果量rの目安】 小:0.1 中:0.3 大:0.5
例題において効果量は小さいため,「2つのクラスの点数にはそれほど差がない」と言うことができます.
補足③ サンプルサイズが大きい場合
小標本の(=サンプルサイズが小さい)データに対して行うマンホイットニーのU検定を紹介しました.大標本のデータに対しては検定統計量Uの正規化を行い,z検定します.
サンプルサイズが小さい場合の目安としては,両群のサンプルサイズがともに20以下,もしくは片方が7以下の場合です.
例えば,片方のデータの個数が21だった場合は,正規化近似を使ったマンホイットニーのU検定(ウィルコクソンの順位和検定)を行ってください.
大標本に対して行なうマンホイットニーのU検定の具体的な手順については,下記ページで解説しています.
補足④ データの前提条件
補足③に加えて,用いるデータの前提条件を解説します.
① ノンパラメトリックなデータ
マンホイットニーのU検定は,ノンパラメトリックな(=正規分布でない)データに対して行います.用いるデータが正規分布と仮定できる場合は,マンホイットニーのU検定を行うことも可能ですが,多くの場合で対応のないt検定を行います.(検定力がt検定に比べて95%であるため,t検定を用いることが多いです.)
② 順序尺度
名義尺度のデータに対しては用いることができません.名義尺度はデータの大小に意味が無い,つまり順位和を求めることができないことから明らかです.名義尺度のデータの差や関連性を分析する場合は,クロス集計表を用います.
③ 対応のないデータ
比較する2つのグループは対応のない場合である(異なる個体のデータ)である必要があります.対応のある場合は,ウィルコクソンの符号順位検定を行います.
④ 等分散性があるデータ
比較する2つのデータの分布(特に分散)が異なる場合,マンホイットニーのU検定は正確に検定することができません.分布が等しくない場合,ブルンナー・ムンチェル検定を行います.










