因子分析の具体的な計算方法について,PythonのFactorAnalyzerライブラリを用いて解説します.
補足事項として結果の見方や扱うデータの前提条件,プログラムを実行するための準備方法についても解説しています.
プログラミング不要,マウス操作で因子分析を実行できる統計ソフトについてはこちら.
因子分析の手順
因子分析は以下の手順で行います.
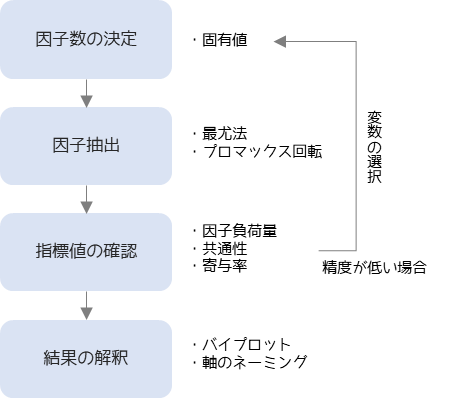
因子分析は分析前に因子数を決めます.因子数を決定する参考値としては,固有値(2以上の数)を用います.
因子抽出(分析の実行)では因子数分の因子を抽出します.因子の抽出方法としては一般的に最尤法が,軸の回転方法としてはプロマックス回転が使われます.
分析結果として抽出した因子・観測変数ごとの因子負荷量・共通性・寄与率を確認します.精度が低いと判断した場合は不要な観測変数を取り除いたり,軸の回転方法を変更して再度因子分析を行います.
因子分析の結果の解釈にはバイプロットを用いられます.バイプロットから軸のネーミングを行うことで,観測変数に隠れた潜在意識や根本原因を推測を行います.
例題の設定
因子分析を用いた統計解析を説明するために,以下の例題を用います.
社会人1年目の20人に対して,アンケートを取りました.回答者には仕事の悩みを5段階(1:当てはまらないー5:当てはまる)で評価してもらい,回答結果に対して因子分析を行います.
因子分析に用いる変数(アンケート項目)は以下の通りです.
x1:残業が多い
x2:仕事にやりがいを感じない
x3:給料が少ない
x4:休みが少ない,または取りにくい
x5:単純作業が多くスキルアップする見込みがない
x6:業務量が多い
x7:やりたい仕事をさせてもらえない
x8:人間関係がうまくいかない
以下のデータを用いて因子分析を行います.(1つの行で1人の回答結果を入力します.)
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 |
|---|---|---|---|---|---|---|---|
| 2 | 4 | 4 | 1 | 3 | 2 | 2 | 1 |
| 5 | 2 | 1 | 3 | 1 | 4 | 2 | 1 |
| 2 | 3 | 4 | 3 | 4 | 2 | 4 | 5 |
| 2 | 2 | 2 | 2 | 3 | 2 | 2 | 2 |
| 5 | 4 | 3 | 4 | 4 | 5 | 4 | 3 |
| 1 | 4 | 4 | 2 | 4 | 3 | 2 | 3 |
| 3 | 1 | 1 | 1 | 1 | 2 | 1 | 1 |
| 5 | 5 | 3 | 5 | 4 | 5 | 3 | 5 |
| 1 | 3 | 4 | 1 | 3 | 1 | 3 | 1 |
| 4 | 4 | 3 | 1 | 4 | 4 | 2 | 1 |
| 3 | 3 | 3 | 2 | 4 | 4 | 4 | 2 |
| 1 | 2 | 1 | 3 | 1 | 1 | 1 | 1 |
| 5 | 2 | 3 | 5 | 2 | 5 | 1 | 3 |
| 4 | 1 | 1 | 3 | 1 | 2 | 2 | 1 |
| 1 | 1 | 1 | 1 | 2 | 1 | 2 | 1 |
| 3 | 1 | 2 | 1 | 1 | 3 | 2 | 1 |
| 1 | 2 | 3 | 5 | 2 | 2 | 2 | 2 |
| 3 | 1 | 1 | 3 | 2 | 4 | 2 | 1 |
| 3 | 2 | 3 | 2 | 2 | 2 | 2 | 5 |
| 1 | 4 | 3 | 1 | 4 | 3 | 5 | 3 |
Pythonで読み込むせるデータ形式(CSVファイル)の作り方はこちら.
手順① 因子数の決定(固有値の計算)
Pythonを用いてプログラムの作成をします.
因子分析に必要なライブラリのインポートから因子数の決定まで行います.プログラムの記述内容は以下の通りです.
# ライブラリのインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
from factor_analyzer import FactorAnalyzer
# データの読み込み
df_workers = pd.read_csv("sample_factor.csv")
# 変数の標準化
df_workers_std = df_workers.apply(lambda x: (x-x.mean())/x.std(), axis=0)
# 固有値を求める
ei = np.linalg.eigvals(df_workers.corr())
print(ei)それぞれの記述内容について解説します.
① ライブラリのインポート
因子分析で用いるライブラリをインポートします.
5つのライブラリをインポートしますが,記述例と全く同じ内容で問題ありません.
# ライブラリのインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
from factor_analyzer import FactorAnalyzer② データの読み込み
pd.read_csv関数を用いて準備②で保存したCSVファイルの読み込み,データフレームに格納します.
データフレーム名(=の左側)は任意の値を入力します.””内は読み込むCSVファイル名を記述します.
# データの読み込み
df_workers = pd.read_csv("sample_factor.csv")③ 変数の標準化
各項目の分散による影響を無くすため変数の標準化を行います.
”データフレーム名”.apply(lambda x: (x-x.mean())/x.std(), axis=0)
という式で標準化が行えます.
# 変数の標準化
df_workers_std = df_workers.apply(lambda x: (x-x.mean())/x.std(), axis=0)④ 固有値の計算
因子数を決定するために,読み込んだ変数の相関行列の固有値を求めます.データフレームの相関行列はcorr関数で求めることができます.
固有値はnumpyライブラリのlinalg.eigvals関数で求めます.
# 固有値を求める
ei = np.linalg.eigvals(df_workers.corr())
print(ei)ここまで記述したらプログラムを実行します.PyCharmを用いている方は右上の「▶」ボタンを押すとプログラムが実行されます.
出力結果は以下のようになります.
[3.61634475 2.11925085 0.87875762 0.5678116 0.37337846 0.08163572 0.15971804 0.20310295]変数の数だけ固有値が計算されます.例題では8つ計算されます.
因子数は1以上の固有値の数となるので,計算結果から因子数は2となります.
手順② 分析の実行
求めた因子数に従って因子分析を行います.ここからのプログラムは手順①の続きに記述してください.全記述内容は以下になります.
# 因子分析の実行
fa = FactorAnalyzer(n_factors=2, rotation="promax")
fa.fit(df_workers_std)
# 因子負荷量,共通性
loadings_df = pd.DataFrame(fa.loadings_, columns=["第1因子", "第2因子"])
loadings_df.index = df_workers.columns
loadings_df["共通性"] = fa.get_communalities()
print(loadings_df)
# 因子負荷量の二乗和,寄与率,累積寄与率
var = fa.get_factor_variance()
df_var = pd.DataFrame(list(zip(var[0], var[1], var[2])),
index=["第1因子", "第2因子"],
columns=["因子負荷量の二乗和", "寄与率", "累積寄与率"])
print(df_var.T)
# バイプロットの作図
score = fa.transform(df_workers_std)
coeff = fa.loadings_.T
fa1 = 0
fa2 = 1
labels = df_workers.columns
annotations = df_workers.index
xs = score[:, fa1]
ys = score[:, fa2]
n = score.shape[1]
scalex = 1.0 / (xs.max() - xs.min())
scaley = 1.0 / (ys.max() - ys.min())
X = xs * scalex
Y = ys * scaley
for i, label in enumerate(annotations):
plt.annotate(label, (X[i], Y[i]))
for j in range(coeff.shape[1]):
plt.arrow(0, 0, coeff[fa1, j], coeff[fa2, j], color='r', alpha=0.5,
head_width=0.03, head_length=0.015)
plt.text(coeff[fa1, j] * 1.15, coeff[fa2, j] * 1.15, labels[j], color='r',
ha='center', va='center')
plt.xlim(-1, 1)
plt.ylim(-1, 1)
plt.xlabel("第1因子")
plt.ylabel("第2因子")
plt.grid()
plt.show()① 因子分析の実行
因子分析を実行します.因子分析はFactorAnalyzerモジュールを用いて行います.
2行目でFactorAnalyzerクラスを呼び出します.呼び出す際の引数は以下の通りです.
n_factors:因子数を設定します.デフォルトは3です.
rotation:軸の回転方法を設定します.例ではプロマックス回転を設定しています.詳しくは補足①をお読みください.
3行目でfitメソッドの引数として変数を標準化したデータフレームを渡して,因子分析が実行されます.
# 因子分析の実行
fa = FactorAnalyzer(n_factors=2, rotation="promax")
fa.fit(df_workers_std)② 因子負荷量・共通性を求める
因子分析の結果として重要な因子負荷量と共通性を計算します.
因子負荷量はloadings_メソッドを用いて計算することができます.2行目で計算した因子負荷量を画面出力用のデータフレームに格納します.引数のcolunmsは因子数に合わせて記述してください(因子数が3の場合は,”第3因子”を追記).
3行目では画面出力用データフレームのカラム名(行名)に変数名を追加しています.
共通性はget_communalitiesメソッドを用います.4行目で画面出力用データフレームに新しい列として共通性の計算結果を追加します.
# 因子負荷量,共通性
loadings_df = pd.DataFrame(fa.loadings_, columns=["第1因子", "第2因子"])
loadings_df.index = df_workers.columns
loadings_df["共通性"] = fa.get_communalities()
print(loadings_df)プログラムを実行後の出力結果は以下のようになります.
第1因子 第2因子 共通性
x1 -0.196394 0.917136 0.879709
x2 0.859422 0.067413 0.743150
x3 0.829155 -0.161144 0.713466
x4 -0.017808 0.558695 0.312457
x5 0.984061 -0.063608 0.972421
x6 0.180765 0.850078 0.755308
x7 0.680743 -0.064480 0.467569
x8 0.532039 0.221023 0.331916変数ごとに因子負荷量と共通性が出力されます.
因子負荷量は各因子に関係性が深い変数ほど値が大きくなり,-1から1の間の値を取ります.第1因子はx5(単純作業が多くスキルアップする見込みがない)の因子負荷量が最も大きいためx5と関連性が深い因子と言うことができます.
第2因子はx1(残業が多い)とx6(業務量が多い)の情報を多く含んでいます.
共通性は各変数の持つ情報が因子モデルにどれだけ反映されているかを示しています.共通性の小さい変数は因子モデルから削除して,再度因子分析を行うとより良い結果を得ることができます.
x4やx8は共通性が比較的低いため,あまり因子モデルに情報が反映されていないと言えます.
③ 各主成分への寄与率と累積寄与率を求める
因子分析で計算した各因子に対して,寄与率と累積寄与率を求めます.寄与率とは,各因子がどれだけの情報を説明できているかという指標になります.
# 因子負荷量の二乗和,寄与率,累積寄与率
var = fa.get_factor_variance()
df_var = pd.DataFrame(list(zip(var[0], var[1], var[2])),
index=["第1因子", "第2因子"],
columns=["因子負荷量の二乗和", "寄与率", "累積寄与率"])
print(df_var.T)寄与率と累積寄与率はget_factor_variance()で求めることができます.
3行目と4行目で画面出力用のデータフレームに計算結果を格納しています.
5行目で画面出力用データフレームを転置して出力します.出力結果は以下になります.
第1因子 第2因子
因子負荷量の二乗和 3.212520 1.963477
寄与率 0.401565 0.245435
累積寄与率 0.401565 0.647000第1因子の寄与率は約40%,第2因子の寄与率は約25%であり合せて約65%であることが分かります.
累積寄与率は60%を超えるとよいとされています.
④ バイプロットを作図する
バイプロットは各因子の因子負荷量のベクトル表記と,因子得点をプロットした図になります.例題では第1因子を横軸に第2因子を縦軸にしたバイプロットを作成します.
※ 因子得点とはアンケート回答者(サンプル)の回答結果を各因子で再計算した値になります.
バイプロット図は,matplotlibライブラリのpyplotモジュールを用いて作図します.自分の環境で実行する際に最低限修正が必要な行は以下になります.
2行目:transform(変数を標準化したデータフレーム名)
6行目:データフレーム名.colonms
7行目:データフレーム名.index
因子得点の分布は16行目のannotateメソッド,因子負荷量は18行目のarrowメソッドでベクトル表記,19行目のtextメソッドで変数名を描画しています.
メソッド内の引数を変更することで,バイプロット上での表現(矢印の大きさや色など)を変更することができます.
# バイプロットの作図
score = fa.transform(df_workers_std)
coeff = fa.loadings_.T
fa1 = 0
fa2 = 1
labels = df_workers.columns
annotations = df_workers.index
xs = score[:, fa1]
ys = score[:, fa2]
n = score.shape[1]
scalex = 1.0 / (xs.max() - xs.min())
scaley = 1.0 / (ys.max() - ys.min())
X = xs * scalex
Y = ys * scaley
for i, label in enumerate(annotations):
plt.annotate(label, (X[i], Y[i]))
for j in range(coeff.shape[1]):
plt.arrow(0, 0, coeff[fa1, j], coeff[fa2, j], color='r', alpha=0.5,
head_width=0.03, head_length=0.015)
plt.text(coeff[fa1, j] * 1.15, coeff[fa2, j] * 1.15, labels[j], color='r',
ha='center', va='center')
plt.xlim(-1, 1)
plt.ylim(-1, 1)
plt.xlabel("第1因子")
plt.ylabel("第2因子")
plt.grid()
plt.show()出力結果は以下になります.
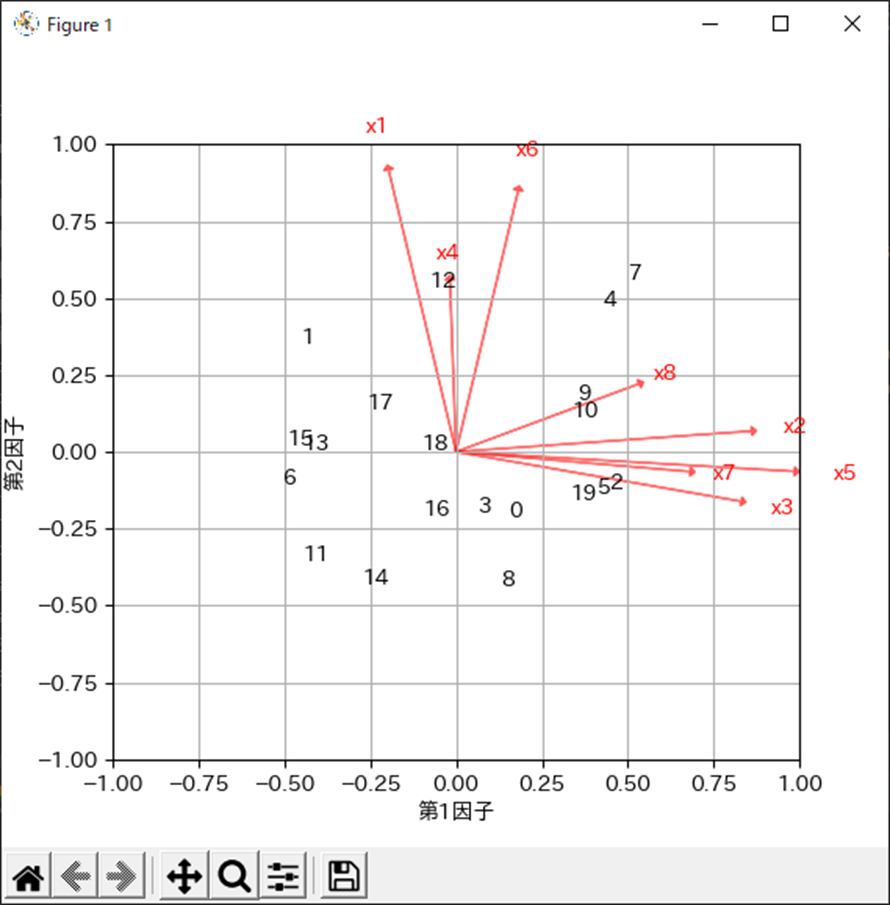
バイプロットから第1因子に強く相関がある変数は,x2,x3,x5であることがわかります.
因子得点の分布からはサンプル番号12の人は第2因子の得点が高く,7の人は第1因子と第2因子の両方の得点が高いことがわかります.
手順③ 結果の解釈(軸のネーミング)
因子分析の結果は各因子に名前をつける(軸のネーミング)ことで解釈を行います.各因子との相関の度合いを表す因子負荷量を見ることで因子に名前を付けます.
因子負荷量から第1因子に強い相関を持つ変数は以下となります.
x2:仕事にやりがいを感じない
x3:給料が少ない
x4:単純作業が多くスキルアップする見込みがない
x7:やりたい仕事をさせてもらえない
各変数から共通点として,”仕事に対するやる気が低い”ということがわかります.よって第1因子は”やる気の低さ”と名前を付けます.
同様に,第2因子に強い相関をもつ変数は以下になります.
x1:残業が多い
x4:休みが少ない,または取りにくい
x6:業務量が多い
各変数から共通点として,”働く時間が長い”ということがわかります.よって第2因子は”仕事時間”と名前を付けます.
第1因子と第2因子に名前を付けたことで,アンケート結果の解釈を質問項目以外の観点から行うことができます.
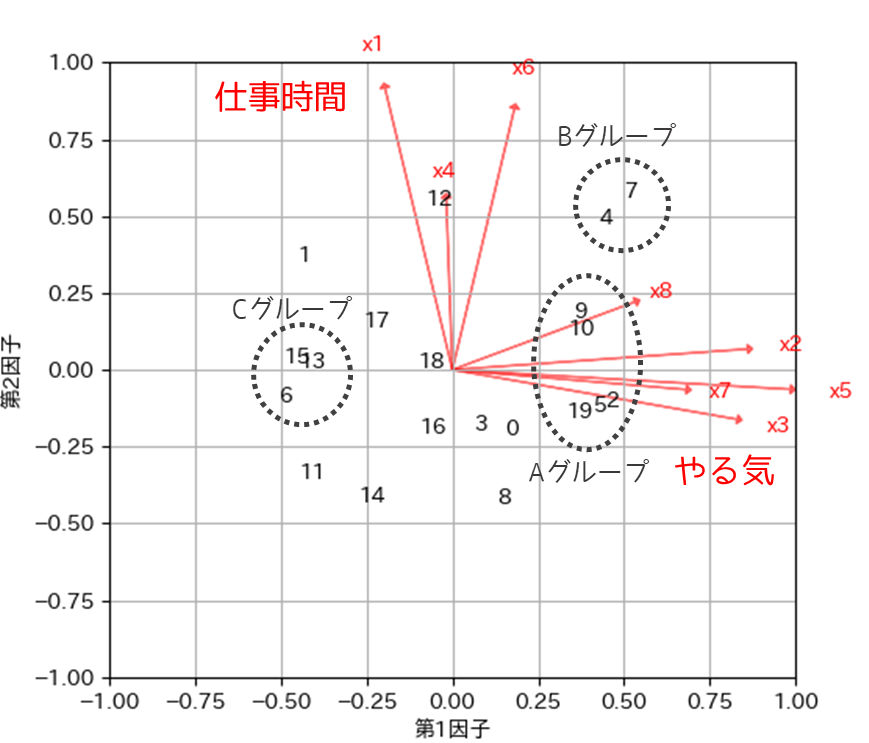
バイプロットにおいて,Aグループの位置にプロットされた人は仕事に対するやる気が低く,Cグループの位置にプロットされた人はやる気が比較的高いと解釈することができます.
Bグループの位置にプロットされている人は,やる気が低く仕事時間も長いと解釈することができます.
因子負荷量に目立った傾向がない場合は,軸の回転を行い当てはまりのよい軸(因子)を見つけます.詳しくは補足①をお読みください.
補足① 軸の回転とは
軸の回転とは,変数に対して因子の当てはまりが良くなるように原点を中心に座標軸を回転させることです.
2つの軸がなるべく変数に重なるように回転させることで,変数ごとの因子負荷量が大きくなり因子の特徴を捉えやすくなります.
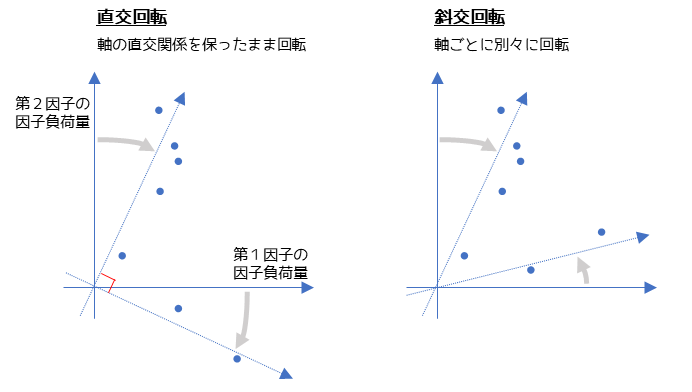
軸の回転基準を設定する方法には,直交回転と斜交回転の2つがあります.直交回転は因子間の相関を仮定しないモデルで,斜交回転は因子間の相関を仮定するモデルになります.データによっては斜交回転を行っても相関がほとんどない場合もあります.
回転基準としてよく使われるのは斜交回転になります.斜交回転の方が柔軟なモデリングを行える分,より単純構造に近づく(因子の特徴が説明しやすくなる)からです.特に今回のような,心理学が関わる因子分析でよく用いられます.
斜交回転の中ではプロマックス回転が論文などでもよく使われます.
FactorAnalyzerクラスの引数rotationに設定することができる回転基準は以下になります.
| 値 | 名称 | 分類 | 備考 |
| varimax | バリマックス | 直交 | 直交回転で最も代表的な手法. |
| oblimax | オブリマックス | 直交 | |
| quartimax | クォーティマックス | 直交 | |
| equamax | エカマックス | 直交 | バリマックスとクォーティマックスの組み合わせ手法 |
| promax | プロマックス | 斜交 | 斜交回転で最も代表的な手法(デフォルト). |
| oblimin | オブリミン | 斜交 | 単純構造にならないと思わるデータに有効. 恐らくコバリミン基準で計算している. |
| quartimin | クォーティミン | 斜交 | オブリミン基準の一種. |
単純構造とは複数の変数の因子負荷量の値は大きく,それ以外の変数の値は0.5を下回る小さい値になることです.因子分析の結果が単純構造となると,因子負荷量にメリハリができ特徴ある因子を得られたという結果になります.
補足② 統計解析アプリ
本サイトではより手軽に因子分析を実行して,寄与率・因子負荷量・共通性の算出・バイプロットの作成を行うアプリ(StaatApp)を販売しています.
詳細は以下のページで紹介しています.
》StaatAppで行う因子分析
》統計解析アプリStaatAppとは
補足③ 因子分析とは
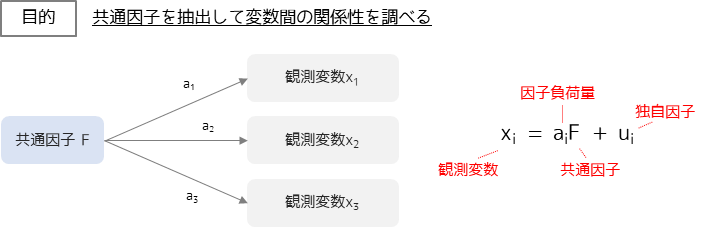
因子分析とは,変数に共通して影響を与えている概念(共通因子)を抽出して変数間の関係性を調べる多変量解析の1つです.
観測変数と因子負荷量,共通因子の関係は図のようになります.観測変数は因子負荷量と共通因子の積に独自因子を加えた値であると定義して,因子負荷量・共通因子を求めます.
補足④ 因子分析を行う前提条件
因子分析で扱うデータは,以下の2つの条件に注意してください.
① 量的データ
因子分析の対象データは量的データである必要があります.アンケートの調査結果などで質的データを含んでいるデータを扱う場合は,ダミー変数を用いる必要があります.
② サンプル数が説明変数より多い
因子分析はサンプル数が説明変数の数より多い必要があります.
補足⑤ PyCharmを用いた実行環境の構築
Pythonを初めて使う方や,自分のPCにPython・PyCharmが入っていない方は以下のページで解説している手順で実行環境の構築を行ってください.
初めて触る方にもわかりやすいようにPyCharmを用いた手順となっています.因子分析では,”FactorAnalyzer”というライブラリを使用します.インストール方法が分からない方は,ライブラリのインストールを参考にしてください.
》実行環境の構築方法【Pycharm使用】
》ライブラリのインストール方法【Pycharm使用】
補足⑥ Pythonで読み込むデータの作成方法
Pythonで扱うCSVファイルの作成方法は以下のページで解説しています.










