統計的因果推論の1つである層別解析について,考え方や使い方を図と例題を用いて解説します.
サブグループ解析との違いや,よくある間違いについても解説しています.
層別解析とは

層別解析とは比較する群をサンプルの属性(変数)ごとに分割して,分割したグループ(層)ごとに分析を行う解析手法になります.
層別解析を行うことで群ごとの比較では見つけることができなかった群間の差や,変数による影響を調べることができます.
層別解析の具体例
社会人21人に関する以下のようなデータがあるとします.

このデータから副業している人としていない人の2群に対して,年収の比較を行うとします.通常の仮説検定であれば対応のないt検定を行い,有意差があれば副業の有無は年収に影響を与えていると判定することができます.
ただし単純に仮説検定を行った場合には,年齢といった年収に影響を与えている影響(交絡因子)を取り除かずに比較を行っているという問題点があります.例えば,年収は年齢に比例して高くなる傾向があり,副業している人は年齢が低い傾向があるとします.この場合,副業している人と副業をしていない人で年収に差がないとしても,それは年齢による影響で,副業の有無によって差が生じていない可能性があります.
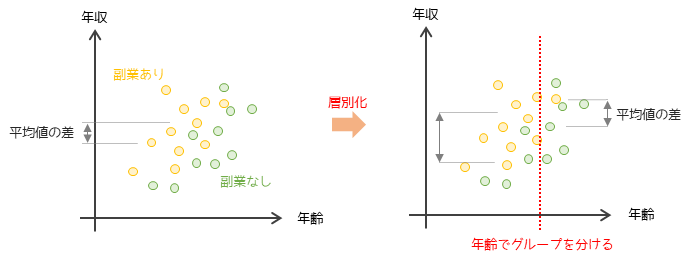
層別解析では特定に変数を基準に群内のサンプルをグループ化します.図では年齢の高低によって層別化を行っています.
単純に2群を比較するよりも,層別化したグループごとに2群を比較した方が差が明らかに増加していることがわかります.特に層別化することで,年齢が低い社会人は副業をしている人としていない人で年収に差があることがわかります.
このように層別解析では特定の交絡因子を基準にグループ分けを行うことで,交絡因子をできるだけ小さくすることができます.
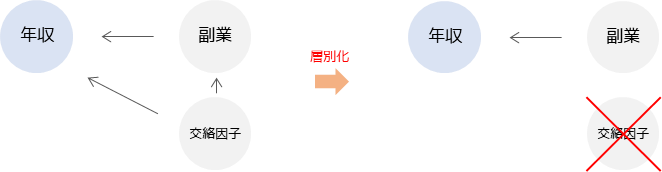
層別解析では最終的に各グループの結果の統合を行います.統合する方法として一般的なのは,重み付け平均を用いることです.分割した各グループのサンプルサイズや分散を用いて重み付け平均を計算します.
層別化したグループの分析方法は,仮説検定以外にも基本統計量や回帰分析など様々な手法を用いることが可能です.
デメリット
層別解析のデメリットについて紹介します.
① サンプルサイズが小さくなる
元のサンプルを分割するためサンプルサイズが必ず小さくなります.サンプルサイズが小さくなることで標準誤差が増加して効率が下がります.
② 数量データの場合,基準が恣意的になる
数量データは連続値であるため層別化するための基準値が恣意的になります.年齢を基準に層別化を行う場合,どの年齢を基準に分割するかは分析者の主観となってしまいます.
③ 共変量が複数ある場合に層別化できない
層別化の基準値には交絡因子となる変数(共変量)を用います.共変量が複数ある場合はどのように分割するか判断が複雑になり,層別化できません.
応用① サブグループ解析との違い
層別解析とよく似た手法としてサブグループ解析があります.サブグループ解析とは層別解析と同様に比較する群をいくつかのグループごと分割して比較する手法になります.
サブグループ解析と層別解析の違いは,グループごとの結果を統合するかどうかになります.層別解析では最終的に結果を統合して1つの結果として解釈を行います.サブグループ解析では各グループの結果で解釈を行います.
サブグループ解析は交互作用の有無を調べることが目的の1つでもあります.
応用② 層別解析のよくある間違い
層別解析を行った際によくあるのが,グループごとの解析結果をそのまま結論として用いることです.層別解析ではグループ分けによりサンプルサイズが小さくなるため,以下のような間違いが起きがちです.
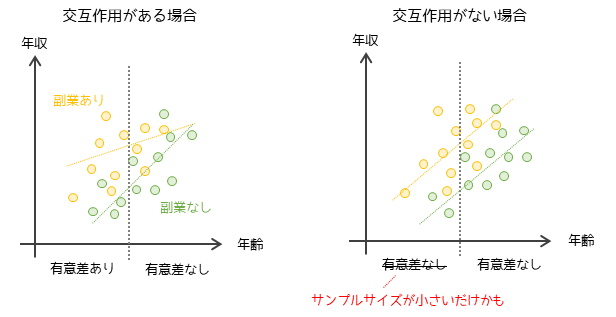
左の図は副業の有無と年齢に交互作用がある場合で,年齢が低い人の比較では有意差があり年齢が高い人の比較では有意差がないという結果になります.この結果は結論として用いても問題無さそうです.
右の図は副業の有無と年齢に交互作用がない場合で,仮説検定による比較結果は年齢が低い人でも有意差がなかったとします.しかし,年齢が低い人の比較ではサンプルサイズが小さいため有意差がなかった可能性があります.また,交互作用がない場合は共分散分析を用いる方が正しい結論を得やすいです.
仮説検定におけるp値はサンプルサイズが小さいほど,有意差が出にくくなるため層別化によってサンプルサイズを小さくすると本来ある差が判定されないということがあります.層別解析では結果から即断で結論を得るのではなくデータの性質・分布と照らし合わせることが重要です.
応用③ 層別サンプリング
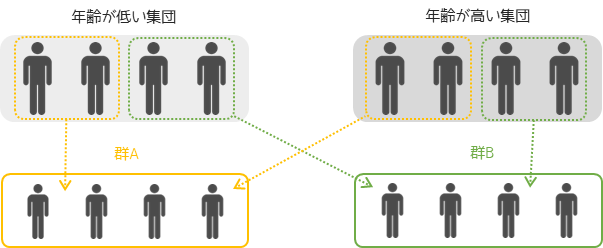
実験の標本作成段階で層別化を行うことを層別サンプリング(層別抽出)と言います.事前に年齢が年収に影響を与えている交絡因子であると判断できる場合,年齢という条件を均等に割り振ることで影響を排除することができます.
層別解析は本来であればこのような層別サンプリングを行い,群内のグループの分割が明確であるデータに対して用いる解析手法になります.
層別サンプリングを行わずに,後付で層別化を行う解析手法のことをサブグループ解析と言うこともあります.
応用④ 統計的因果推論
層別解析はランダム化比較試験を行わずに変数間の因果関係を示したい場合に,交絡によるバイアスを取り除くために行う統計的因果推論の1つです.
統計的因果推論の代表例としては,既に紹介した共分散分析の他に傾向スコアマッチングや差分の差分法という手法があります.
【主な因果推論】
・共分散分析
・傾向スコアマッチング
・差分の差分法









