交絡によるバイアスを取り除くために行う統計的因果推論の1つである,傾向スコアマッチングについて図を用いて解説します.
具体例を用いて傾向スコアの推定方法や手順についても解説しています.
傾向スコアマッチングとは
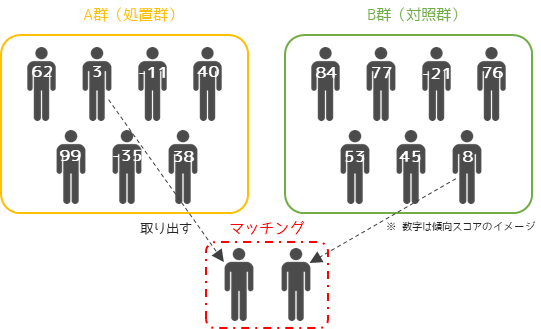
統計学において異なるサンプルで,似ている要素(交絡因子)をもつデータを見つけてペアにすることをマッチングと言います.
傾向スコアマッチングとは,マッチングの際のペアを見つける基準として傾向スコアを用いる手法になります.
一般的には傾向スコアは,目的変数を原因の変数(A群=1,B群=0)に説明変数を交絡因子にしてロジスティック回帰を行うことで求めます.
なぜ行うのか
傾向スコアマッチングはランダム化比較試験を行わずに変数間の因果関係を示したい場合に,交絡によるバイアスを取り除くために行います.(統計的因果推論)
具体的に年収と副業の関係を用いて説明します.副業が年収に影響を与えてるかを調べるために,副業している人(=処置群)の年収と副業していない人(=対照群)の年収で比較するとします.
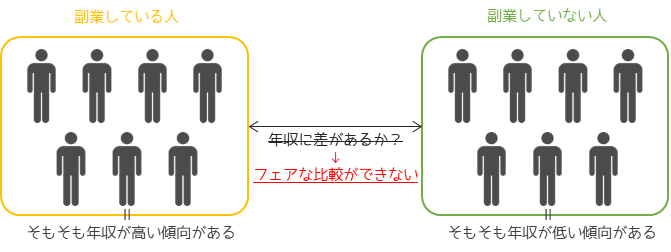
処置群にそもそも年収が高い傾向があったり,対照群に年収が低い傾向がある場合にフェアの比較を行うことができません.このような状況で副業をしている人の方が年収が高いと判定できた場合でも,それは副業以外の要因が影響していると考えることもできます.
このように比較したい要因以外の影響(交絡因子)を取り除くために,傾向スコアマッチングを行います.

傾向スコアマッチングでは元のサンプルから,マッチングを行うことで似ているデータを抽出します.抽出し直した新しい処置群と対照群を用いることで,交絡因子を除いたフェアな比較が可能になります.
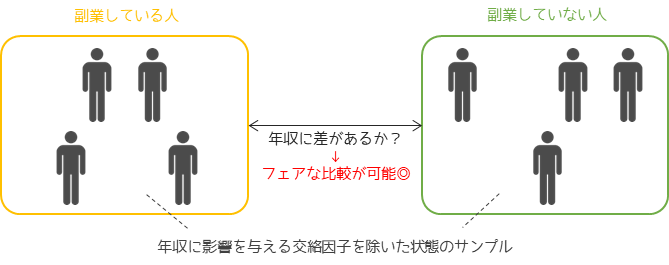
デメリット
傾向スコアマッチングは因果関係を調べる際に,有用な手法ですがデメリットがあります.
① サンプルサイズが小さくなる
元のサンプルから抽出して,新しいサンプルを作成するためサンプルサイズが必ず小さくなります.サンプルサイズが小さくなることで標準誤差が増加して効率が下がります.
② 他の統計的因果推論と比較して効率が良くない場合がある
統計的因果推論には傾向スコアマッチング以外に,共分散分析や層別解析があります.これらの手法と比較して必ずしも効率的とは言えません.
因みに他の統計的因果推論と比較した傾向スコアマッチングの最大のメリットは,比較的理解しやすい手法であるという点です.
傾向スコアマッチングの手順
傾向スコアマッチングは以下の手順で行います.
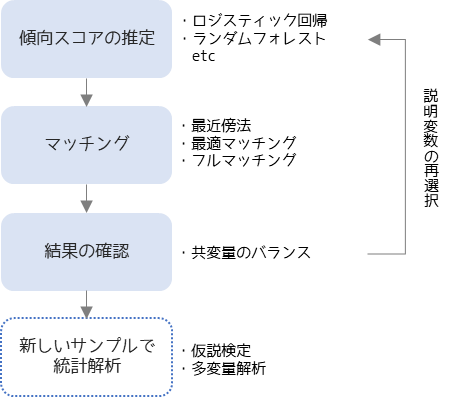
最初にロジスティック回帰分析などを行い,傾向スコアを計算します.
求めた傾向スコアからマッチングを行います.マッチング方法には最近傍法や最適マッチングといった方法があります.
マッチングを行い新しいサンプルを抽出したら,2群(処置群と対照群)に分けて共変量のバランスを確認します.バランスが取れていない場合は,交互作用項や2乗項を説明変数に加えて再度傾向スコアを計算します.
共変量のバランスが取れている場合は,新しいサンプルを用いて仮説検定や多変量解析のような統計解析を行います.
傾向スコアマッチングを行う方法
傾向スコアマッチングは複雑な計算が必要なため,Excelなどの手計算で行うことは難しいです.基本的にはRやPythonなどのプログラミング言語を用いて行う必要があります.
統計解析アプリStaatAppでは傾向スコアマッチングを,プログラミングを行わずクリック操作だけで扱うことができます.傾向スコアの算出ではロジスティック回帰や決定木など様々な方法を用いることができ,マッチング済みデータの分析方法も多様にあります.
StaatAppについてや具体的な方法は以下のページよりご覧ください.
》統計解析アプリStaatApp
》Staatappを用いた傾向スコアマッチング
傾向スコアの求め方
傾向スコアを求める方法で最も使われるのは,ロジスティック回帰になります.
以下のようなデータに対して,年収と副業の因果関係を調べるため傾向スコアを推定する場合は,副業を目的変数にその他の変数を説明変数としてロジスティック回帰を行います.
推定したモデル(回帰式)から算出される確率が傾向スコアになります.

ロジスティック回帰以外に傾向スコアを求める方法として,ランダムフォレストなどの機械学習のアルゴリズムが使われることがあります.
マッチング方法
傾向スコアを用いたマッチング方法としてよく使われるのが,強欲マッチングになります.強欲マッチングとは処置群の任意の個体で,傾向スコアが最も近い対照群の個体を逐次探索する方法です.
強欲マッチングの中でも最近傍法がよく使われます.
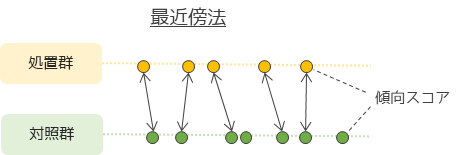
強欲マッチング以外では,最適マッチングやフルマッチング(完全一致)といった方法があります.最適マッチングでは処置群と対照群の各個体の傾向スコアの差(距離)の合計値が最小になるようにマッチングを行います.
補足① 統計的因果推論
傾向スコアマッチングはランダム化比較試験を行わずに変数間の因果関係を示したい場合に,交絡によるバイアスを取り除くために行う統計的因果推論の1つです.
統計的因果推論の代表例としては,傾向スコアマッチングの他に共分散分析や層別解析,差分の差分法という手法があります.










