分散分析と回帰分析を組み合わせた手法である共分散分析について,考え方や使い方を図を用いて解説します.
ExcelやPythonを用いた計算方法についても紹介しています.
共分散分析とは
共分散分析は仮説検定と同様に,群間の差を比較する解析手法です.群間の差を比較することで群を分けている要因の影響を調べることができます.
共分散分析の特徴は,調べたい要因以外の影響を取り除いて比較することができるため検出力を上げることができます.イメージとしては回帰分析+分散分析のような分析方法になります.
共分散分析はAncova(analysis of covariance)と表記されることもあります.
共分散分析の具体例
社会人21人に関する以下のようなデータがあるとします.

このデータから副業している人としていない人の2群に対して,年収の比較を行うとします.通常の仮説検定であれば対応のないt検定を行い,有意差があれば副業の有無は年収に影響を与えていると判定することができます.
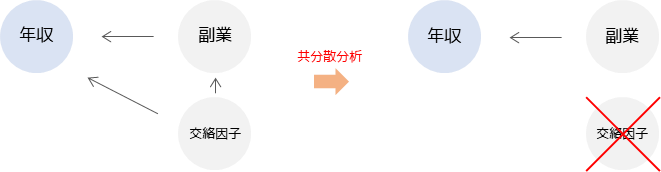
仮説検定を行った場合の問題点として,年齢といった年収に影響を与えている影響(交絡因子)を取り除かずに比較を行っている点です.例えば,年収は年齢に比例して高くなる傾向があり,副業している人は年齢が低い傾向があるとします.この場合,副業している人としていない人で年収に差がないとしても,それは年齢による影響で差が生じていない可能性があります.
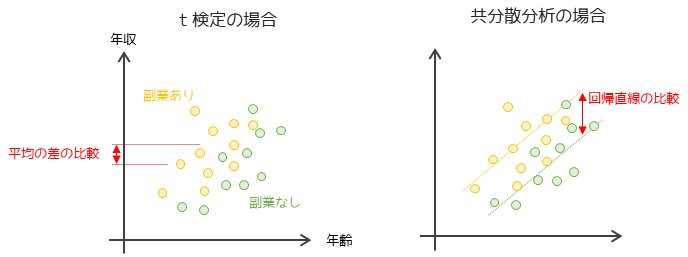
共分散分析では2群を平均値ではなく回帰直線で比較します.
図のように年収と年齢に関する回帰直線で比較することで年齢による影響を取り除いて,副業の有無のみが年収に与える影響(差)を調べることができます.
Excelを用いた共分散分析
Excelで行う共分散分析の方法について紹介します.用いるデータと分析目的は具体例と同様です.
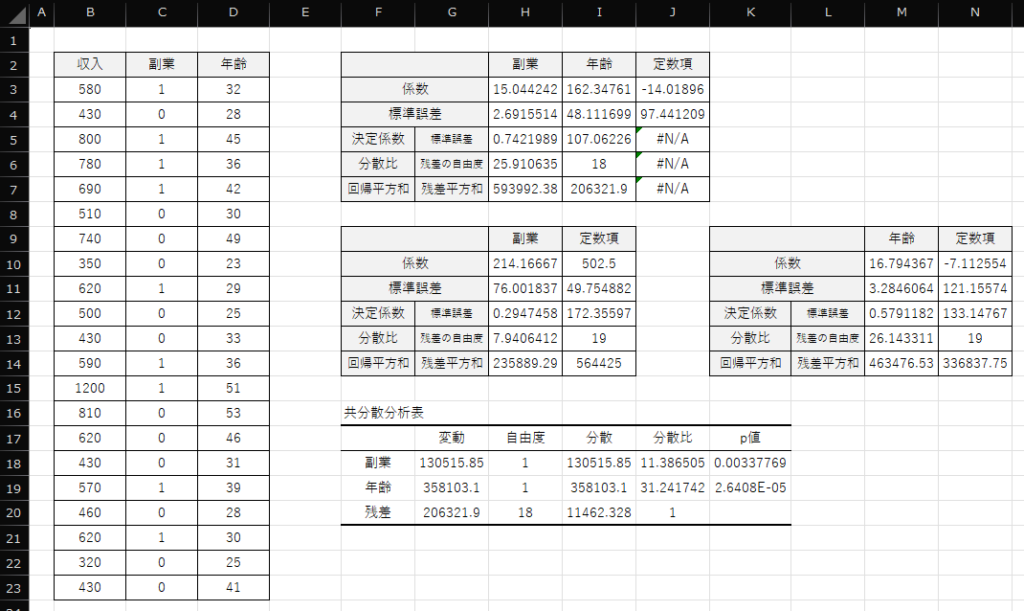
共分散分析は以下のように表を作成して行うことができます.カテゴリーデータ(副業の有無)はダミー変数に変換しています.
変数ごとに回帰分析を行い,算出した値を用いること(残差得点の分散分析)で共分散分析を行うことができます.詳細な手順は以下になります.
① 変数全体(主作用)で回帰分析を行う
対象の変数で回帰分析を行います.データ分析ツールで回帰分析を行うこともできますがここではLINEST関数を用いて回帰分析を行います.
LINEST関数の書き方:=LINEST(“目的変数の範囲”, “説明変数の範囲”, “定数項の有無”, “補正項の出力有無”)
目的変数には調べたい差を示す変数を選択します.例題では年収の差調べるため,年収の列を選択します.説明変数には目的変数以外の変数を選択します.
定数項の有無ではTRUEもしくは何も入力しません.補正項の出力有無はTRUEを入力します.
H3セルの入力例は以下のようになります.
=LINEST(B3:B23,C3:D23,,TRUE)
回帰分析の結果を表形式で出力するために,まずシート上の出力範囲を選択します.例題ではH3からJ7までのセルを選択状態にします.選択範囲は列数が目的変数+1,行数は5行になります.出力範囲が選択状態になったら選択範囲の左上のセル(H3セル)にLINEST関数を入力します.入力が完了したらCtrl+Shift+Enterを押します.
② 固定因子のみで回帰分析を行う
比較する群を示す名義尺度をダミー変数に変換した値(固定因子)のみで回帰分析を行います.
例題では固定因子は副業の有無になります.①と同様にLINEST関数を利用したH10セルの入力式例は以下のようになります.
=LINEST(B3:B23,C3:C23,,TRUE)
出力範囲の指定方法なども①と同様の方法で行ってください.
③ 共変量ごとに回帰分析を行う
交絡因子となる変数(共変量)ごとに回帰分析を行います.例題では共変量は年齢となり,M10セルへの入力式例は以下のようになります.
=LINEST(B3:B23,D3:D23,,TRUE)
共変量が複数ある場合は,繰り返し回帰分析を行い表を作成します.
④ 共分散分析表の作成
共分散分析表の作成を行い,p値を求めます.基本的な考え方は一元配置分散分析と同様です.
変動・自由度は以下のように求めます.
■ 変動
固定因子:共変量の残差平方和 – 主作用の残差平方和
共変量:固定因子の残差平方和 – 主作用の残差平方和
残差:主作用の残差平方和
■ 自由度
固定因子:群数 – 1
共変量:1
残差:サンプルサイズ – 群数
分散・分散比・p値は変動と自由度を用いて順次計算します.例題での計算式は以下のようになります.
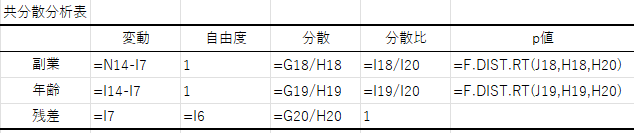
以上がExcelを用いた共分散分析の方法になります.
例題では共分散分析表から副業有無(固定因子)のp値<0.05であることがわかります.これは,「年収に対して年齢の影響を取り除いた場合でも,副業の有無によって年収に差がある」ということを意味します.
Pythonを用いた共分散分析
Pythonを用いた共分散分析の方法を紹介します.Pythonではpingouinライブラリのancova関数を用いることで簡単に共分散分析を行うことができます.
記述例は以下のようになります.Excelで説明したデータと同じ値をcsvファイルとして読み込んでいます.
# ライブラリのインポート
import pandas as pd
from pingouin import ancova
# データの読み込み
df_workers = pd.read_csv("ancova.csv")
# 共分散分析の実行
result = ancova(data=df_workers, dv="income", covar="age", between="side_job")
print(result)出力結果は以下のようになります.
Source SS DF F p-unc np2
0 side_job 130515.850475 1 11.386505 0.003378 0.387474
1 age 358103.096910 1 31.241742 0.000026 0.634456
2 Residual 206321.903090 18 NaN NaN NaNside_jobのp-uncが副業有無(固定因子)のp値になります.Excelでの計算例と一致していることがわかります.
詳細は公式ドキュメントをお読みください.Pythonを用いた統計解析全般は以下のページで解説しています.
応用① 共分散分析の前提条件
共分散分析を行うための前提条件について紹介します.母集団の分布の正規性や,等分散性は分散分析の前提条件と同じです.
分散分析の前提条件に加えて以下2つの前提条件は特に重要です.
① 実験変数と共変量に相関関係がある
実験変数(年収)と共変量(年齢)に相関関係があるかを事前に調べます.相関関係がない場合は共変量が実験変数に影響を与えておらず共分散分析を行う意味はありません.この場合は,対応のないt検定や一元配置分散分析を行います.
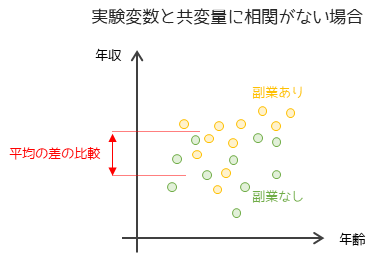
2変数の相関関係は,無相関の検定を行うことで調べることができます.
② 群ごとの回帰直線の傾きが等しい
群ごとの回帰直線の傾きが等しい(交互作用がない)場合に共分散分析を行うことができます.
回帰直線の傾きが非平行(等しくない)である場合は,統計学的には「各群(副業の有無)と共変量(年齢)には交互作用がある」と言います.交互作用がある場合は共分散分析で共変量の影響を除くことができず,年齢の高低ごとに分けて比較する層別解析を行う必要があります.
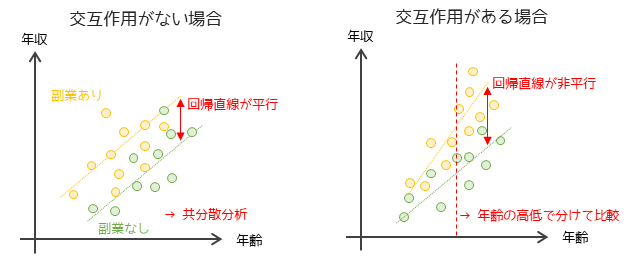
交互作用の有無は二元配置分散分析を行うことで調べることができます.
応用② 重回帰分析との違い
共分散分析は説明変数の1つにカテゴリーデータを加えた重回帰分析に相当します.
例題では目的変数を「年収」,説明変数を「副業の有無をダミー変数に変換した値」と「年齢」とした重回帰分析を行うことで,固定因子と共変量のp値を偏回帰係数のp値として求めることができます.
Excelにおいても共分散分析表のp値を求めたいだけであれば,データ分析ツールの回帰分析を行うことで求めることは可能です.
重回帰分析と同様に,共変量に多重共線性がある場合は共分散分析を行う前に取り除く必要があります.
応用③ 統計的因果推論
共分散分析はランダム化比較試験を行わずに変数間の因果関係を示したい場合に,交絡によるバイアスを取り除くために行う統計的因果推論の1つです.
統計的因果推論の代表例としては,既に紹介した層別解析の他に傾向スコアマッチングや差分の差分法という手法があります.傾向スコアマッチングについては以下のページで解説しています.
【主な因果推論】
・層別解析
・傾向スコアマッチング
・差分の差分法








