標準化とは
標準化とはデータの平均値を0,標準偏差(ばらつき)を1に変換することです.標準化した値は標準化変量と言います.
元データと偏差,標準化変量の関係は以下のようになります.
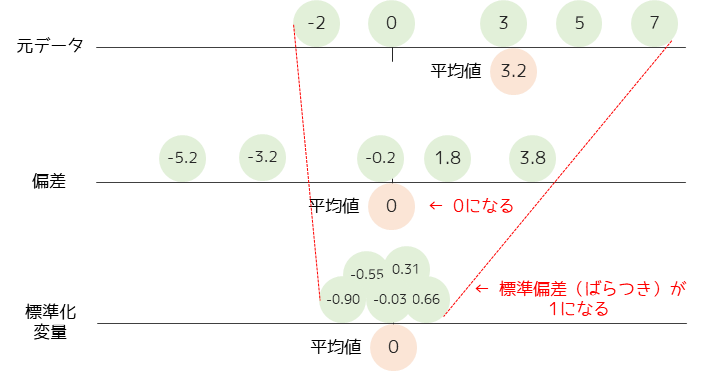
元データから平均値が0になるように変換した値を偏差と言います.標準化変量ではさらに標準偏差を1にするため,データのばらつきが0を中心に小さくなります.
標準化変量ziは以下の式で求めることができます.
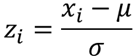
μは平均値,σは標準偏差になります.
標準化変量は単位に影響されないデータ間の比較を行うことができます.例えば,以下のようにある学生のテストの点数があったとします.

得点だけ見ると物理の点数が化学の点数より高いです.各得点の標準化変量を比較すると,化学の方が高いことがわかります.これは,化学のテストの方が他の学生と比較して良い成績であると言うことができます.
Excelを用いた標準化変量の求め方
Excelを用いた標準化・標準化変量の求め方を解説します.
以下のような表を作成して標準化変量を求めます.
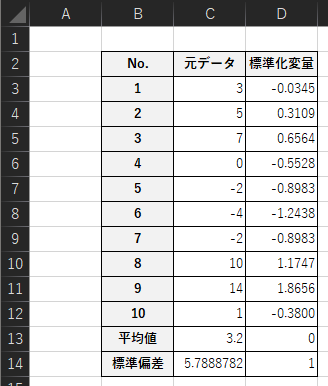
各セルの入力式は以下のようになります.
・C13:=AVERAGE(C3:C12)
・C14:=STDEV.S(C3:C12)
・D3:=(C3-C$13)/C$14
計算手順について説明します.
① 平均値と標準偏差を求める
標準化を行う際に必要な値である平均値と標準偏差を計算します.平均値はAVERAGE関数で,標準偏差はSTDEV.S関数で求めることができます.
② 標準化変量を求める
平均値と標準偏差を用いて,標準化変量を計算します.Excelでは数式をコピーする際に,セルに合わせて参照先が変わってしまうため,上記のように絶対参照($マーク)を使うと簡単に入力できます.
偏差値の関係
日常生活で耳にする偏差値は,標準化変量を用いた値です.偏差値は以下の式で求めることができます.
偏差値 = 50 + 10 × 得点の標準化変量
あるテストの偏差値は,得点の標準化変量を10倍した値に50を加えることで求めることができます.
偏差値は標準化変量の原点を50にずらしているため,50未満であれば平均値より低いことを意味します.また,標準化変量と同様に他の人と比較した自分の得点(良いのか・悪いのか)を知ることができます.









