共分散構造構造分析とは
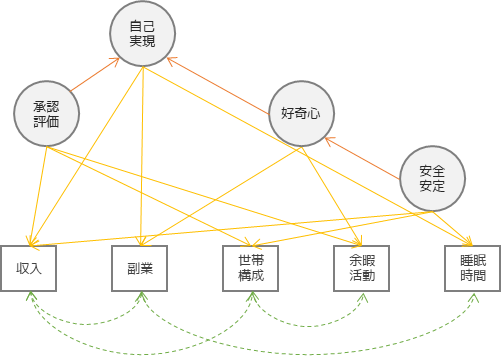
共分散構造分析(CSA;Covariance Structure Analysis)は,因子分析と重回帰分析を組み合わせたような分析手法です.因子分析では共通因子を見つけ出すということが可能でしたが,共分散構造分析では潜在変数(因子)間での関係性(赤矢印)についても調べることができます.
特に心理学の研究や,マーケティング分野でデータの背景にある関係性を調べるために用いられます.
共分散構造分析は基本的には連続変数(数値データ)のみに対して実行可能ですが,カテゴリーデータや時系列データなど,データの種類によって柔軟なモデリングを行う分析手法は構造方程式モデリング(SEM;Structual Equation ModelingSEM)とも呼ばれます.
観測変数間だけの関係性(回帰方程式のみ)について分析はパス解析と呼ばれます.
パス図
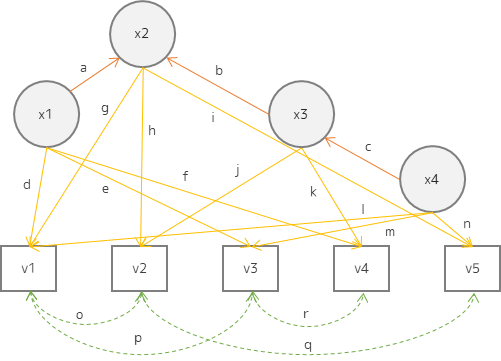
共分散構造分析では,パス図を作成して変数間の関係性を表現します.パス図は以下の要素で構成されます.
観測変数(v1 – v5)
体重や身長や社会的属性,アンケート結果の回答など実際にデータとして収集することができる変数です.パス図では,四角形で表現することが多いです.
潜在変数(x1 – x4)
観測変数によって定義される概念や因子を表す変数です.因子分析のような共通因子と,特定の変数のみに影響を与える独自因子があります.パス図では,円や楕円で表現することが多いです.
パス係数(a – q)
パス係数(パラメータ)は変数間の関係性の強さを表現します.回帰分析における回帰係数,因子分析における因子負荷量のような値です.パス図には,パス係数の統計的な有意差を示すp値も添えられる場合があります.
矢印
変数間の関係性を示します.矢印の向きに因果関係を定義します.例えば,以下の回帰式を定義した場合,矢印の向きは図のように x1 → v1となります.
v1 = d*x1 + e ※ eは誤差
両矢印の場合は,観測変数間の残差相関を表現します.残差相関とはモデルが捉えていない他の要因によって,両方の観測変数に共通の影響が及んでいることを示唆する値です.パス図において,残差相関は点線で繋いだ両矢印で表されることが多いです.
共分散構造分析は観測変数間の関係性を示す残差相関に加えて,測定モデルと構造モデルに分割することができます.
測定モデルは観測変数と潜在変数の因果関係を定義するモデル(図中の黄色矢印),構造モデルは潜在変数間の因果関係を定義するモデル(図中の赤矢印)となります.
モデルの適合度
推定されたモデルが観測データに対して,どれだけ当てはまっているかというのをモデルの適合度と言い,共分散構造分析では様々な評価指標が使用されます.
Χ²検定統計量
帰無仮説を「モデルが正しい」とした場合の検定統計量です.棄却されないことが望ましため,Χ²検定統計量が小さいほどよいです.ただし,サンプルサイズが大きいほどΧ²検定統計量は大きくなるので,あまり意味のない指標となります.
RMESA(Root Mean Square Error of Approximation)
Χ²検定統計量をサンプルサイズ(自由度)で修正した指標値です.目安としては,0.05以下は良好,1以上はあまり良くないとされます.
AGFI(Adjusted Goodness of Fit Index)
重回帰分析の自由度調整済み決定係数に相当する指標値です.目安としては0.9以上が良いとされます.観測変数の数で調整を行わない指標値はGFI(決定係数に相当)と言います.
CFI(Comparative Fit Index)
推定したモデルが全ての変数が無関連である場合のモデルと比較して,どれだけ当てはまりがよいかを示す指標値です.目安としては,0.9以上で許容,0.95以上で当てはまりがよいモデルとされます.
AIC(Akaike Infomation Criteria)
複数のモデルを相対的に評価したい場合に用いる指標値です.目安となる値はありませんが,値が小さいほど当てはまりがよいことを示します.
共分散構造分析の手順
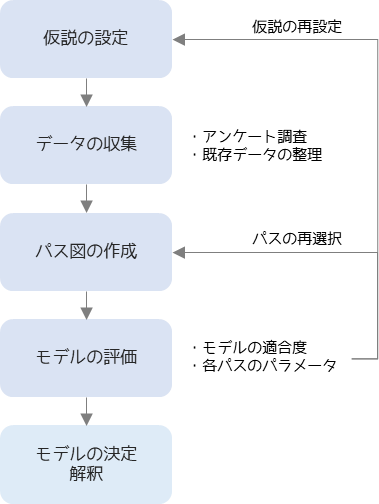
共分散構造分析では,図のような流れで分析を行います.
特に重要なのが仮説の設定です.仮説の設定では分析を行う上で明らかにしたい仮説を立案します.共分散構造分析では様々な因果関係を調べることができますが,分野知識を用いた正しい因果関係の構築を行わないと,誤った結果の算出や解釈をしてしまいます.
具体的には観測変数(収集予定のデータ)に対して,どのような潜在変数(因子)があるかを考え,観測変数←潜在変数や潜在変数↔潜在変数の因果関係を予測します.
パス図の作成では,仮説に則した様々なパターンのパス図を作成して,モデルの適合度やパス係数(パラメータ)を比較します.
最適なモデルを作成できたら,その結果に対して解釈を行います.
共分散構造分析の実行方法
共分散構造分析は複雑な計算が必要なため,専用のソフトやプログラミングが必要です.GUIであれば,SPSSの一部であるAMOS(Analysis of Moment Structures)やStataが有名です.また,R言語ではLavaan(latent variable analysis)というパッケージがよく使用されます.
Staatで販売している統計アプリStaatAppでも,共分散構造分析を簡単に実行することができます.StaatAppを用いた共分散構造分析の実行例や,StaatAppについては以下のページで紹介しています.
》StaatAppで行う共分散構造分析
》統計アプリStaatApp
多母集団同時解析(応用)
共分散構造分析における多母集団(マルチグループ)同時解析は,異なるグループ・属性にわたってモデルのパラメータがどのように異なるか,または一致するかを評価するために使用される高度な手法です.
多母集団同時解析は,文化間での調査の信頼性と妥当性をテストしたり,組織変更が異なる部署にどのように影響するかを理解するために使用されます.また,この手法を用いることで,研究者は理論やモデルが異なるグループにおいて普遍的か,あるいは特定のグループにのみ適用可能かを統計的に検証することができます.










