統計学における尺度
統計学における尺度とは,データが持つ性質の分類になります.
正しい統計解析を行うためは,扱うデータの尺度にあった手法を選択する必要があります.そのためにも,扱うデータの尺度が何かを正しく把握することが重要です.
統計学における尺度は以下の4つになります.
| 尺度水準 | データの種類 | 分類 | 計算 | 統計量 | 具体例 |
| 比例尺度 | 比率データ | 量的データ (数量・連続データ) |
+-×÷ | 平均値,中央値,最頻値 | 身長,金額 |
| 間隔尺度 | 間隔データ | +- | 平均値,中央値,最頻値 | 偏差値,温度 | |
| 順序尺度 | 順位データ | 質的データ | >= | 中央値,最頻値 | 順位,成績(優・良・可) |
| 名義尺度 | カテゴリーデータ | 度数カウント | 最頻値 | 季節(春夏秋冬),職種 |
統計学の尺度は,量的データと質的データに分類することができます.量的データと質的データでは,データの扱い方が大きく異なるため,比例尺度・間隔尺度と順序尺度・名義尺度の違いは特に重要になります.
》質的データの検定手法(ノンパラメトリック検定)
》データの種類別分析手法(多変量解析)
尺度の性質として,上側の尺度ほど情報量が多く上位の尺度になります.上位の尺度では下位の尺度で扱うことができる統計量や,分析手法を適用することができます.
例えば,名義尺度では統計量として最頻値を扱うことができます.比例尺度でも等間隔の度数としてデータを用いることで,最頻値を求めることができます.
間隔尺度で扱うことができる平均値は,順序尺度や名義尺度で算出することはできません.
比例尺度
比例尺度は量的変数で最上位の尺度になります.全ての統計量を算出することができる尺度です.比例尺度における”0”は原点となり,「無」という意味を持ちます.
四則演算や比例変換を行うことが可能で,統計量としては幾何平均や調和平均を算出することができます.
例えば,年収が400万の人に対して年収800万の人は2倍の年収があると言えます.この2倍という値に意味を持つデータが比例尺度です.
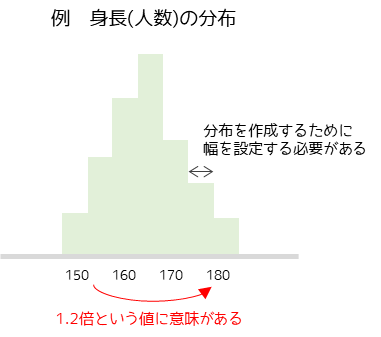
比例尺度の例
身長・金額・人数・時間・年齢・絶対温度
間隔尺度
間隔尺度は,量的変数で値の順序に意味があり,値の間隔が「等間隔」である尺度です.
値の間隔が「等間隔」であるということは,データ間の差に意味を持つ尺度です.例えば,西暦で1995年と2024年は29年の差があると言うことができます.
比例尺度との違いは,比例的な意味を持たないという点です.西暦2000年は西暦1000年に比べて2倍と言うことはできません.
統計量としては,平均や標準偏差を算出することができます.
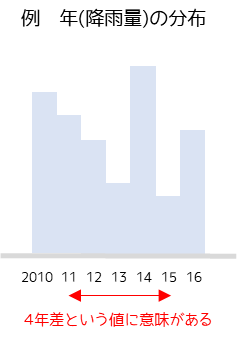
間隔尺度の例
偏差値・温度・西暦
※ 人が予め定義した間隔に沿って示されるデータが間隔尺度に当てはまります.
一定の観測時点ごとに収集されたデータを時系列データと言います.例えば1年ごとの平均降水量や,1日ごとの平均気温は時系列データです.
時系列データは時間の経過がその値に影響を及ぼしている仮定して,過去の値から将来値の予測などを行うことができます.
順序尺度
順序尺度は,質的変数で値の順序に意味がある尺度です.例えば,順位というデータでは1位と2位には明確な順序(大小関係)があります.
間隔尺度との違いは,データ間の差に意味を持たないという点です.1位と2位の差と,3位と4位の差は同じ”1”ですが同じ差であるとは言えません.(テストの順位とした場合,同じ”1”の差でも同じ点数差とは言えません)
統計量としては,中央値や最頻値を算出することができます.平均や分散などを算出することができない点に注意してください.
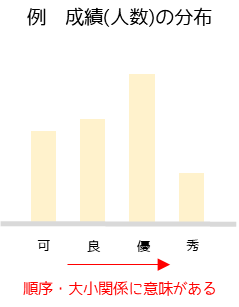
順序尺度の例
順位・成績・段階的評価
順序尺度の1つとして,リッカート尺度という評価尺度があります.リッカート尺度は心理学のような人間を対象とした分析・研究で使用される最も一般的な評価尺度になります.
アンケート調査などでリッカート尺度を用いると,回答結果が順序尺度のデータとして得られるため,ノンパラメトリック検定などの分析が可能となります.
名義尺度
名義尺度は,質的変数で同じ値かどうか以外の意味を持たない尺度です.分類するために,与えられた値であり社会的な属性などが当てはまります.
順序尺度と違い,値の順序に意味を持ちません.例えば性別で男性を0,女性を1とした場合に0と1には大小関係は存在しません.
統計量としては,最頻値を算出することができますが中央値は算出することができません.
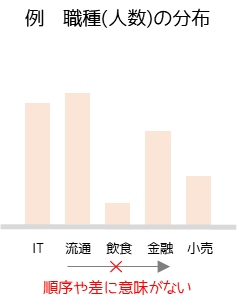
名義尺度の例
性別・季節・職種
分析手法の選び方
扱うデータの種類が判明したら,具体的な分析手法の選択です.統計学における分析手法の選び方は以下のページで紹介しています.









