スピアマンの順位相関係数

スピアマンの順位相関係数とは

スピアマンの順位相関係数とは，2つの変数間の相関の強さを測る指標です．順位データを扱う場合や，2つの変数間に曲線的な関係が想定される場合に用います．

ピアソンの積率相関係数（一般的な相関係数）のノンパラメトリック版になります．

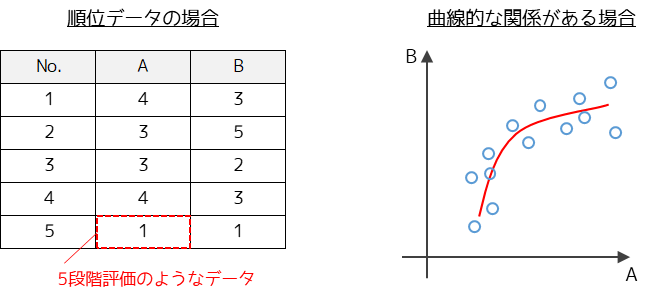
スピアマンの順位相関係数は，-1から1の値を取ります．値の絶対値が大きいほど2つの変数の相関が強いことを表します．

統計学的に相関係数に対する基準はありませんが，目安としては以下のようになります．

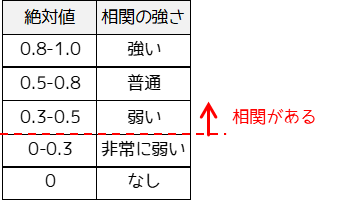
一般的には絶対値が0.3以上ある場合に，2つの変数に相関関係があると判定します．相関係数が0でない（0.1などでも）場合「2つの変数に相関関係がある」と言います．

》相関係数についてさらに詳しく

計算結果を間違えたくない方へ

ExcelやPythonを用いた計算方法より簡単に，スピアマンの順位相関係数・無相関の検定結果を調べることができる統計解析アプリStaatAppを販売しております．

StaatAppではスピアマンの順位相関係数以外にも様々な統計解析をクリックするだけで実行することができます．詳細は以下のページをお読みください．

》統計解析アプリStaatApp
》StaatAppでスピアマンの順位相関係数・無相関の検定を行う

例題の設定

具体的に計算手順を説明するために例題を設定します．

以下のように給料に対する満足度（A）と会社に対する満足度（B）を5段階で評価したデータがあるとします．

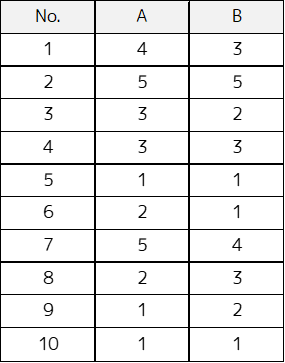
スピアマンの順位相関係数を求めることで，給料に対する満足度と会社に対する満足度の相関関係を調べます．

Excelを用いた計算方法

Excelを用いたスピアマンの順位相関係数の求め方を解説します．

以下のような表を作成して，スピアマンの順位相関係数ρとp値を求めます．

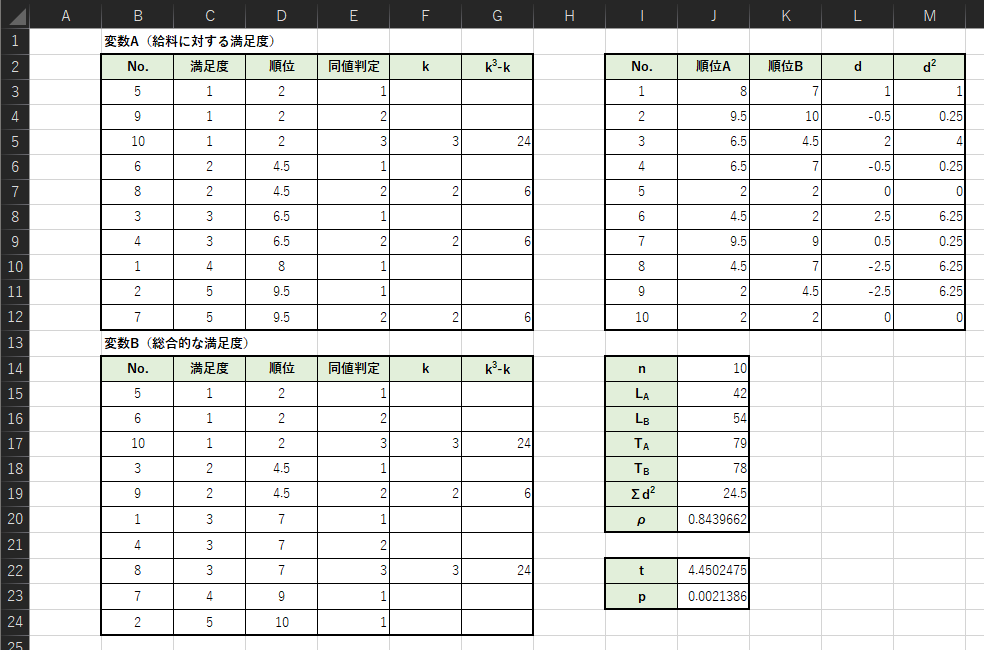
入力式の例は以下になります．　
　・D3：=RANK.AVG(C3,C$3:C$12,1)
　・E3：=IF(C2=C3,E2+1,1)
　・F3：=IF(AND(OR(E4=1,E4=””),NOT(E3=1)),E3,””)
　・G3：=IF(F3=””,””,F3^3-F3)
　・L3：=J3-K3
　・M3：=L3^2
　・J15：=SUM(G3:G12)
　・J16：=SUM(G15:G24)
　・J17：=(J14^3-J14-J15)/12
　・J18：=(J14^3-J14-J16)/12
　・J19：=SUM(M3:M12)
　・J20：=(J17+J18-J19)/(2*SQRT(J17*J18))
　・J22：=J20/(SQRT((1-J20^2)/(J14-2)))
　・J23：=TDIST(J22, J14-2, 2)

計算手順について説明します．2つの変数ごとに同じ値がない場合はタイデータ（同順位データ）の補正は行なう必要はありません．

① データを入力して順位データを求める【B-D列】
　2つの変数ごとにデータを入力します．

　データを入力したら変数ごとに順位データに変換します．ExcelではRANK.AVG関数を用いることで順位データを計算することができます．

　RANK.AVG関数の書き方：=RANK.AVG(“順位に変換する値”,”順位の対象となるデータ範囲”,1)
　※ 値が小さいほど順位が高くなるように計算します．

② 順位データを隣同士の列にコピーする【J3-12】【K3-12】
　順位データの差を求めるために，別のセルに値をコピペします．

③ データを並び替える【B-D列】※タイデータの補正
　順位データの大きさ順（満足度の大きさ順）で並び替えます．

　Excelで値を並び替える際は，並び替え判定を行なう範囲を選択後右クリックをして表示される，「並び替え(O)」機能を用いると周囲の列ごと並び替えることができます．

④ 補正値を求める【E列】【F列】【G列】【J15】【J16】※タイデータの補正
　順位相関係数を求める際に必要な補正値を求めます．補正値は各変数に対して以下の式で求めることができます．

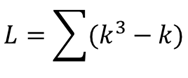
　kはタイデータの個数になります．例題の変数Aには2位が3つあるためk＝3となります．全てのタイデータに対してk³–kを求め，その総和が補正値Lになります．

　補正値L_Aを「J15」セルで，補正値L_Bを「J16」セルで計算するために，「E列」・「F列」・「G列」で必要な値を計算します．

⑤ 補正項を求める【J17】【J18】※タイデータの補正
　補正値から補正項T_A，T_Bを求めます．補正項は以下の式で求めることができます．

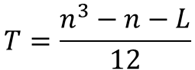
　nはサンプルサイズになります．

⑥ 順位データの差の2乗値を求める【L3-12】【M3-12】
　順位データの差の2乗値を求めます．

⑦ 差の2乗値の合計値を求める【J19】
　差の2乗値の和を求めます．

⑧ 順位相関係数を求める【J20】
　スピアマンの順位相関係数を求めます．順位相関係数ρは以下の式で求めることができます．

　例題ではタイデータがあるため，2つ目の式を用いて計算します．スピアマンの順位相関係数ρ=0.8439..となり，給料に対する満足度と会社に対する満足度は強い相関があると言えます．

⑨ 検定統計量を求める【J22】※ 順位相関係数の検定については補足①で解説します．
　順位相関係数の検定統計量ｔを求めます．検定統計量は以下の式で求めることができます．

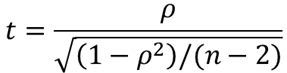
⑩ p値を求める【J23】
　検定統計量からp値を求めます．検定統計量ｔは近似的に自由度n-2のｔ分布に従うため，ExcelではTDIST関数を用いて求めることができます．

　TDIST関数の書き方：=TDIST(“検定統計量”, n-2, 2)

以上がExcelを用いた計算手順になります．

補足① 検定方法とp値について

スピアマンの順位相関係数に対する仮説検定では，求めた相関係数が統計学的に有意であるかを判定します．

帰無仮説は「2つの変数に相関関係はない」となり，有意差がある場合帰無仮説は棄却され対立仮説である「2つの変数に相関関係がある」という結論を得ることできます．

一般的にはサンプルサイズが20以上の場合，Excelの計算方法で解説したｔ分布に従うp値を求め有意差判定を行います．（例題ではサンプルサイズは10ですが説明のため，ｔ分布を用いて検定を行っています）

サンプルサイズが小さい場合は，下記の表の値と順位相関係数を比較することで判定することができます．

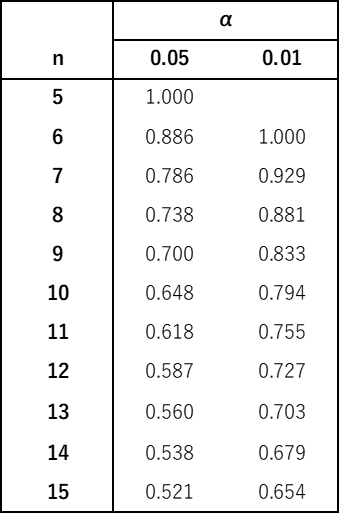
例題では順位相関係数ρ=0.8439..であったので，有意水準α=0.05，サンプルサイズn=10の場合の限界値0.648より大きいため帰無仮説は棄却され「2つの変数に相関関係がある」といった結論を得ることができます．

補足② Pythonを用いた計算方法

Pythonを用いたスピアマンの順位相関係数とp値の計算方法について，サンプルコードは以下になります．

from scipy.stats import spearmanr

salary = [4, 5, 3, 3, 1, 2, 5, 2, 1, 1]
comp = [3, 5, 2, 3, 1, 1, 4, 3, 2, 1]

correlation, pvalue = spearmanr(salary, comp)
print(correlation, pvalue)

==> 実行結果
0.8439661644432728 0.0021385963588282444

PythonではScipyライブラリを用いてp値を計算することができます．

出力結果は順位相関係数が0.843…で，p値は0.00213…となっており，Excelでの計算結果と一致することがわかります．

補足③ ケンドールの順位相関係数との違い

スピアマンの順位相関係数と同様に，ノンパラメトリックな相関係数としてケンドールの順位相関係数があります．

統計学的に使い分ける基準は特にありあせん．ケンドールの順位相関係数と比較してスピアマンの順位相関係数は絶対値が大きくなる傾向があります．

変数内に同順位のデータがある場合はスピアマンの順位相関係数を使うことをおすすめします．Excelの計算的にもスピアマンの順位相関係数の方が簡単です．

》ケンドールの順位相関係数