多変量解析の1つである因子分析について,図と例題を用いて徹底解説しています.
因子分析の手順や結果の見方,主成分分析との違いについても解説しています.
因子分析とは
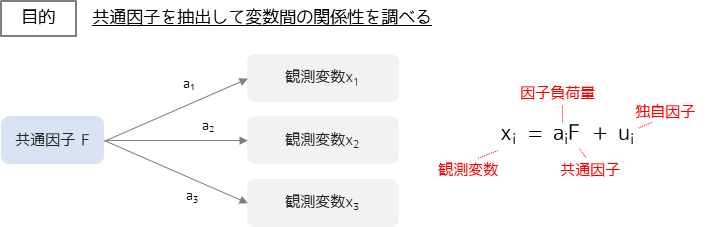
因子分析とは,変数に共通して影響を与えている概念(共通因子)を抽出して変数間の関係性を調べる手法です.
観測変数と因子負荷量,共通因子の関係は図のようになります.観測変数は因子負荷量と共通因子の積に独自因子を加えた値であると定義して,因子負荷量・共通因子を求めます.
因子分析の活用例
因子分析の具体的な活用例を紹介します.
社会人1年目の20人に対してアンケートを取り,回答者には仕事の悩みを5段階(1:当てはまらない-5:当てはまる)で評価してもらいました.
アンケート項目(観測変数)は以下の通りです.
x1:残業が多い
x2:仕事にやりがいを感じない
x3:給料が少ない
x4:休みが少ない,または取りにくい
x5:単純作業が多くスキルアップする見込みがない
x6:業務量が多い
x7:やりたい仕事をさせてもらえない
x8:人間関係がうまくいかない
因子分析の結果,x1,x4,x6に強く影響を与えている共通因子が見つかったとします.

これらの観測変数に共通すること要因として,”労働時間が長い”ということが考えられます.x1,x4,x6のアンケート項目に対して当てはまると回答した人の悩みの根本原因は,労働時間が長いでのはないかと推測することができます.
このように,因子分析を用いることで観測変数に隠れた潜在意識や,根本原因を推測することができます.
因子分析の手順
因子分析は以下の手順で行います.
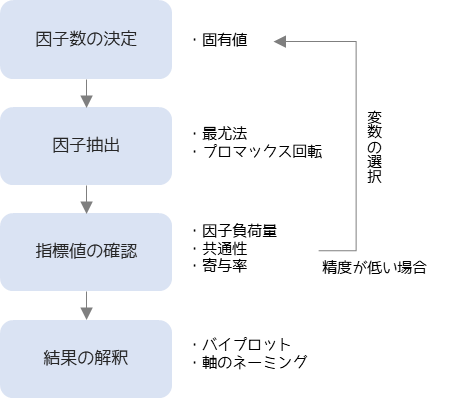
因子分析は分析前に因子数を決めます.因子数を決定する参考値としては固有値(2以上の数)を用います.
因子抽出(分析の実行)では因子数分の因子を抽出します.因子の抽出方法としては一般的に最尤法が,軸の回転方法としてはプロマックス回転が使われます.
分析結果として抽出した因子・観測変数ごとの因子負荷量・共通性・寄与率を確認します.精度が低いと判断した場合は不要な観測変数を取り除いたり,軸の回転方法を変更して再度因子分析を行います.
因子分析の結果の解釈にはバイプロットを用いられます.バイプロットから軸のネーミングを行うことで観測変数に隠れた潜在意識や根本原因を推測を行います.
因子分析の実行方法
因子分析は非常に複雑な計算が必要なため,手計算やExcelを用いて行うことは難しいです.因子分析は一般的にRやPython,有料統計解析ソフトを用いて行われます.
本サイトでは2つの方法を紹介しています.
① Pythonを用いた方法
Pythonを用いた方法に初めてプログラミングを行う方でもわかるように解説しています.
》Pythonを用いた統計解析
》Pythonを用いた因子分析
② 統計解析アプリ(StaatApp)を用いた方法
StaatAppとは任意のデータをマウス操作だけで統計解析ができるPC用アプリです.Rと比較しても簡単かつ正確に分析を行うことができます.
》StaatAppで行う因子分析
》統計解析アプリStaatAppとは
各指標値の意味と解釈
因子分析の実行結果は以下のように出力されます.
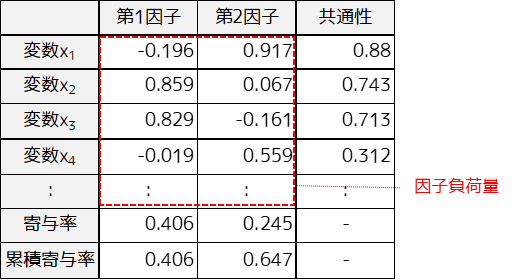
① 因子負荷量
因子負荷量とは各因子と各変数の関連性の大きさになります.各因子に関係性が深い変数ほど絶対値が大きくなり-1から1の間の値を取ります.
x2,x3は第1因子に対する因子負荷量が大きいため,第1因子はx2,x3に強く影響を与えている共通因子であることがわかります.
② 共通性
共通性は各変数の持つ情報が因子モデルにどれだけ反映されているかを示しています.共通性の小さい変数は因子モデルから削除して,再度因子分析を行うとより良い結果を得ることができます.
x4は共通性が比較的低いため,あまり因子モデルに情報が反映されていないと言えます.
③ 寄与率・累積寄与率
寄与率とは,各因子がどれだけの情報を説明できているかという指標になります.
第1因子の寄与率は約40%,第2因子の寄与率は約25%であり累積寄与率は約65%であることが分かります.累積寄与率は60%を超えるとよいとされています.
結果の解釈(軸のネーミング)
因子分析の結果は各因子に名前をつける(軸のネーミング)ことで解釈を行います.各因子との相関の度合いを表す因子負荷量を見ることで因子に名前を付けます.
軸のネーミングにはバイプロットがよく用いられます.バイプロットとは各因子の因子負荷量のベクトル表記と,因子得点をプロットした図になります.
以下の図ように第1因子を横軸に第2因子を縦軸にしたバイプロットを作成したとします.プロット(数字)は因子得点で,2つの因子に対する各サンプル(回答者)の関連性を示します.
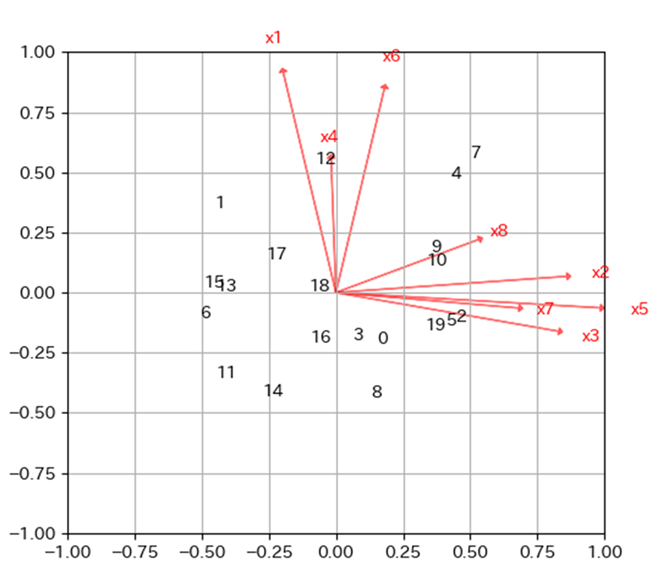
ベクトルの大きさが因子負荷量の大きさを示すので,視覚的に以下のことがわかります.
■第1因子が強く影響している変数
x2:仕事にやりがいを感じない
x3:給料が少ない
x5:単純作業が多くスキルアップする見込みがない
x7:やりたい仕事をさせてもらえない
■第2因子が強く影響している変数
x1:残業が多い
x4:休みが少ない,または取りにくい
x6:業務量が多い
影響を与えている変数の共通点から,第1因子は”仕事に対するやる気が低い”,第2因子は”労働時間が長い”とネーミングすることができます.第1因子と第2因子に名前を付けたことで,アンケート結果の解釈を質問項目以外の観点から行うことができます.
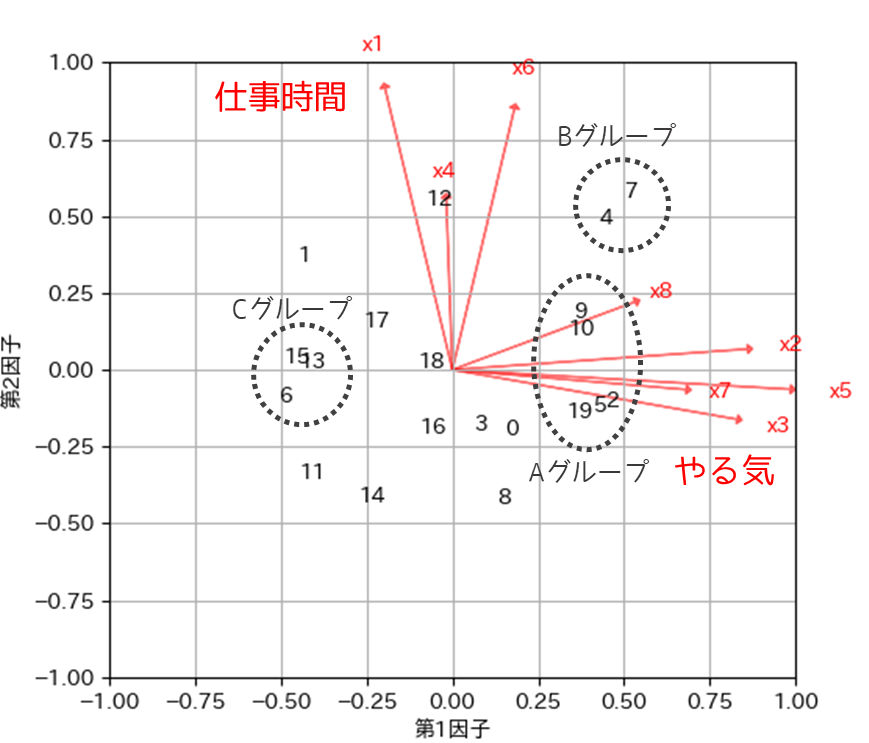
Aグループの位置にプロットされた人は仕事に対するやる気が低く,Cグループの位置にプロットされた人はやる気が比較的高いと解釈することができます.Bグループの位置にプロットされている人は,やる気が低く労働時間も長いと解釈することができます.
補足① 軸の回転
軸の回転とは,変数に対して因子の当てはまりが良くなるように原点を中心に座標軸を回転させることです.共通因子が何を意味しているか分かりづらい場合に軸の回転を行います.
2つの軸がなるべく変数に重なるように回転させることで,変数ごとの因子負荷量が大きくなり因子の特徴を捉えやすくなります.
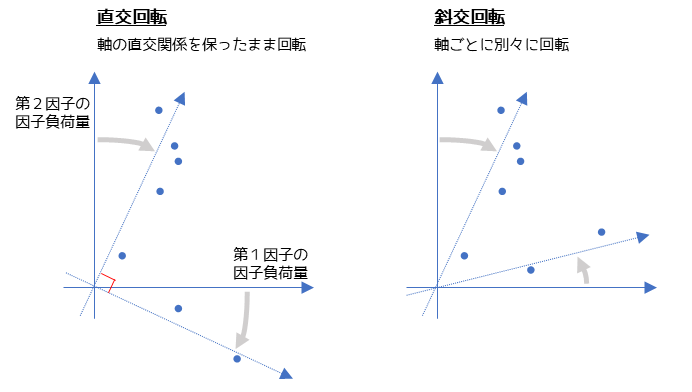
軸の回転基準を設定する方法には,直交回転と斜交回転の2つがあります.直交回転は因子間の相関を仮定しないモデルで,斜交回転は因子間の相関を仮定するモデルになります.データによっては斜交回転を行っても相関がほとんどない場合もあります.
回転基準としてよく使われるのは斜交回転になります.斜交回転の方が柔軟なモデリングを行える分,より単純構造に近づく(因子の特徴が説明しやすくなる)からです.特に例のような,心理学が関わる因子分析でよく用いられます.
斜交回転の中ではプロマックス(promax)回転が論文などでもよく使われます.直交回転ではバリマックス(varimax)回転がよく使われます.
補足② 因子の抽出方法
因子の抽出方法(因子負荷量の計算方法)には,主に以下の3つの方法が用いられます.
| 最尤法 | 多変量正規分布を用いた最尤推定法により因子負荷量を求めます.最も使われる計算方法. |
| 最小残差法 | 残差を最小にするように因子負荷量を求めます.最尤法に近い傾向がある. |
| 主因子法 | 因子の寄与率が最大になるように因子負荷量を算出. |
補足③ 主成分分析との違い
因子分析は主成分分析と類似した分析手法ですが,考え方や目的は大きく異なります.
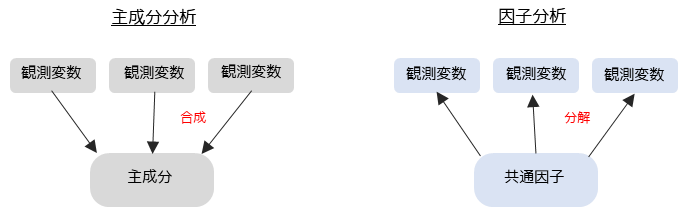
主成分分析は多変量解析の中でも,観測変数を要約するために用います.観測変数の影響を与えている共通因子を調べる因子分析とは,正反対の分析方法になります.









