データ分析・統計解析手法について,目的ごとにどのような方法があるか紹介します.
データ分析・統計解析手法一覧
統計学には様々な解析手法があります.どのような解析手法を行うかは,目的と扱うデータの種類によって決まります.
データ分析の目的と分析手法一覧は以下のようになります.
|
目的
|
統計学的な表現
|
主な分析手法
|
難易度 |
| 要約する | 基本統計量 | 平均値・中央値・分散 | ★ |
| 分布の可視化 | ヒストグラム・箱ひげ図 | ★★ | |
| 多変量解析 | 主成分分析・因子分析 | ★★★★★ | |
| 差を調べる | 仮説検定 | 対応のないt検定・カイ二乗検定・マンホイットニーのU検定 | ★★★ |
| 関連性を調べる | 相関 | ピアソンの積率相関係数・クラメールの連関係数 | ★★ |
| アソシエーション分析 | アソシエーション分析 | ★★★★★ | |
| 因果関係を調べる | 回帰 | 重回帰分析・ロジスティック回帰分析 | ★★★★ |
| 因果推論 | 共分散分析・傾向スコアマッチング | ★★★★★ | |
| 分類する | 教師なし分類 | k-means法・デンドログラム | ★★★★ |
| 教師あり分類 | 決定木・ロジスティック回帰分析 | ★★★★★ | |
| 予測する | 回帰 | 回帰分析・ロジスティック回帰分析 | ★★★★ |
| 時系列分析 | ボックス・ジェンキンス法 | ★★★★ | |
| 機械学習 | 決定木・ランダムフォレスト・サポートベクターマシン | ★★★★★ |
難易度が高いほど,分析を行なうために専用の統計解析ソフトが必要であったり,分析結果を解釈するための学習コストが高くなります.
要約する(基本統計量)
要約する手法である基本統計量は,平均値や中央値などデータの傾向を示す指標になります.
基本統計量はどのようなデータ分析を行う場合でも,必ず最初に計算を行いデータの傾向を把握します.

求めることができる基本統計量は,データの種類によって異なります.例えば,平均値・分散であれば量的データに対してのみ計算することができます.
要約する(分布の可視化)
分布の可視化とはグラフを作成して,データの特徴を把握することです.基本統計量だけではわからなかったデータの特徴を調べることができます.統計解析において,代表的な可視化方法はヒストグラムや散布図になります.
このあと紹介する仮説検定や多変量解析を実施する前に行うのが,統計解析の基本手順となります.
要約する(多変量解析)
要約する手法のうち多変量解析は,複数の項目(変数)を用いてデータの特性を捉える統計的手法になります.
基本統計量では各変数に対して個別で値を計算しますが,多変量解析ではデータ全体で計算を行います.

多変量解析には様々手法がありますが,各変数を統合した新しい指標を作る主成分分析や因子分析などがあります.
多変量解析の各手法については,以下のページで解説しています.
差を調べる(仮説検定)
仮説検定とは標本(データ)を用いて,母集団に統計学的に差があるかを判断する方法です.判断の基準としては確率的な表現を用います.
条件が違う実験データや,標本の属性の違いによる差(効果)があるか判定するために行います.仮説検定で1つの変数に対して複数の標本に分けて比較を行います.

比較する際に用いる統計量の種類や標本数によって様々な検定方法があります.
比較対象の変数がカテゴリデータ(性別)の場合は,クロス集計表を作成して分析を行います.
関連性を調べる(相関)
変数間の関連性を統計学では相関と言い,相関係数を求めることで関連性を調べることができます.

相関係数にも様々な種類があり,一般的に相関係数と言われるのは図のように量的データと量的データの関連性を調べる際に計算する,ピアソンの積率相関係数になります.その他の相関係数については,以下のページで紹介しています.
関連性を調べる(アソシエーション分析)
アソシエーション分析は,大量のデータの中からアイテム間の関連性を見つけるための,データマイニングの技術です.
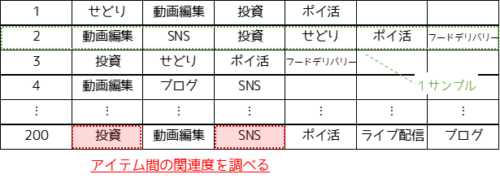
アソシエーション分析では1つのサンプルから同時に含まるアイテムを抽出し,様々な指標値を用いてアイテム間の関連度に意味をもたせます.アソシエーション分析で用いる様々な指標値を,アソシエーションルールと言い”支持度”や,”信頼度”がよく用いられます.
アンケート結果の分析や購入データの分析によく用いられます.
因果関係を調べる(回帰)
因果関係を調べる手法である回帰分析では,変数Aが変数Bに与える影響を調べることができます.
関連性を調べる相関係数と類似していますが,相関係数では因果関係を調べることはできません.
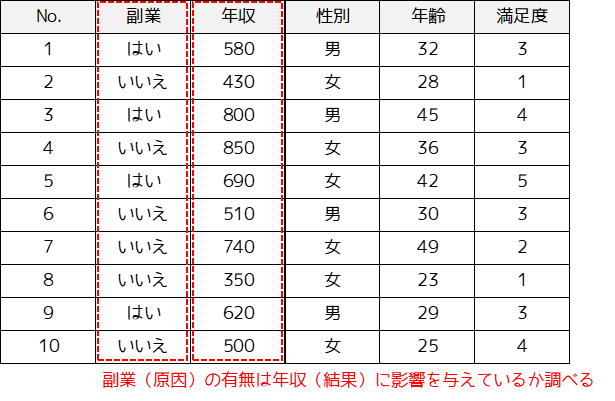
回帰分析では2つの変数の因果関係だけでなく,1つの変数(目的変数)に対する複数の変数(説明変数)の影響度を調べる重回帰分析などがあります.
重回帰分析は3つ以上の変数に対して行う分析手法であり,多変量解析の1つになります.
因果関係を調べる(因果推論)
回帰分析より更に深い分析で因果関係を調べる方法が因果推論です.因果関係を調べる際に重要なのが,調べたい原因以外の要因による影響です.正確な分析を行うために調べたい原因以外の要因は,なるべく取り除く必要があります.
観測データから調べたい結果と原因に影響を与える要因(交絡因子)を,取り除く手法が因果推論になります.

因果推論では年収(結果)に与える副業(原因)の影響を調べる際に,年収に影響を与えている年齢(交絡因子)を取り除くことができます.
分類する(教師なし分類)
教師なし分類とは,教師データつまり分類結果の正解を示すデータを含めないで分類を行なうことです.以下のようなデータであれば,社会人の属性の関するデータから分類手法の規準に従って,似ているデータ(社会人)ごとに分類されます.

教師なし分類の具体的な手法としては,k-means法やデンドログラム(樹形図)があります.これらの手法を総称して,クラスター分析と表現することも多いです.
学習用のデータを用意する必要がないので,教師あり分類と比較してより簡単に行える手法です.教師なし分類と教師あり分類については機械学習のページでより詳細に解説しています.
分類する(教師あり分類)
教師あり分類では,予め教師データつまり分類結果の正解を示したデータを用いて学習を行います.学習した結果と分類したいデータ(ラベルがないデータ)を用いて分類を行います.

教師あり分類の手法としては,決定木やロジスティック回帰分析,判別分析などがあります.
予測する(回帰)
回帰分析では因果関係を調べることに加えて,予測式を求めることができます.
求めた予測式に説明変数を代入することで,目的変数の値や確率を計算することができます.

上記のように目的変数(副業の有無)が2値データの場合,ロジスティック回帰分析を行います.
予測する(時系列分析)
時系列データ(一定の間隔ごとに観測したデータ)に対しては,時系列分析を行うことで将来の値を予測することができます.
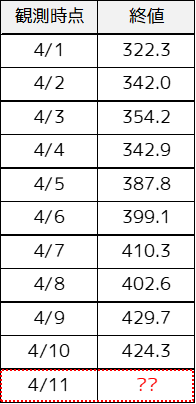
例えば,過去の終値(株価)のデータから時系列モデルを用いることで,将来の値を予測することができます.代表的な手法としてはボックス・ジェンキンス法などがあります.
予測する(機械学習)
機械学習は統計モデルを用いないという点では統計解析とは異なりますが,多変量解析と同様に複数の変数から個体を分類したり,学習結果から未知のデータを予測することができます.

分類・予測する手法としては,決定木という分析手法がよく使用され,機械学習の中では比較的に簡単に扱うことができます.
補足① データの入力・加工方法
データ分析を行うためには,正しくデータを入力・加工する必要があります.
既にデータがある方も,これからデータを作成・収集する方も以下のページで確認してみてください.
補足② Excelで行う統計解析
本ページで紹介した統計解析手法を,Excelで行う方法を本サイトでは解説しています.
以下のページで一覧にして紹介しているので,実際に計算を行いたい方は参考にしてください.
データ分析を行うならStaatApp
データ分析を本格的に行う場合,RやPythonを用いたプログラミングもしくは統計解析ソフトが必須となります.
統計解析アプリStaatAppではマウス操作だけで,簡単・正確に統計解析を行うことができます.本ページで紹介した手法も全て対応しており,分布図の作成や時系列分析,決定木については無料で実行できるので,気軽にダウンロードしてお使いください.










