時系列分析で一般的に使われるボックス・ジェンキンス法について,実践例を用いて解説します.
実践例で使用している統計解析アプリStaatAppはこちらのページから無料でダウンロードできます.
ボックス・ジェンキンス法とは
ボックス・ジェンキンス法とは,時系列データの分析と予測を行うための手法です.これは統計学者のジョージ・ボックスとグウィリム・ジェンキンスによって開発されました.時系列データの特徴を把握して,適切なモデルを作成し最終的には将来予測を行うことを目的とした手法です.
ボックス・ジェンキンス法は以下のような手順で行います.
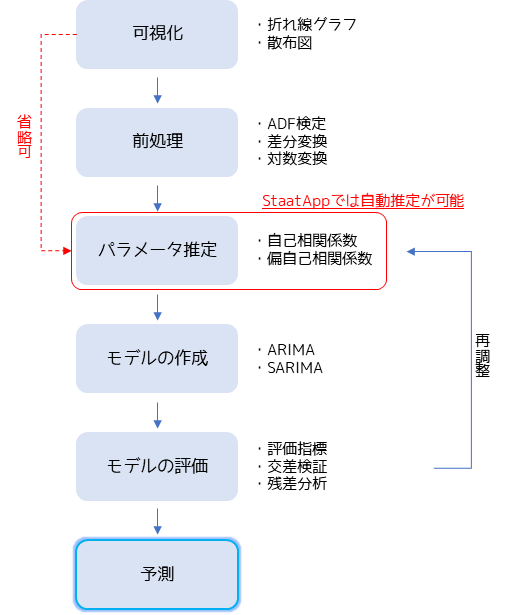
時系列データの特徴を把握するために,折れ線グラフや散布図を用いて可視化を行います.作成したグラフから時系列データの長期変動や季節変動の有無を調べます.
グラフから時系列データが非定常過程であると判断した場合はデータの前処理として,差分変換・対数変換を行います.定常性過程のADF検定を用いて判定することも可能です.ボックス・ジェンキンス法で主に用いるモデルであるARIMAやSARIMAでは長期変動や季節変動を考慮することができるため,非定常過程の時系列データのまま手順を次に進めても問題ありません.
パラメータ推定では時系列データの自己相関係数や偏自己相関を求めることで,モデル作成に必要な値を算出します.パラメータ推定では時系列データが非定常過程である場合,推定するパラメータが多くなるため推定するパラメータを少なくしたい場合は先程の前処理で定常性過程に変換する必要があります.ただし,StaatAppではパラメータ推定を自動で行うことが可能です.
推定したパラメータを用いてモデルを作成します.基本的には季節変動がない場合はARIMAモデル,季節変動がある場合はSARIMAモデルを用います.
作成したモデルの評価を行うためには,情報量基準などの評価指標や残差分析を行うことでモデルの精度を評価します.モデルの精度が良くない場合はパラメータを調整を行い,再度モデル構築を行います.
最終的には作成したモデルから将来の予測値を算出することで,時系列データの将来予測を行います.
ARIMAモデルとは
ボックス・ジェンキンス法で用いるARIMA(Autoregressive integrated moving average model,自己回帰和分移動平均モデル)モデルとは,自己回帰モデルと移動平均モデルを組み合わせた時系列分析のモデルです.過去のデータが未来のデータに影響を与えるという考え方に基づいています.ARIMAモデルは長期変動を含む時系列データ(非定常過程)にも適用できます.ARIMAモデルでは差分をとることで,長期変動を除去し定常過程に変換します.
ARIMAモデルは古典的な自己回帰モデルの一種ですが,機械学習やディープラーニングが得意としない小さなデータセットに対しても性能が良いため,様々な時系列データに対して現在でも多く使用されます.
StaatAppを用いたボックス・ジェンキンス法
統計解析アプリStaatAppを用いて,具体的にボックス・ジェンキンス法について解説します.サンプルデータとして,名古屋市の月別平均気温データを用いています.
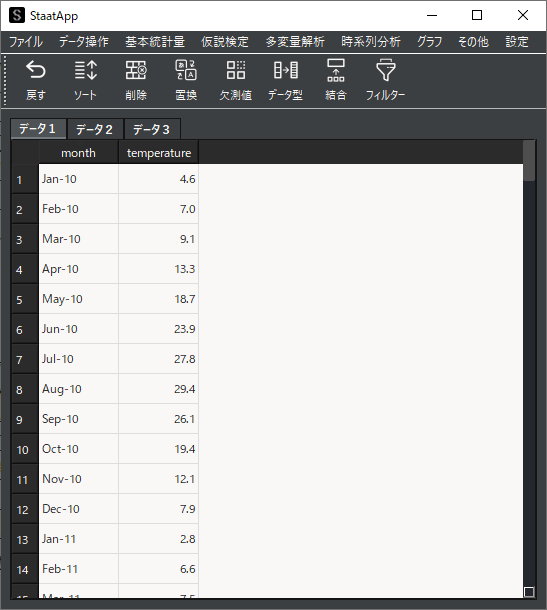
① データの可視化
折れ線グラフ機能を用いて,サンプルデータの可視化を行います.折れ線グラフから長期変動はなく季節変動があるデータということがわかります.
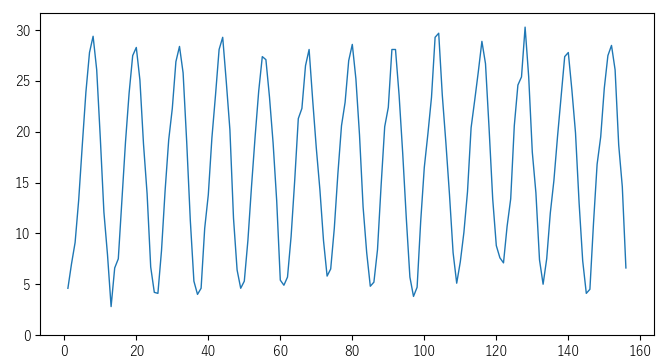
② パラメータ推定
自己相関係数を求めることで季節変動の周期を算出します.自己相関係数機能で以下のようなコレログラムを作成して視覚的に周期を把握します.
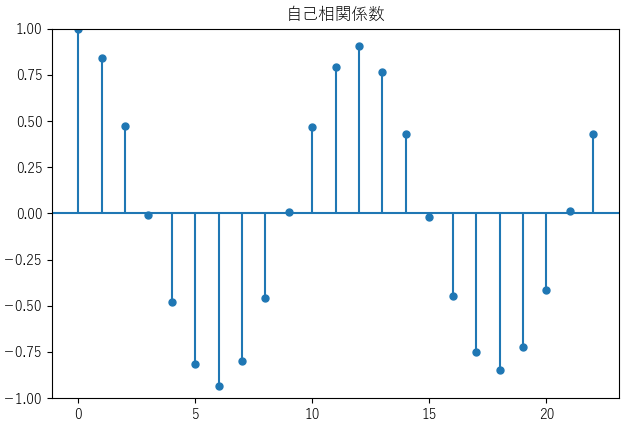
自己相関係数がラグ12の時点で高くなっているため,周期は12と判断することができます.(月別平均気温という特性から当然ですが,,)
③ モデルの作成
ARIMA機能を用いて,ARIMAモデルの作成を行います.
変数選択で対象のデータ列名を選択します.次に季節成分では「季節成分を考慮」を選択して,周期を12に設定します.ARIMA機能では「季節成分を考慮」を選択するとSARIMAモデルが選択されます.
パラメータは自動設定(デフォルト)のままとします.
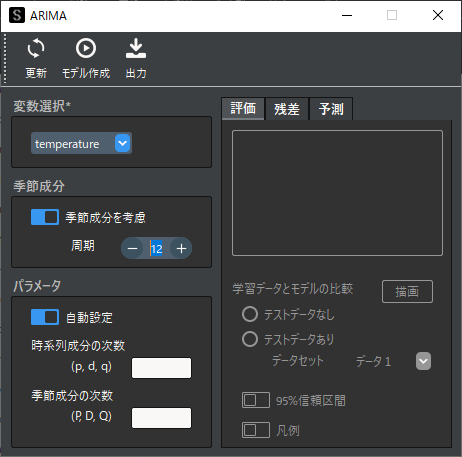
「モデル作成」ボタンをクリックするとモデルが作成され評価指標が表示されます.
④ モデルの評価
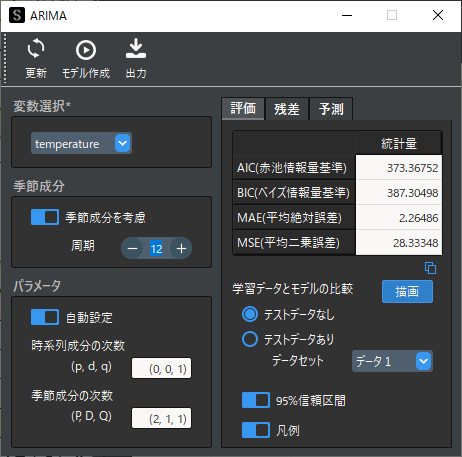
評価指標を用いてモデルの評価を行います.ARIMA機能で算出される評価指標は全て絶対的な基準はありません.各指標とも値が小さいほど,良いモデルであると考えることができます.
StaatAppではモデル作成時のパラメータ自動計算において,AICが最小になるような値を求めて設定しています.
次に残差分析を行います.残差タブの「コレログラム」選択して残差の偏自己相関係数のコレログラムを作成します.
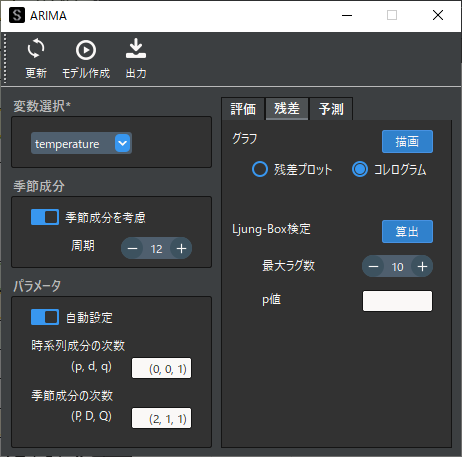
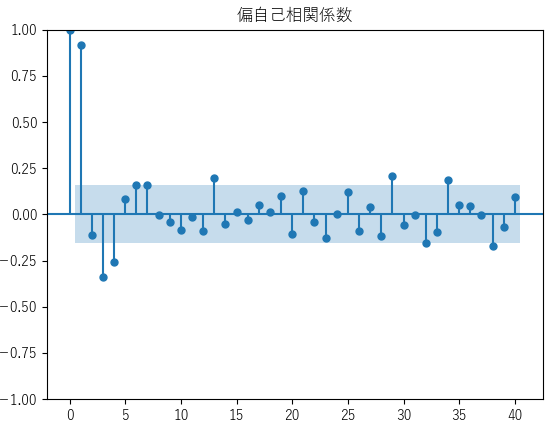
青帯の範囲の外にある値は,有意水準α=0.05で無相関の検定における有意を示します.ラグ5以下の値を除いて,周期ごとに偏自己相関係数が有意となっていますがそれほど大きな値ではないため比較的あてはまりのよいモデルと評価することができます.
⑤ 将来予測
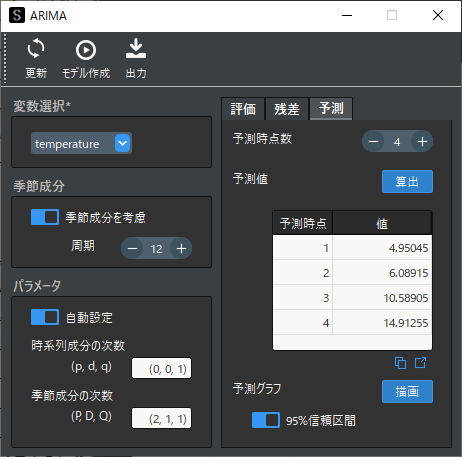
作成したモデルから将来予測を行います.予測タブから任意の時点数の選択して,将来予測を行います.
補足① ホールドアウト検証
StaatAppではモデル評価の方法として,事前に学習データとテストデータを分割して,学習データから作成したモデルの予測値とテストデータを比較するホールドアウト検証が可能です.
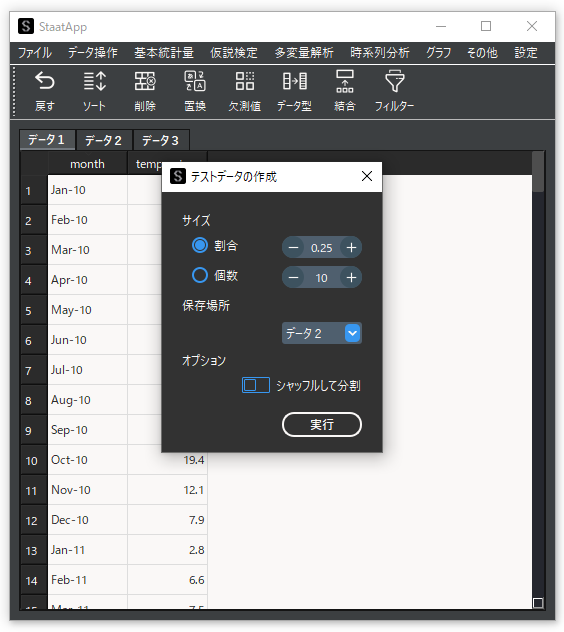
ARIMA機能を用いる前に,読み込ませたデータを「テストデータの作成」機能で分割を行います.テストデータ作成機能ではアクティブデータセットの選択した行数分が分割されて,指定されたデータセットに出力されます.
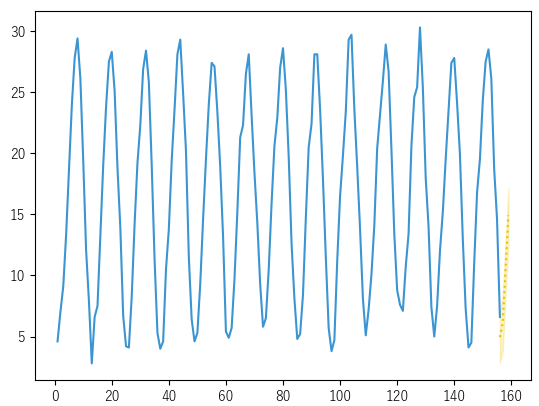
分割を行ったら学習データでモデルを作成して,モデルの評価タブにある「学習データとモデルの比較」で「テストデータあり」を選択すると以下のようなグラフを作成することができます.
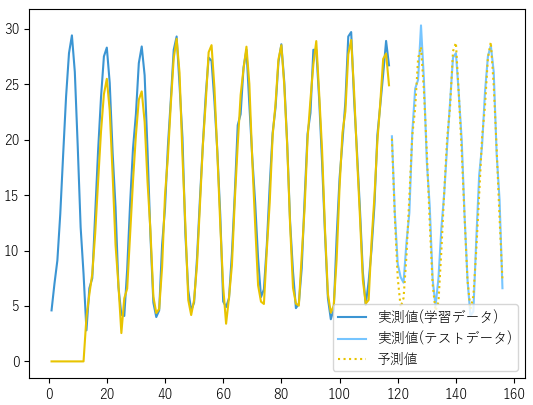
サンプルデータではテストデータと予測値がほぼ一致しているので,当てはまりのよいモデルを作成できたと判断することができます.
補足② ARモデル・MAモデル
ARIMA機能ではデフォルトでパラメータが自動設定されますが,自動設定を行わず任意のパラメータを設定することでARモデルやMAモデルを用いることが可能です.
例えば,AR(1)モデルを用いる場合はパラメータ設定の「時系列成分の次数」に(1, 0, 0)と入力してください.
MA(1)モデルを用いる場合は,(0, 0, 1)と入力します.
補足③ ARIMA機能の詳細仕様
StaatAppのARIMA機能ではPythonの以下のライブラリを使用して演算を行っています.詳細なアルゴリズムや信頼性を知りたい方は公式ドキュメントをお読みください.
・パラメータの自動計算(pmdarima)
・モデルの作成・評価・予測(statsmodels)










