クロス集計表とは
クロス集計表とはアンケート調査などから得られたカテゴリーデータ(名義尺度)に対して,2つの項目(変数)で同時に集計した表のことです.
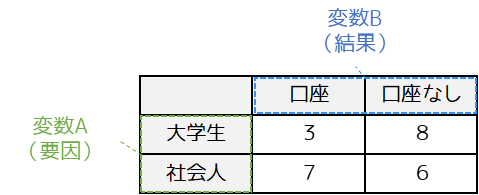
例として,大学生と社会人に対して仮想通貨の取引口座の有無について調査したとします.回答結果から回答者の属性と,口座有無という2つの変数に対してクロス集計を行なうと以下のようになります.
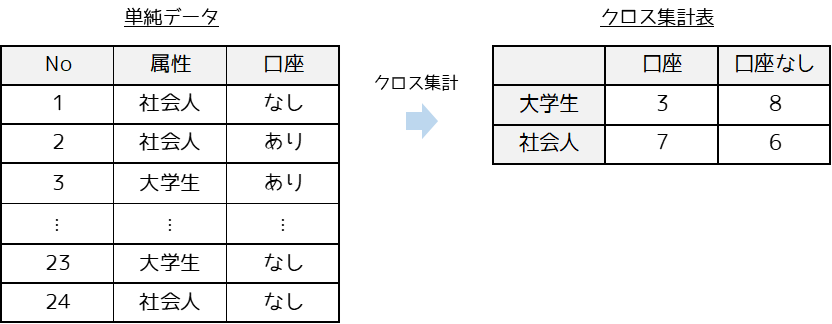
クロス集計表を作成することで2つの変数による影響がわかりやすくなります.上記のクロス集計表を見ることで,「社会人と比較して大学生の方が,取引口座を開設していない傾向がある」といったことがわかります.
クロス集計表を用いる際の注意点としては,集計する変数は順序尺度もしくは名義尺度である必要があります.
》クロス集計とは(さらに詳しく)
》統計学におけるデータの種類
変数間の関係性を調べる
クロス集計を作成した際の分析方法としてよく使う手法が,変数間に関係性があるかを調べるという手法です.
クロス集計表を作成するだけでは,「大学生だから社会人と比較して取引口座を開設していない傾向がある」ということが,感覚的・定性的にしか判断することができません.
統計学的に判断するために,変数間の関係性を定量的に調べる必要があります.
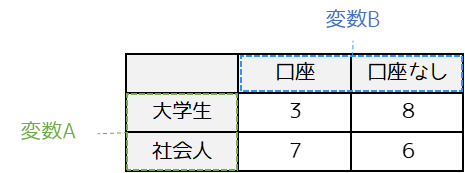
変数間の関係性とは回答者の属性を変数A,取引口座の有無を変数Bとすると「変数Bに対して変数Aは(or 変数Aは変数Bに対して)影響を与えているか」という意味になります.
統計学的には,独立性とも言います.(関係性がない=各変数が独立している)
独立性を判断する手法としては,独立性の検定(カイ二乗検定)とフィッシャーの正確確率検定の2つがよく用いられます.
2つ手法の選び方は,総度数または期待度数の大きさで判断します.クロス集計表で集計した各セルの値の合計値が20以上かつ,各セルの期待度数が全て5以上場合はカイ二乗検定を行います.条件を満たさない場合は小標本とみなしてフィッシャーの正確確率検定を行います.
変数間の関係性を調べる手法として,クラメールの連関係数を調べる方法もあります.クラメールの連関係数は,変数間の関係性の強さを0~1の値で求めることができます.
独立性の検定ではサンプルサイズが大きくなるほど,変数間に関係性がある(有意差がある)と判定しやすくなるため,クラメールの連関係数は純粋に変数間の関係性の強さを調べるために有効です.
影響要因を調べる
クロス集計表は一般的に,上側(表頭)に結果・左側(表側)に要因として作成します.
影響要因を調べるとは表頭に対して,表側がどれだけ影響しているかを調べることを意味しています.(変数間の関係性を調べる手法では,要因と結果を考えません)
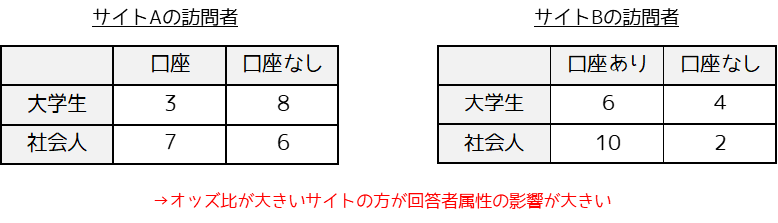
クロス集計表の要因と結果の関係は,オッズ比を用いることで調べることができます.
複数のクロス集計表からオッズ比を求めて比較することで,変数間(クロス集計表間)での影響要因の差を調べることができます.
例題で用いているクロス集計表を2×2のクロス集計表と言いますが,集めたデータによっては2×3のようなクロス集計表ができる場合もあります.2×2のクロス集計表以外の場合でオッズ比を求める際は「対数線型分析」という手法を用います.
視覚的に調べる
クロス集計表の変数内の項目数が多く,集計結果が分かりづらい場合に散布図を用いて見やすくする分析手法があります.
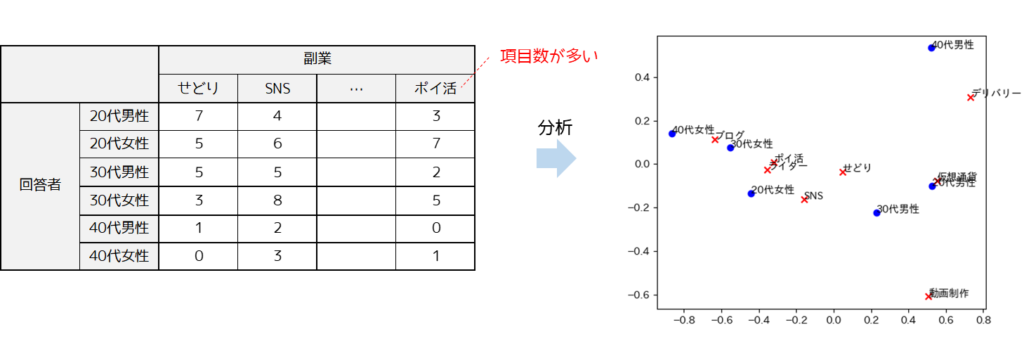
散布図を作成することで変数内の各項目間の関係性を,プロットされた位置で判断することができます.例では仮想通貨と20代男性の関係性が強いと判断することができます.
クロス集計表の結果を散布図にする手法をコレスポンデンス分析と言います.
複数の集計項目,複数のクロス集計に対して分析を行う場合は,数量化Ⅲ類・多重コレスポンデンス分析という手法があります.
クロス集計を用いた分析を行うならStaatApp
Staatではクロス集計表の作成・分析をすることができる統計解析アプリStaatAppを販売しております.
StaatAppではクロス集計表の分析以外にも様々な仮説検定などの統計解析をクリックするだけで実行することができます.詳細は以下のページをお読みください.
》StaatAppで行うクロス集計表の分析
》統計解析アプリStaatApp
補足② ノンパラメトリック検定との関係
クロス集計表の分析のうち独立性の検定は,ノンパラメトリック検定の1つになります.
独立性の検定はノンパラメトリック検定の中でもカテゴリーデータに対しての分析手法です.カテゴリーデータ以外の順位データや間隔データの分析を行なう場合は,マンホイットニーU検定などを行います.
》統計学におけるデータの種類
》ノンパラメトリック検定の選び方