StaatAppにメタアナリシスを実装，解説ページを公開しました！
Python

【Pythonで行う】ロジスティック回帰分析

  /

Pythonのstatsmodelsを用いたロジスティック回帰分析について，初めてPythonを使う方でも分かるように例題を用いて解説します．

ロジスティック回帰のデータの作成方法から結果の解釈の仕方まで解説しています．

プログラミング不要ですぐに実行できるロジスティック回帰分析アプリについてはこちら．

例題の設定

ロジスティック回帰を用いた統計解析を説明するために，以下の例題・データを用います．

「社会人21人に対して，副業の有無・収入・性別・年齢・結婚有無についてのデータを収集しました．収集したデータを用いて副業の有無に影響を与えてる要因について分析を行います．」

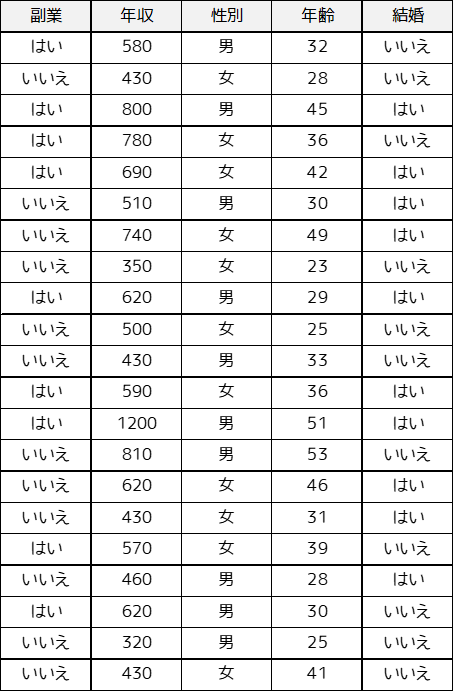
ロジスティック回帰分析用の例題用データ

Pythonで読み込むせるデータ形式（CSVファイル）の作り方はこちら．

プログラムの作成・実行

Pythonを用いてプログラムの作成をします．

➔ 実行環境の作り方（プログラムを記述するまでの手順）

ロジスティック回帰に必要な記述例は以下になります．

# ライブラリのインポート
import pandas as pd
import statsmodels.formula.api as smf
import statsmodels.api as sm

# データの読み込み
workers = pd.read_csv("sample.csv")

# ロジスティック回帰モデルの推定
logistic = smf.glm(formula = "side_job ~ income + sex + age + married",
                   data = workers,
                   family = sm.families.Binomial()).fit()

# 推定結果の出力
print(logistic.summary())

それぞれの記述内容について解説します．

① ライブラリのインポート

ロジスティック回帰で用いるライブラリをインポートします．
3つのライブラリをインポートしますが，記述例と全く同じ内容で問題ありません．

# ライブラリのインポート
import pandas as pd
import statsmodels.formula.api as smf
import statsmodels.api as sm

② データの読み込み

pd.read_csv関数を用いてCSVファイルの読み込み，データフレームに格納します．
データフレーム名（＝の左側）は任意の値を入力します．””内は読み込むCSVファイル名を記述します．

# データの読み込み
workers = pd.read_csv("sample.csv")

③ ロジスティック回帰モデルの推定

statsmodelsを用いてロジスティック回帰モデルの推定を行います．statsmodelsのglm関数は一般化線形モデルの推定に用いる関数です．ロジスティック回帰モデルは一般化線形モデルの1つになります．

　【引数の書き方】
　「formula」：”目的変数 ~ 説明変数１ + 説明変数２ + 説明変数３”形式でロジスティック回帰の目的変数と説明変数の項目名(1行目)を記述します．
　 「data」：データの読み込みで定義したデータフレーム名を記述します．
　 「familiy」：確率分布を記述します．今回は二項分布なので「sm.families.Binomial()).fit()」となります．

# ロジスティック回帰モデルの推定
logistic = smf.glm(formula = "side_job ~ income + sex + age + married",
                   data = workers,
                   family = sm.families.Binomial()).fit()

④ 推定結果の出力

推定結果を出力します．print関数を用いてコンソール上に出力します．

# 推定結果の出力
print(logistic.summary())

以上がstatsmodelsを用いたロジスティック回帰分析になります．

PyCharmを用いている方は右上の「▶」ボタンを押すとプログラムが実行されます．

結果の見方

Pythonでロジスティック回帰を実行すると以下のような結果が出力されます．

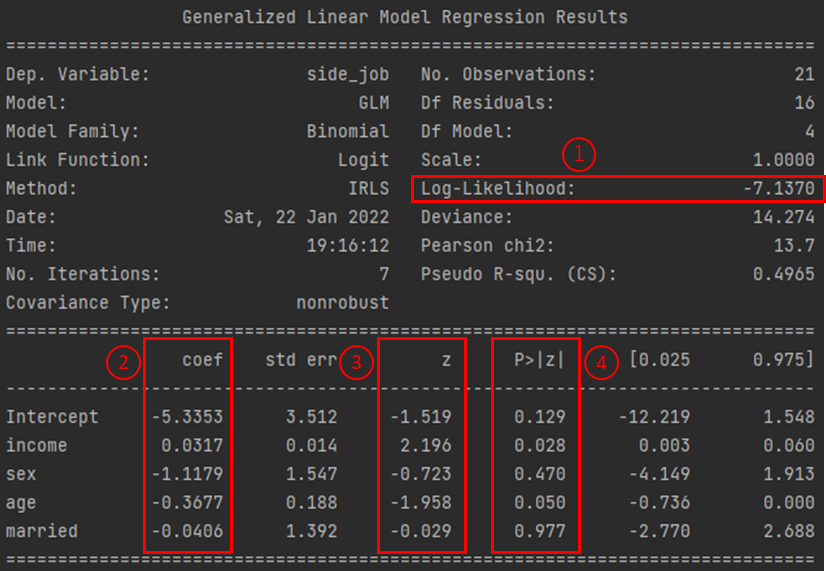
ロジスティック分析の実行結果

ロジスティック回帰分析の結果で見るべきポイントは4つになります．

① 対数尤度

「Log-Likelihood」は対数尤度になります．尤度（ゆうど）とは尤（もっと）もらしさを示す指標になります．対数尤度は値が大きいほど推定した回帰モデルの当てはまり良いことを意味します．

今回のような説明変数の組み合わせが1つの場合は見る必要はありません．説明変数の候補となるデータが他にもあり複数パターンで回帰モデルを推定した際に，対数尤度が最も大きい組み合わせが最も良い回帰モデルであると言えます．

② 偏回帰係数

「coef」は偏回帰係数になります．偏回帰係数は0の場合は，その説明変数は推定した回帰モデルに影響を与えないということを意味します．値が正の場合は確率を上げる方向に，負の場合は確率を下げる方向に影響を与えます．

収入(income)という説明変数は正の値であるため，収入が多いほど副業をしている確率が上がることを意味します．年齢(age)は負の値であるので年齢が上がるほど副業をしている確率が下がることを意味します．

※「Intercept」は回帰モデルの定数項になります．

③ Wald統計量

「ｚ」はWald統計量になります．Wald統計量の絶対値が大きいほど，目的変数に影響を与えているということを意味します．

Wald統計量の絶対値が最も大きいのは収入(income) であるので，副業の有無に最も影響を与えていると言えます．

④ ｐ値

「P>|z|」は偏回帰係数のWald統計量についてのp値になります．p値が有意水準を下回ればその説明変数は有意な偏回帰係数であることが言えます．統計学では一般的に有意水準α＝0.05とすることが多いです．有意水準α＝0.05とは，実際に関連性がない場合でも関連性が存在すると結論付けるリスクが5％であることを意味します．

有意水準α＝0.05とすると，収入(income)のみが統計的に有意であり目的変数に関連性があると言えます．

補足① ロジスティック回帰分析とは

ロジスティック回帰分析とは，複数の要因（説明変数）から結果（目的変数）が起きる確率を説明・予測する統計的手法になります．

ロジスティック回帰分析と似た手法として，重回帰分析があります．重回帰分析との違いは目的変数になります．ロジスティック回帰分析では目的変数が”Yes/No”のような2つの値しか取らない場合に用いることができます．

目的変数が量的変数である場合は，重回帰分析を行います．

》Excelで行なう重回帰分析

その他の多変量解析については，以下のページで詳しく解説しています．

》多変量解析とは？選び方まで解説

補足② 予測値の求め方

回帰モデルとして推定される式と，回帰モデルを用いた予測値の求め方について説明します．

例題で推定した回帰モデルは以下の式になります．

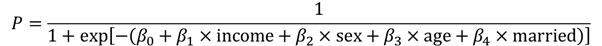
ロジスティック回帰分析の予測式

β0は定数項の偏回帰係数，β1～β4は各偏回帰係数が入ります．

予測値については回帰モデルに値を代入することで求めることができます．ここではPythonを用いた予測値の求め方について紹介します．

以下のような社会人2人がいた場合の副業を行っている確率について予測を行います．

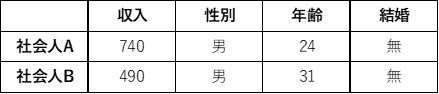
ロジスティック回帰分析の予測結果

statsmodelsを用いた記述例は以下になります．’プログラムの作成’で推定した回帰モデルを用いるので，’プログラムの作成’での記述内容の下に記述してください．

# データの入力
dict1 = dict(income=[740, 490],
             sex=[1, 1],
             age=[24, 31],
             married=[0, 0])
ide_worker = pd.DataFrame(data=dict1)

# 予測値の出力
pred = logistic.predict(ide_worker)
print(pred)

predict関数を用いることで予測値を求めることができます．出力結果は以下になります．

0    0.999712
1    0.088176
dtype: float64

上記の結果から，社会人Aが副業をしている確率は99.9%（高過ぎますね，，）で社会人Bが副業している確率は8.8%であることが分かります．

補足③ 調整オッズ比の求め方

ロジスティック回帰分析の結果からオッズ比を求めることができます．ロジスティック回帰分析の係数から得られるオッズ比を，他の説明変数に依存しないオッズ比として調整オッズ比とも言います．

》オッズ比とは

オッズ比は偏回帰係数の指数関数になるので，以下の記述で求めることができます．

# SciPyのインポート
import scipy as sp

# オッズ比の計算・出力
print('income_odds-ratio:', sp.exp(logistic.params["income"]))
print('sex_odds-ratio:', sp.exp(logistic.params["sex"]))
print('age_odds-ratio:', sp.exp(logistic.params["age"]))
print('married_odds-ratio:', sp.exp(logistic.params["married"]))

出力結果は以下のようになります．

income_odds-ratio: 1.0321695773504087
sex_odds-ratio: 0.3269611884070154
age_odds-ratio: 0.6923468928272201
married_odds-ratio: 0.9602472075989745

オッズ比は質的変数に対してのみ有効な値です．今回の説明変数は性別と結婚有無が質的変数になります．

性別と結婚有無のオッズ比を比較して，結婚有無のオッズ比が大きいため副業への影響が大きいと解釈することができます．（ただし，p値で説明したように2つの説明変数は統計的に有意ではありません．）

補足④ PyCharmを用いた実行環境の構築

Pythonを初めて使う方や，自分のPCにPython・PyCharmが入っていない方は以下のページで解説している手順で実行環境の構築を行ってください．

初めて触る方にもわかりやすいようにPyCharmを用いた手順となっています．ロジスティック回帰で使用するライブラリのインストール方法についても紹介しています．

》Pythonを用いた統計解析【初心者向け】

》実行環境の構築方法【Pycharm使用】
》ライブラリのインストール方法【Pycharm使用】

補足⑤ Pythonで読み込むデータの作成方法

Pythonで扱うCSVファイルの作成方法は以下のページで解説しています．

》【Python用】CSVファイルの作り方

Python 多変量解析 統計学
RELATED POST