標準誤差とは
標準誤差とは標本平均のばらつきを示す統計量になります.
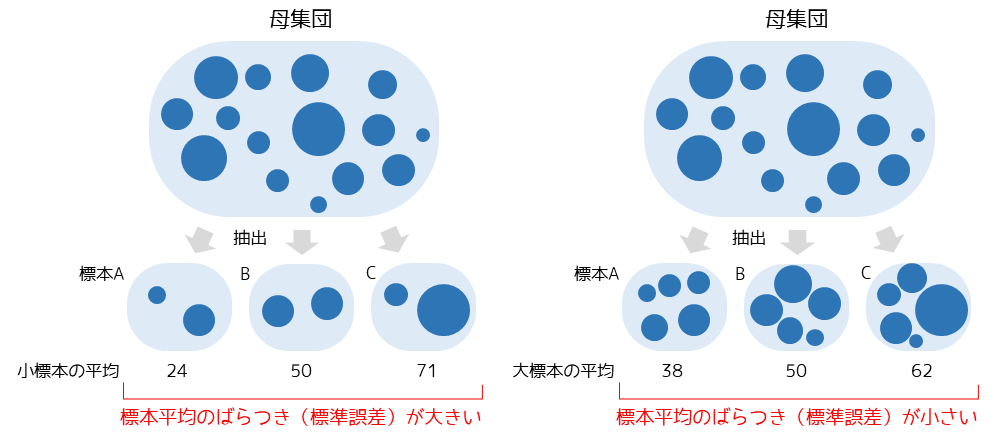
標準誤差は標本のサンプルサイズが大きいほど小さくなります.つまり,標本平均から推定した母平均の精度が上がることを意味します.
サンプルサイズが大きくなると標準誤差が小さくなるのは,以下の標準誤差の公式からも明らかです.

ここで標準偏差は標本自体のばらつきを示す指標で,自由度はサンプルサイズになります.
標準誤差(standard-error)は”SE”で表されることもあります.
Excelを用いた標準誤差の計算方法
Excelを用いた標準誤差の求め方について解説します.Excelでは2つの方法で標準誤差を求めることができます.
① 標準偏差から求める
標準誤差は標準偏差とサンプルサイズを用いることで求めることができます.
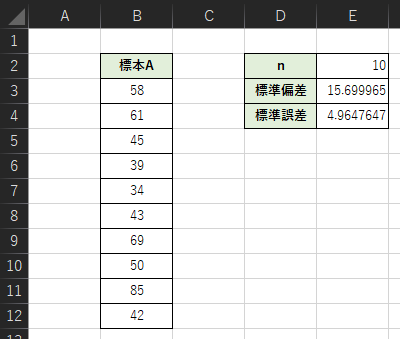
入力式は以下のようになります.
・E2セル:=COUNT(B:B)
・E3セル:=STDEV.S(B3:B12)
・E4セル:=E3/SQRT(E2)
標準偏差はSTDEV.S関数を用いて,データから直接計算することができます.
② データ分析ツールを用いる
Excelのデータ分析ツールでは,標準誤差を含む基本統計量を一括で計算することができます.
基本統計量を求めるデータ分析ツールを選択するために,「データ」タブの「データ分析」をクリックします.

次に出てきた「データ分析」ウィンドウから,「基本統計量」をクリックして「OK」を選択します.
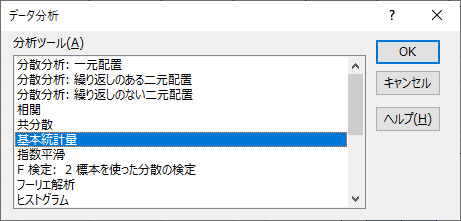
基本統計量の設定項目に必要な値を入力します.「統計情報(S)」には必ずチェックを入れてください.
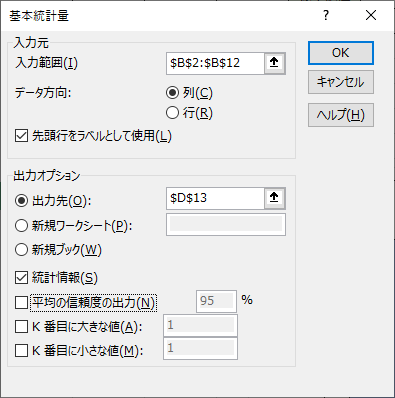
「OK」を選択すると以下のような表が出力されます.出力結果の2行目に標準誤差があります.
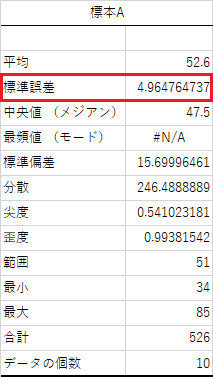
①と同じデータを用いて計算しているため,①で求めた値と一致しています.
以上がExcelを用いた,標準誤差の求め方です.
標準誤差と母平均の信頼区間の関係
標準誤差と母平均の信頼区間の関係性について解説します.
サンプルサイズが大きい(n=30以上)場合は,標本平均は母平均を中心とした正規分布に従います(中心極限定理).標本平均が正規分布に従う場合,母平均の95%信頼区間は以下の図のように求めることができます.
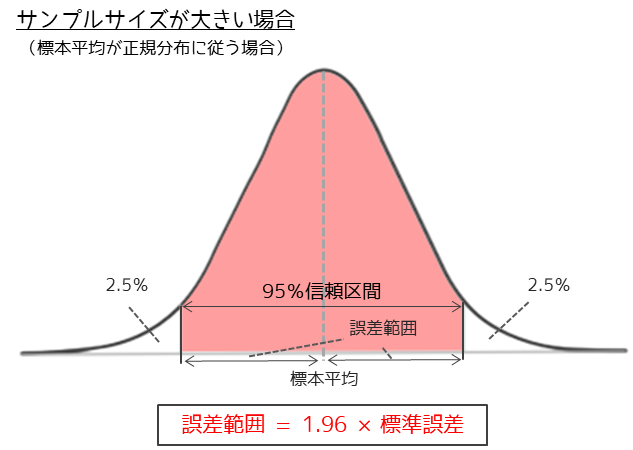
データから得られる標本平均から信頼区間の端までの長さである誤差範囲は,1.96×標準誤差で計算することができます.(標準誤差の約2倍が誤差範囲になります.)
99%信頼区間を求める場合の誤差範囲は,2.58×標準誤差で計算できます.
標本平均が正規分布に従わない場合は,標準誤差を用いて母平均の信頼区間を計算することはできません.
標準誤差のグラフ(エラーバー)
標準誤差はエラーバーを用いて図示することができます.
標準誤差のエラーバーは以下の図ように,平均値を示した棒グラフと組み合わせて表現します.
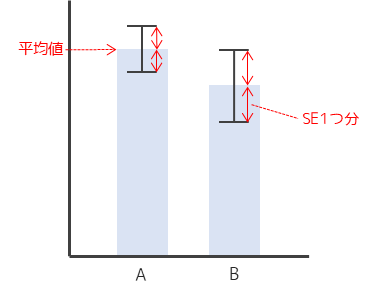
エラーバーについては以下のページで詳しく解説しています.









