様々な時系列モデル
時系列分析のモデルには様々なものがあり,ARIMAやVARなどの古典的な自己回帰モデルから2017年頃に開発されたProphetなどの最新のものまであります.
概観としては自己回帰モデル(以下の表のARIMA系からARCH系まで),状態空間モデル,機械学習モデルなどがあります.それぞれのモデルの特徴を早見表にまとめましたが,特にビジネス分野において雑に時系列分析・予測を行いたい場合はProphetが圧倒的におすすめです.
| ARIMA系 | VAR | ARCH系 | 状態空間モデル | Prophet | |
|---|---|---|---|---|---|
| 予測精度(短期) | ○ | ○ | – | ○ | ○ |
| 予測精度(長期) | △ | △ | – | ○ | ○ |
| 可解釈度 | ○ | △ | ○ | △ | △ |
| 手軽さ | ○ | ○ | △ | × | ◎ |
| 非定常過程 | ○ | △ | × | ○ | ○ |
| 主な用途 | 将来予測 | 因果関係の分析 | ボラティリティの予測 | 将来予測 | 将来予測 |
自己回帰モデルは学術研究でよく用いられ,解釈のしやすさが最大の特徴となります.状態空間モデルはアルゴリズムが自己回帰モデルより難解ですが,時系列分析以外の様々な分野で使用される汎用的なモデルになります.
VARやARCH系のモデルはそれぞれ将来予測ではなく,因果関係の分析やボラティリティ・VaRの算出といった目的のために利用されることが多いです.
非定常過程については以下のページで解説しています.
ARIMA系
ARモデル(自己回帰モデル)
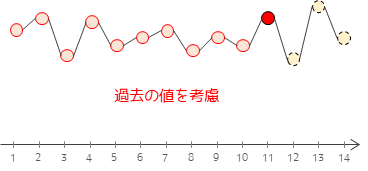
ARモデル(Autoregressive Model,自己回帰モデル)は時系列分析において最も基本的なモデルで,過去の時点でのデータが現在のデータに影響を与えるという考え方に基づいたモデルです.ARモデルはある一定値の周りで一定パターンの推移を繰り返すデータ(定常過程)のモデリングに適しています.
逆に言うと,定常過程ではない長期変動や季節変動があるデータのモデリングには適していません.
MAモデル(移動平均モデル)
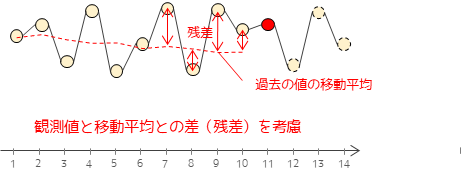
MAモデル(Moving average model,移動平均モデル)ある時点の時系列データがその時点の誤差項のみに影響されるモデルです.つまり,過去の移動平均と実測値との差の加重平均した値が現在の値に対して影響を与えます.
ARモデルと同様に,定常過程ではない長期変動や季節変動があるデータのモデリングには適していません.
ARIMAモデル(自己回帰和分移動平均モデル)
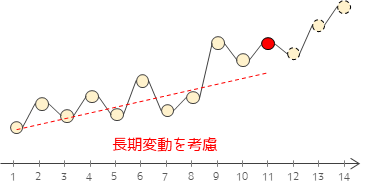
ARIMA(Autoregressive integrated moving average model,自己回帰和分移動平均モデル)モデルは,自己回帰モデルと移動平均モデルを組み合わせた時系列分析のモデルです.自己回帰モデルと同様に,過去のデータが未来のデータに影響を与えるという考え方に基づいています.しかし,ARIMAモデルは自己回帰モデルだけではうまく予測できないような長期変動を含む時系列データ(非定常過程)にも適用できます.ARIMAモデルでは差分をとることで,長期変動を除去し定常過程に変換します.
ARIMAモデルは古典的な自己回帰モデルの一種ですが,機械学習やディープラーニングが得意としない小さなデータセットに対しても性能が良いため,様々な時系列データに対して現在でも多く使用されます.
ARIMAモデルで時系列分析を行う場合はボックス・ジェンキンス法という,高い精度でモデルを作成するための手順がよく行われます.
SARIMA(季節変動自己回帰和分移動平均モデル)
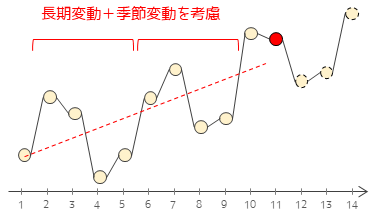
SARIMA(Seasonalk autoregressive integrated moving average model,季節変動自己回帰和分移動平均モデル)モデルは,ARIMAモデルに季節成分を追加したモデルです.SARIMAモデルでは,季節性のパターンを捕捉するために,過去の季節性の誤差を含めたモデルを構築します.
VAR(ベクトル自己回帰モデル)
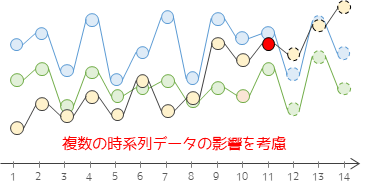
VAR(Vector auto regressive model,ベクトル自己回帰モデル)は複数の時系列データを同時に分析するための統計モデルです.例えば,株価や為替レートなどの相互に影響しあうデータを同時に扱えるのがVARモデルの強みです.また,異なる時系列データの相互作用を捉えることができるため,ビジネスやマクロ経済学などで活用されます.
VARモデルでは作成したモデルを用いて,インパルス応答関数やグレンジャー因果性検定を行うことで変数間の因果関係を分析することができるのが大きな特徴です.
ARCH系
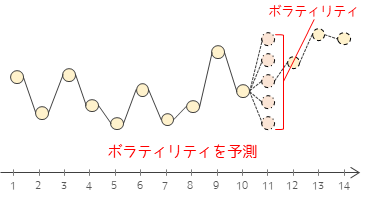
ARCH(Autoregressive Conditional Heteroskedasticity,自己回帰条件付き不均一分散)系モデルはボラティリティを予測するためのモデルです.ボラティリティとは金融分野における価格変動の大きさや度合いのことを指します.例えば,株価が一日で大きく上下するときその株は”ボラティリティが高い”と言います.
ARCH系モデルにおいては将来のボラティリティは過去のボラティリティにより影響を受けるという仮定のもと分析を行います.ARCH系モデルの中でも特に,過去の誤差項と分散に依存するGARCHモデルがよく使われます.
状態空間モデル
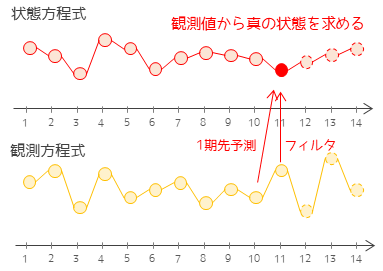
状態空間モデルは,時系列分析においてデータの背後にある「状態」というものを考え,その状態がどのように時間的に変化するかをモデル化する手法です.
状態空間モデルでは,現在の状態を表す「状態ベクトル」と呼ばれる変数を定義し,時間の経過に伴い状態ベクトルがどのように変化するかを表す「状態方程式」と,状態に基づいて生成された観測誤差を表す「観測方程式」が用いられます.
また,状態空間モデルは多くの時系列データに適用可能な柔軟性があるため,様々な分野で広く利用されています.状態空間モデルには様々なアルゴリズムがあり,よく使われるものとしては以下の3つがあります.
・カルマンフィルター
・パーティクルフィルター(粒子フィルター)
・EMモデル(expectation-maximization algorithm)
Prophet
Prophetは,Facebookが開発したオープンソースの時系列予測アルゴリズムで,時系列データの予測に特化しています.Prophetは,長期変動,季節変動,イベントなどの様々な要素を考慮した柔軟なモデルを提供しており,データの欠損値にも対応できます.
Prophetは様々なパラメータを分析者が設定する必要なく,長期的な予測も可能なためビジネス・学術研究を含め様々な場面で利用されています.
時系列モデルを扱うならStaatApp
統計解析アプリStaatAppでは本ページで紹介した時系列モデルを,プログラミングを行わずクリック操作だけで扱うことができます.ARIMAモデル機能は無料で利用することができます.
時系列データを手軽に分析したいという方におすすめです.










