相関比とは
相関比とは,2つの変数間の相関の強さを測る指標です.量的データとカテゴリーデータの2つの変数の関係性を調べる際に用います.

相関比は0から1の値を取り,値が大きいほど2つの変数の相関が強いことを表します.
相関比の考え方について年齢と副業の種類というデータを例にすると以下のようになります.
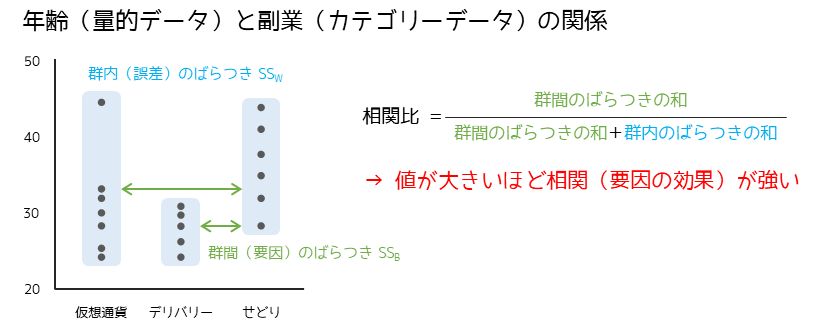
カテゴリーデータ内(群内)の量的データのばらつきに対して,カテゴリーデータ間(群間)のばらつきが大きい場合にカテゴリーデータと量的データの関連性(相関)が強いと判断します.
統計学的に相関比に対する基準はありませんが,目安としては以下のようになります.
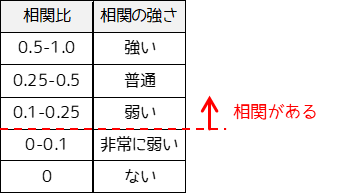
一般的には相関比が0.1以上ある場合に,2つの変数に相関関係があると判定します.相関係数が0でない(0.1などでも)場合,「2つの変数に相関関係がある」と言います.
計算結果を間違えたくない方へ
Excelを用いた計算方法より簡単・正確に,相関比・無相関の検定結果を調べることができる統計解析アプリStaatAppを配布しております.
StaatAppでは相関比以外にも様々な統計解析をクリックするだけで実行することができます.初めての方はほぼ全ての機能を無料で利用できるので,お気軽にダウンロードしてお使いください!
》統計解析アプリStaatApp
》StaatAppで相関比・無相関の検定を行う
例題の設定
具体的に計算手順を説明するために,例題を設定します.
以下のように社会人18人の年齢と行っている副業に関するデータがあるとします.
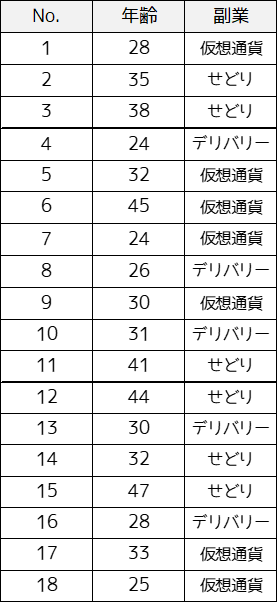
相関比を求めることで,年齢と副業の種類の相関関係を調べます.
Excelを用いた計算方法
Excelを用いた相関比の求め方を解説します.
以下のような表を作成して,相関比η2(イータ)とp値を求めます.仮想通貨→A,デリバリー→B,せどり→Cとして入力しています.
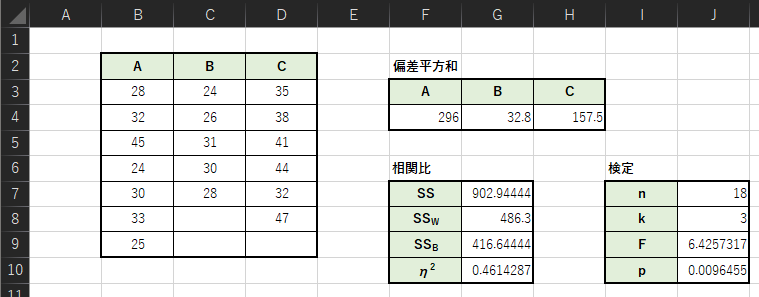
入力式の例は以下になります.
・F4:=DEVSQ(B3:B9)
・G7:=DEVSQ(B3:D9)
・G8:=SUM(F4:H4)
・G9:=G7-G8
・G10:=G9/G7
・J9:=(G9/(J8-1))/(G8/(J7-J8))
・J10:=F.DIST.RT(J9,J8-1,J7-J8)
計算手順について説明します.
① データをカテゴリーデータごとに入力する【B-D列】
カテゴリーデータごとに列を分けてデータを入力します.
② 各群内の偏差平方和を求める【F-H4】
各群(列)ごとの偏差平方和を求めます.偏差平方和はばらつきを表す統計量です.
ExcelではDEVSQ関数を用いて求めることができます.
③ 全体の偏差平方和を求める【G7】
データ全体の偏差平方和を求めます.②と同様に,DEVSQ関数を用いて求めます.
④ 各群間の偏差平方和を求める【G8】
群(列)間の偏差平方和を求めます.データから直接計算することもできますが,今回は以下の関係を用いて簡単に求めます.
全体の偏差平方和 SS = 群内の偏差平方和 SSW + 群間の偏差平方和 SSB
全体の偏差平方和から群内の偏差平方和の差が群間の偏差平方和になります.群内の偏差平方和は②で求めた各群の偏差平方和の合計値になります.
⑤ 相関比を求める【G9】
群内の偏差平方和SSBと群間の偏差平方和SSWを用いて相関比を求めます.相関比を求める式を以下になります.
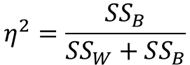
例題では相関比η2=0.461..となり,年齢と副業の種類には相関があるといった結論を得ることができます.
⑥ 検定統計量を求める【J9】※ 相関比の検定については補足①で解説します.
相関比の検定統計量Fを求めます.検定統計量は以下の式で求めることができます.
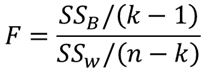
kは群数(カテゴリーデータの種類数),nは全データ数になります.
⑦ p値を求める【J10】
検定統計量からp値を求めます.検定統計量Fは近似的にF分布に従うため,Excelでは検定統計量からF分布の上側確率を求めるF.DIST.RT関数を用います.
F.DIST.RT関数の書き方:=F.DIST.RT(“検定統計量”,k-1,n-k)
k-1は群間の偏差平方和の自由度,n-kは郡内の偏差平方和の自由度を表します.
以上がExcelを用いた計算手順になります.
補足① 検定方法とp値について
相関比に対する仮説検定では,求めた相関係数が統計学的に有意であるかを判定します.
帰無仮説は「2つの変数に相関関係はない」となり,有意差がある場合帰無仮説は棄却され対立仮説である「2つの変数に相関関係がある」という結論を得ることできます.
相関比の検定統計量は群内の偏差平方和と群間の偏差平方和の比で求めることができます.偏差平方和の比(=分散の比)はF分布に従います.
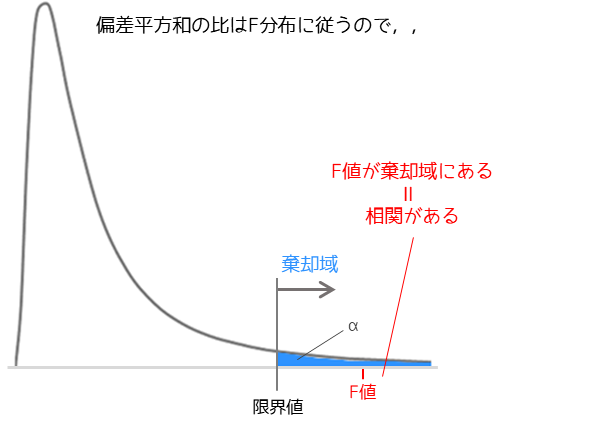
例題ではp値が0.0096..なので有意水準α=0.05において帰無仮説は棄却され,2つの変数に相関関係があるという結論が得られます.
補足② 順位相関係数,連関係数との違い
質的データの関連性を調べる類似手法として,順位相関係数や連関係数があります.
それぞれの手法は以下のデータの関連性を調べる際に用います.
| 相関係数 | 変数A | 変数B |
| ピアソンの積率相関係数 | 量的データ | 量的データ |
| 相関比 | 量的データ | カテゴリーデータ |
| スピアマンの順位相関係数 | 順位データ | 順位データ |
| ケンドールの順位相関係数 | 順位データ | 順位データ |
| クラメールの連関係数 | カテゴリーデータ | カテゴリーデータ |










