母集団とは
統計学では調べたい対象全体を母集団と言います.
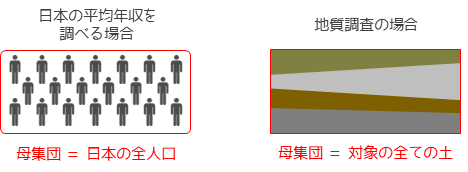
日本の平均年収を調べたい場合は,調べたい対象は全日本人となり母集団は日本の全人口になります.地質調査の例では,対象範囲全ての土が母集団になります.
母集団には有限母集団と無限母集団があります.
有限母集団は調べたい対象の数に限りがある場合の母集団になります.平均年収の例では日本の人口には限りがあるため,有限母集団となります.地質調査においても調査範囲には限りがあり,全ての要素(土)を調査することは物理的には可能であるため有限母集団となります.
無限母集団は調べたい対象の数に限りがない場合の母集団です.無限母集団の具体例としては,サイコロの出た目から得るデータになります.サイコロを投げる実験は無限に繰り返すことができ,母集団の要素の数に限界がありません.
全数調査の難しさ
母集団の特性を完全に調べるためには,母集団の全ての要素を調べる必要があります.母集団の全ての要素を調べることを全数調査と言います.全数調査を行った場合は,得られたデータから統計量を算出して母集団の特性を捉えることができます(記述統計学).
記述統計学における大きな問題が,必ずしも全数調査を行うことができないという点です.日本の平均年収の例では,全数調査を行うためには約1億人を対象に調査を行う必要があります.

約1億人を対象に調査を行うためには,時間的・金銭的なコストが莫大にかかり実現不可能です.母集団が1億人ではなく1,000人であっても,全数調査を行うためにはコストが必要となります.
無限母集団についてはそもそも全数調査を行うことは不可能です.
全数調査を行うことができない,コストがデータ分析の目的に見合っていない場合に行うのが標本調査になります.
日本で最も大規模に行われている全数調査は,5年に一度行われる国勢調査になります.国勢調査は日本の人口を正確に把握するために膨大な人と時間,税金を使って行われます.国勢調査で得られるデータ(主に人口)にはそれだけのコストに見合った価値があるということです.
標本・標本調査とは
標本調査とは母集団の一部を抽出(サンプリング)して,抽出した標本(サンプル)から母集団の特性を調べることです(推測統計学).
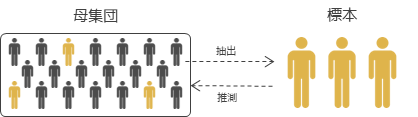
全数調査と比較して母集団の一部のみのデータを得られれば分析を行うことが可能であるため,データ分析に必要なコストを大きく下げることができます.
標本調査は抽出と推測の2つの重要な工程があります.
標本調査を正確に行うためには,母集団と同じ特性を示すように標本を抽出する必要があります.母集団から偏り(バイアス)のある標本を抽出した場合,母集団の特性がわからなくなってしまいます.平均年収を調べる際に,若年層ばかりを抽出した標本から得られた平均年収は日本人の平均年収とは言えません.抽出はデータ分析を行う際に疎かになりがちですが,推測と同様に重要な工程になります.
推測は区間推定や仮説検定,多変量解析などの様々なデータ分析を行う工程です.データの種類やデータ分析の目的に合った手法を選択することが重要です.分析結果を公表する際は,結果をどのように解釈してどのように表現するのかも標本調査として重要になります.
【補足】サンプルサイズとサンプル数の違い
サンプルサイズ(標本サイズ)とサンプル数(標本数)は,似た言葉であるため混合されがちですが統計学においては全く異なる意味を持ちます.
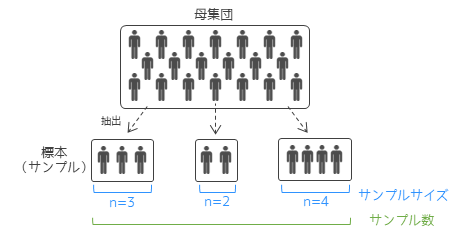
サンプルサイズは標本内の要素数になります.サンプルサイズは”n”で表され,図中右の標本はn=4になります.サンプル数は抽出した標本の数になります.図では母集団から3回抽出して標本が3つあるため,サンプル数は3になります.









