分散分析とは
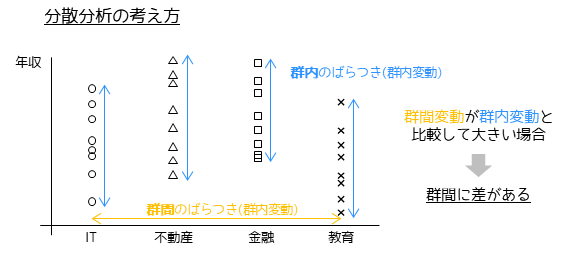
分散分析の考え方の基本は,群内変動と群間変動の比の検定です.1つの群のデータのばらつきを示す群内変動に対して,各群のデータのばらつきを示す群間変動が大きい場合,群間に差があると判断します.
図のように各業界内での個人間の年収のばらつき(群内変動)に対して,各業界間の平均年収のばらつき(群間)の比を調べることで,各業界間の平均年収の差を調べることができます.
分散分析にはいくつかの種類があり,主に2つの目的がある統計解析手法になります.
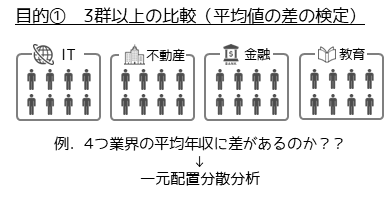
分散分析の1つ目の目的は3群以上の比較になります.2群を比較する手法として一般的なt検定は,3群以上の比較に用いることができません.例えば4つの業界の平均年収に差があるかを調べたい場合は,一元配置分散分析を行います.
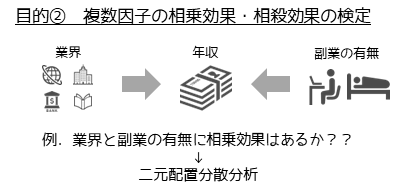
分散分析の2つ目の目的は複数因子の相乗効果・相殺効果(交互作用)を調べることです.例えば社会人の所属する業界と副業の有無には,相乗効果があるのかを年収という値を利用して調べることができます.
要因・因子・水準とは
分散分析の種類は様々な種類があり,3つの用語を用いて説明されます.
・要因
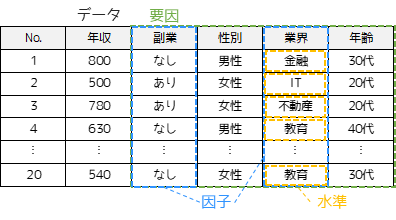
データの値に影響を与えると考えられる全項目です.
・因子
要因の中の母平均に差を与えると考えられる項目です.つまり,分散分析を行う際に比較したい項目になります.目的①の例では”業界”が,目的②では”業界”・”副業有無”の2つが因子になります.
・水準
1つの要因に含まれる各群のことです.因子の1つである”業界”には4つの業界があったため,水準は4になります.
分散分析の分類
分散分析では因子の数によって種類があります.
・一元配置分散分析
1つの因子の場合に分析する方法です.目的①のような場合に行います.
・二元配置分散分析
2つの因子の場合に分析する方法です.目的②のような場合に行います.
・多元配置分散分析
3つ以上の因子の場合に分析する方法です.
分散分析をExcelなどの手計算で行う際は,以下のように水準(群)ごとにデータを整理します.そして,分析の目的が群項目Aの群間の比較である場合は,因子は群項目Aの1つなので一元配置分散分析を行います.
分析の目的が群項目Aと群項目Bがお互いに影響を及ぼしているか調べるである場合,群項目Aと群項目Bは因子となり,因子が2つなので二元配置分散分析を行います.

反復測定の場合
分散分析は因子の数以外に,因子が反復測定されたデータかどうかによって分類されます.
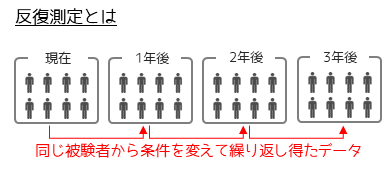
反復測定とは同じ被験者・同一個体に対して条件を変えてデータを得ることです.統計学では”対応のある”・”繰り返しのある”と言うことも多いです.
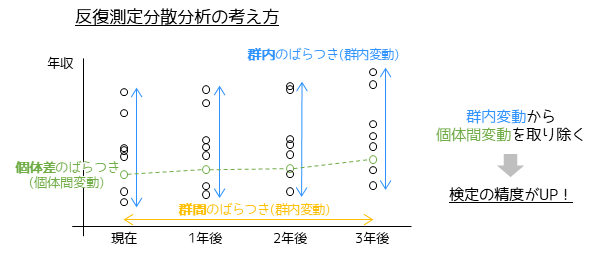
反復測定分散分析では,個体差のばらつき(個体間変動・被験者間変動)を考慮します.対応のない分散分析に対して,群内変動から個体間変動を取り除くことで検定の精度を高めることができます.
反復測定分散分析においても因子の数によって,反復測定一元配置分散分析や反復測定二元配置分散分析といった種類があります.
反復測定で得られたデータの分析においては,近年は一般化線形混合モデルという手法がよく用いられます.詳しくは以下のページで解説しています.
分散分析の一覧
分散分析の一覧は以下のようになります.
| 分散分析の種類 | 因子数 | 対応のある | Excel | StaatApp |
| 一元配置分散分析 | 1 | ○ | ○ | |
| 反復測定一元配置分散分析 | 1 | ○ | ○ | |
| 二元配置分散分析 | 2 | ○ | ○ | |
| 反復測定二元配置分散分析 | 2 | ○ | ○ | |
| 多元配置分散分析 | 3以上 | ○ | ||
| 反復測定多元配置分散 | 3以上 | ○ |
Excel列に○が付いている分散分析は,分析ツールを用いることで比較的簡単に実行可能です.
StaatApp列に○が付いている分散分析は,統計解析アプリStaatAppで実行可能な分散分析です.StaatAppはクリックするだけで統計解析を簡単に行うことができるアプリになります.Excelで必要なデータの整形が不要で,反復測定一元配置分散分析や多元配置分散分析も行うことができます.
》StaatAppで行う分散分析
》統計解析アプリStaatApp
一元配置分散分析とは
一元配置分散分析とは,扱うデータの因子が1つの場合に行う分散分析です.
一元配置分散分析の帰無仮説は「各群の母平均は等しい」となり,対立仮説は「各群の母平均は異なる」となります.ここで重要なのが,検定結果に有意差があり対立仮説が採択される場合に得られる結論は,各群のうちどれかの郡の母平均は異なるとなることです.分散分析では,3群以上の場合にどの群とどの群が異なるかまでは判断することができません.これらのことを判断したい場合は,「多重比較」という分析を行います.

3つ以上の群に違いがあるか判断したい場合は一元配置分散分析を行い,有意差があれば多重比較を行いどの群に違いがあるかを判断します.2つの群ごとにt検定を行っている論文もありますが,これは統計学的に間違いになります.
3つ以上のグループに違いがあるか判断したい場合は,一元配置分散分析を行ってから多重比較を行うと説明しました.実運用(特にアンケート結果など)では,一元配置分散分析の結果で得られる「どれかの群が異なる」では無く,「どのグループが異なるか」を判断したい場合が多いです.
このような目的の場合はいきなり多重比較を行っても問題ありません.注意点としては,多重比較の中でもDunnet法やTukey-Kramer法といったF検定の考え方が入っていない検定方法を選択する必要なあります.
分散分析は予め設計された実験に対して行う解析手法になります.例えば医学分野において,プラセボを投与したグループ(対照群)と,効果を知りたい新薬を投与したグループ(実験群)の比較をする際によく用いられます.
》Excelで行う一元配置分散分析
》多重比較についてさらに詳しく
二元配置分散分析とは
二元配置分散分析とは,扱うデータの因子が2つの場合に行う分散分析です.二元配置分散分析は一元配置分散分析のように群間の比較に加えて,因子がお互いに影響を及ぼしているか(交互作用)を判断する際に行います.
二元配置分散分析の帰無仮説は,以下の3つになります.
「群項目Aの各群の母平均は等しい」
「群項目Bの各群の母平均は等しい」
「群項目Aと郡項目Bは交互作用がない」
対立仮説は以下の3つです.
「群項目Aの各群の母平均は異なる」
「群項目Bの各群の母平均は異なる」
「群項目Aと群項目Bは交互作用がある」

二元配置分散分析の特徴である交互作用について説明します.分散分析の目的②では因子は業界と副業の有無でした.ここで,各セルの値つまり水準ごとの平均年収をプロットしたグラフを作成します(業界の水準数を2とした場合).作成したグラフは以下のように縦軸に平均年収,横軸に副業の有無をとったグラフになります.

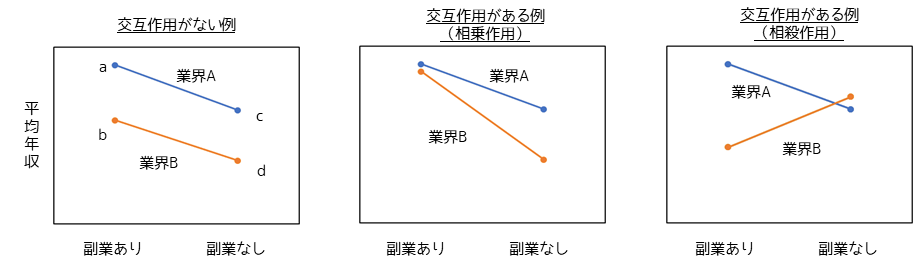
交互作用に有意差が無い場合,つまり交互作用がない場合は左のようなグラフとなりお互いの因子が影響しあっていないのでそれぞれの因子の影響だ,けを考えれば良いとなります.例えば,交互作用がなく副業の有無という因子が平均年収に対して,有意という結果を得られた場合,t検定などで群間(副業がある人・家族が無い人)の比較を行うことができます.
交互作用に有意差がある場合,つまり交互作用がある場合は中央や右のグラフとなりお互いの因子が影響しあっているので,両者を切り離して考えることはできません. 例えば,交互作用があり副業の有無という因子が有意という結果を得られた場合, もう1つの因子の影響も考えられるため結果は参考程度となります.この場合,水準ごとに分類した4つの群(表中のa,b,c,d)の多重比較を行い,群間の比較を行うことが可能です.
二元配置分散分析において,交互作用の有無は群間の多重比較を行うことができるかといった点で非常に重要です.
分散分析を行う前提条件
分散分析を行う際の扱うデータの前提条件について紹介します.
① 正規分布に従う
分散分析は,パラメトリックな検定になります.用いるデータが正規分布に従うと仮定できる場合に使うことができます.正規分布でない場合は,ノンパラメトリック検定であるクラスカル・ウォリスの検定を行います.
② 比較するグループの分散が等しい
比較するグループの分散が等しい場合に分散分析を行います.3群以上の分散はバートレット検定で調べることができます.分散が等しくないときは,ウェルチの検定を行います.










