PythonのScipyライブラリを用いた,データの正規性の調べ方について解説します.
グラフを用いる方法と仮説検定を用いる方法を解説します.
正規性の調べ方
データの正規性を調べる方法としては,グラフを用いる方法と仮説検定の2つがあります.
グラフを用いる方法では主にヒストグラムやQ-Qプロット(Quantile-Quantile Plot)を作成してデータの分布を視覚化することで正規分布に従うか判断します.
仮説検定では主にシャピロ・ウィルク検定やコルゴモロフ・スミルノフ検定が使われます.仮説検定では「データの母集団の分布は正規分布に従う」という帰無仮説を設定して,有意差がある場合に正規性がないと判断します.
どちらの方法もメリット・デメリットがあり,正規性の調べ方に最適な手法・判断基準はないのが現状です.
例題で用いるデータ
本ページでは以下のようなExcelで作成したデータの検証を行います.1から100までの値を正規分布にある程度従うように入力した値です.見切れていますが,各群のサンプルサイズは100になります.
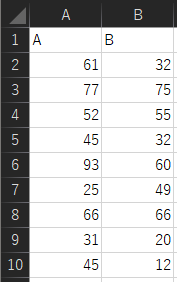
ExcelファイルからPythonで読み込ませるCSVファイルに変換する方法は,以下のページで解説しています.
Pythonを用いた記述例
Pythonでは以下のようにプログラムを作成することで,データの母集団が正規分布に従うか調べることができます.詳細は次章以降で解説します.
# ライブラリのインポート
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt
# データの読み込み
df_sample = pd.read_csv("nomal.csv")
# ヒストグラムの作成
plt.hist(df_sample["A"])
plt.show()
# Q-Qプロットの描画
stats.probplot(df_sample["B"], dist="norm", plot=plt)
plt.show()
# シャピロ・ウィルク検定
result1 = stats.shapiro(df_sample["A"])
print(result1)
# コルゴモロフ・スミルノフ検定
result2 = stats.ks_1samp(df_sample["A"], stats.norm.cdf)
print(result2)使用するライブラリは以下になります.
・Pandas(データ操作)
・Scipy(グラフ作成・仮説検定)
・Matplotlib(グラフ描画)
Pythonでプログラムを作成・動かす方法は補足をお読みください.
ヒストグラムの作成・描画
# ヒストグラムの作成
plt.hist(df_sample["A"])
plt.show()PythonではMatplotlibのhist関数を用いることで,ヒストグラムを作成することができます.引数には読み込ませたデータを指定します.例ではデータフレームの列を指定します.
ヒストグラムは以下のように描画されます.中央に向かって山型で正規分布風な分布であることがわかります.
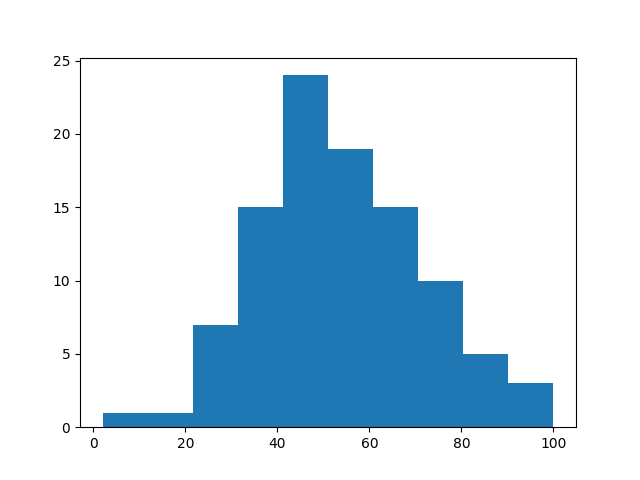
Q-Qプロットの作成・描画
# Q-Qプロットの描画
stats.probplot(df_sample["A"], dist="norm", plot=plt)
plt.show()Q-QプロットはScipyのstatsモジュールを用いて作成します.正規分布と比較するQ-Qプロットを作成する場合は,第一引数のdf_sample[“A”]のみ自分のデータに合わせて修正してください.
Q-Qプロットは以下のように描画されます.
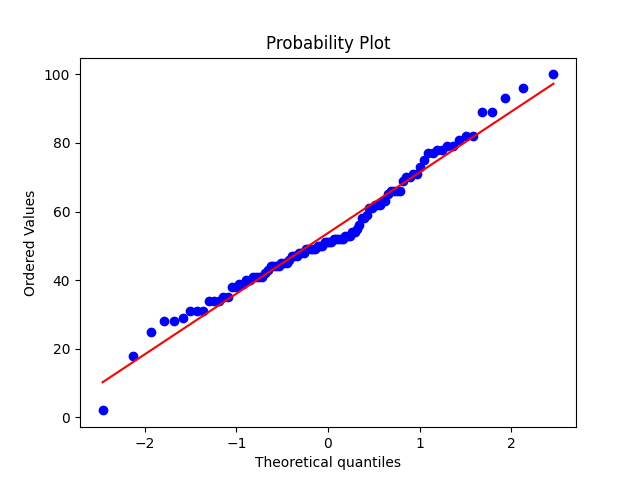
ある程度一直線上にプロットが分布しているため,データは正規性があると判断することができます.
シャピロ・ウィルク検定の実行
# シャピロ・ウィルク検定
result1 = stats.shapiro(df_sample["A"])
print(result1)
-->
ShapiroResult(statistic=0.9791301488876343, pvalue=0.1137021854519844)シャピロ・ウィルク検定はScipyのstatsモジュールを用いて行います.引数には読み込ませたデータを指定します.例ではデータフレームの列を指定します.
実行結果として,print関数を用いて検定統計量とp値が出力されます.p値\(\geq\)0.05であるため,有意水準α=0.05において「データの母集団が正規分布に従わないと言うことはできない」といった結論を得ることができます.
コルゴモロフ・スミルノフ検定
# コルゴモロフ・スミルノフ検定
result2 = stats.ks_1samp(df_sample["A"], stats.norm.cdf)
print(result2)
-->
KstestResult(statistic=0.99, pvalue=2.0000000000001775e-200)コルゴモロフ・スミルノフ検定はScipyのstatsモジュールを用いて行います.正規分布と比較を行う場合,1標本のコルゴモロフ・スミルノフ検定である,ks_1samp関数を用います.第一引数には読み込ませたデータを指定します.第二引数は正規分布との比較を行う場合は記述例の通りです.
実行結果として,print関数を用いて検定統計量とp値が出力されます.p値<0.05であるため,有意水準α=0.05において「データの母集団が正規分布に従わない」といった結論を得ることができます.
一般的にはサンプルサイズが小さい場合は,シャピロ・ウィルク検定の方が厳しい結果になりやすい(有意差が出やすい)と言われていますが,今回の例では逆の結果となりました.
補足 PyCharmを用いた実行環境の構築
Pythonを初めて使う方や,自分のPCにPython・PyCharmが入っていない方は以下のページで解説している手順で実行環境の構築を行ってください.
初めて触る方にもわかりやすいようにPyCharmを用いた手順となっています.
本ページでは,”pandas”や”matplotlib”,”Scipy”というライブラリを使用します.インストール方法が分からない方は,ライブラリのインストールを参考にしてください.
》実行環境の構築方法【Pycharm使用】
》ライブラリのインストール方法【Pycharm使用】









