非階層クラスター分析の具体的な計算方法についてPythonのsklearnライブラリを用いて解説します.
結果の見方や階層クラスター分析との違いについても解説しています.
階層クラスター分析については以下のページで解説しています.
例題の設定
クラスター分析を用いた統計解析を説明するために,以下の例題を用います.
「社会人21人に対して,副業の有無・収入・性別・年齢・結婚有無についてのデータを収集しました.収集したデータに対してクラスター分析を用いて,データの分類を行います.」
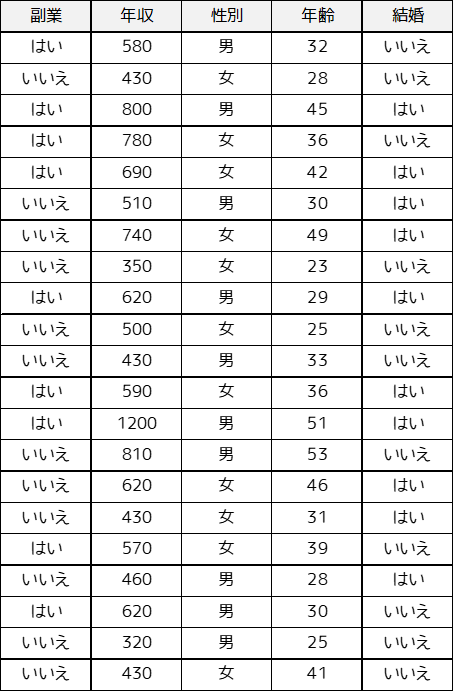
Pythonで読み込むせるデータ形式(CSVファイル)の作り方はこちら.
プログラムの作成・実行
Pythonを用いてプログラムの作成をします.
非階層クラスター分析に必要な記述例は以下になります.
# ライブラリのインポート
import pandas as pd
from sklearn.cluster import KMeans
# データの読み込み
workers = pd.read_csv("sample.csv")
# KMeansメソッドの実行
clu = KMeans(n_clusters=4)
# 結果の出力
workers["class"] = clu.fit_predict(workers)
print(workers)
# 各グループの平均値
print('各グループの平均値')
print(workers.groupby("class").mean())それぞれの記述内容について解説します.
① ライブラリのインポート
クラスター分析で用いるライブラリをインポートします.
2つのライブラリをインポートしますが,記述例と全く同じ内容で問題ありません.
# ライブラリのインポート
import pandas as pd
from sklearn.cluster import KMeans② データの読み込み
pd.read_csv関数を用いてCSVファイルの読み込み,データフレームに格納します.
データフレーム名(=の左側)は任意の値を入力します.””内は読み込むCSVファイル名を記述します.
# データの読み込み
workers = pd.read_csv("sample.csv")③ KMeansメソッドの実行
KMeansメソッドを用いて実行結果を新しく定義した変数に格納します.KMeamsメソッドは,非階層クラスター分析で最も一般的なk-means法を行うメソッド(関数みたなもの)になります.
【引数の書き方】
「n_clusters」:クラスター分析のクラス数を入力します.例題では4にしましたが,用いるデータや目的に合わせて設定してください.
# KMeansメソッドの実行
clu = KMeans(n_clusters=4)④ 結果の出力
fit_predict関数を用いて,データフレームに新しく定義した”class”列にクラスター番号を格納します.(workersの部分はデータの読み込みで定義したデータフレーム名を入力してください)
結果は,print関数を用いてコンソール上に出力します.
# 結果の出力
workers["class"] = clu.fit_predict(workers)
print(workers)
# 各グループの平均値
print('各グループの平均値')
print(workers.groupby("class").mean())以上がKMeansを用いた非階層クラスター分析になります.
PyCharmを用いている方は右上の「▶」ボタンを押すとプログラムが実行されます.
結果の見方
Pythonで非階層クラスター分析を実行すると以下のような結果が出力されます.
side_job income sex age married class
0 1 580 1 32 0 0
1 0 430 0 28 0 2
2 1 800 1 45 1 1
3 1 780 0 36 0 1
4 1 690 0 42 1 1
5 0 510 1 30 1 0
6 0 740 0 49 1 1
7 0 350 0 23 0 2
8 1 620 1 29 1 0
9 0 500 0 25 0 2
10 0 430 1 33 0 2
11 1 590 0 36 1 0
12 1 1200 1 51 1 3
13 0 810 1 53 0 1
14 0 620 0 46 1 0
15 0 430 0 31 1 2
16 1 570 0 39 0 0
17 0 460 1 28 1 2
18 1 620 1 30 0 0
19 0 320 1 25 0 2
20 0 430 0 41 0 2
各グループの平均値
side_job income sex age married
class
0 0.714286 587.142857 0.571429 34.571429 0.571429
1 0.600000 764.000000 0.400000 45.000000 0.600000
2 0.000000 418.750000 0.375000 29.250000 0.250000
3 1.000000 1200.000000 1.000000 51.000000 1.000000入力したデータに対して”class”という列が追加されてクラスター番号が出力されます.このクラスター番号が同じ値を持つデータが,同じクラスター(集団)となります.
クラスター分析ではグループ分けを行った後,各グループにどのような特徴があるのかを調べます.
各グループの平均値は,出力結果の下段になります.
例題では,クラスター番号0のグループは副業を行っている人が多いかつ若い社会人の集団であることが分かります.クラスター番号3のグループは全く副業を行っていない人の集団であることが分かります.
グループごとの平均値で特徴を見る以外にも,各グループごとに構成している人の割合(クラスター番号0では40代20代がそれぞれ1人など)を調べる方法もあります.
補足① クラスター分析とは
クラスター分析とは,データをいくつかのグループに分ける多変量解析になります.
グループの分け方によって様々な手法がありそれらをまとめてクラスター分析と言います.

クラスター分析によって分けられたグループにどのような特徴があるかは,分けられたグループのデータの構成や統計量(平均値や分散)を求めることで調べる必要があります.
補足② グループ分けの目的
クラスター分析では,何をグループ分けしたいかによってデータの作成方法(入力手順)が変わります.
例題では,社会人(サンプル)をグループ分けしました.調査項目(変数)をグループ分けして似ている調査項目を調べたい場合は行と列を入れ替えてクラスター分析を行う必要があります.
補足③ 階層クラスター分析と非階層クラスター分析
クラスター分析には階層クラスター分析と非階層クラスター分析があります.
階層クラスター分析では,グループ分けを樹形図として出力することができるので結果を視覚的に判断することが可能です.また,いくつのグループに分けるかを樹形図からつまりクラスタリング後に判断することが可能です.
一方で,階層クラスター分析は計算量が膨大になるためビッグデータを分析したい際には不向きです.階層クラスター分析を行うサンプル数の目安は100以下になります.
補足④ 類似度の求め方
クラスター分析において,グループ分けを行う基準が類似度になります.
非階層クラスター分析では,類似度の求め方としてk-meams法や超体積法があります.
最も代表的な手法は,k-meams法になります.k-meams法では,設定したクラスター数に大まかに分類し,各データとクラスターの重心の距離が別のクラスターの重心より小さくなるようにデータを分類します。
例題でも,k-means法を用いたクラスター分析を紹介しました.
補足⑤ 統計解析アプリ
本サイトではより手軽にクラスター分析を実行して,樹形図の作成を行うPC用アプリ(StaatApp)を販売しています.
詳細は以下のページで紹介しています.
》StaatAppで行うクラスター分析
》統計解析アプリStaatAppとは
補足⑥ PyCharmを用いた実行環境の構築
Pythonを初めて使う方や,自分のPCにPython・PyCharmが入っていない方は以下のページで解説している手順で実行環境の構築を行ってください.
初めて触る方にもわかりやすいようにPyCharmを用いた手順となっています.非階層クラスター分析では,”sklearn”というライブラリを使用します.インストール方法が分からない方は,ライブラリのインストールを参考にしてください.
》実行環境の構築方法【Pycharm使用】
》ライブラリのインストール方法【Pycharm使用】
補足⑦ Pythonで読み込むデータの作成方法
Pythonで扱うCSVファイルの作成方法は以下のページで解説しています.










