重回帰分析とは
重回帰分析とは,説明変数xが複数ある場合に行う回帰分析です.
重回帰分析の目的は主に2つになります.

1つ目の目的は目的変数に対する説明変数の影響度を調べることです.重回帰分析を行うことで,どの説明変数が目的変数に対してどの程度影響を与えているかがわかります.
2つ目の目的は得られた回帰式を用いて目的変数の予測を行うことです.重回帰分析を行うと切片と各説明変数の係数(偏回帰係数)が求められ,回帰式(モデル式)を作ることができます.この回帰式の各変数に値を代入することで,目的変数を予測することができます.
重回帰分析の手順
重回帰分析は以下の手順で行います.
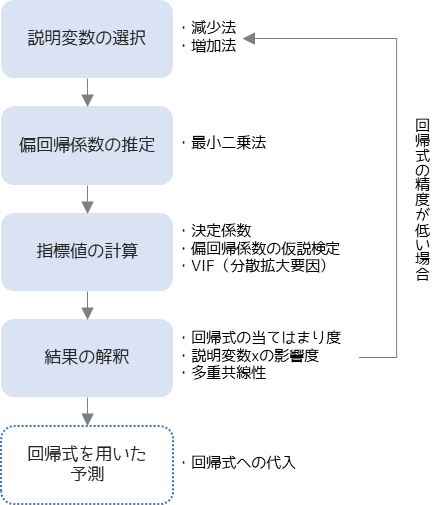
重回帰分析の行う前に,回帰式に含める説明変数を選択します.1回目は目的変数以外の全ての変数を説明変数に含めます.
偏回帰係数の推定では最小二乗法を用いて計算を行います.
偏回帰係数を推定したら回帰式の当てはまり度や,説明変数の影響度を統計的に判断するために決定係数などの指標値を計算します.
計算した指標値を用いて,推定した回帰式の正しさを解釈します.解釈した結果,回帰式が正しいと判断した場合は,回帰式を用いて目的変数の予測を行うことができます.
回帰式の精度が低い場合は,説明変数の選択からやり直します.説明変数の選択方法としては,減少法や増加法があります.
統計解析アプリで行なう重回帰分析
Excelでは標準偏回帰係数やVIFは数式を作成して計算する必要があります.統計解析アプリStaatAppでは,マウス操作だけで重回帰分析の実行,様々な評価指標やパラメータの算出,予測値の算出が行なえます.
詳細は以下のページで紹介しています.
》StaatAppで行う重回帰分析
》統計解析アプリStaatAppとは
例題の設定
具体的に重回帰分析の解説をするために,以下のように例題を設定をします.社会人10人の年収に関するサンプルデータになります.

「年収」に対する影響度を調べて,予測式を求めるために目的変数は「年収」として重回帰分析を行います.
Excelを用いた重回帰分析
Excelのデータ分析ツールを用いた重回帰分析の方法について説明します.
重回帰分析を行うツールを選択するために,「データ」タブの「データ分析」をクリックします.

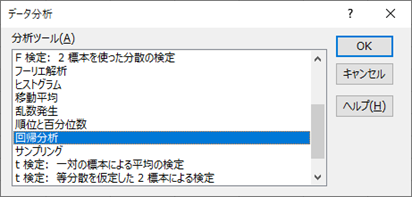
「データ分析」ウィンドウから,「回帰分析」をクリックして「OK」を選択します.
「回帰分析」における入力項目について説明します.入力例は以下のようになります.
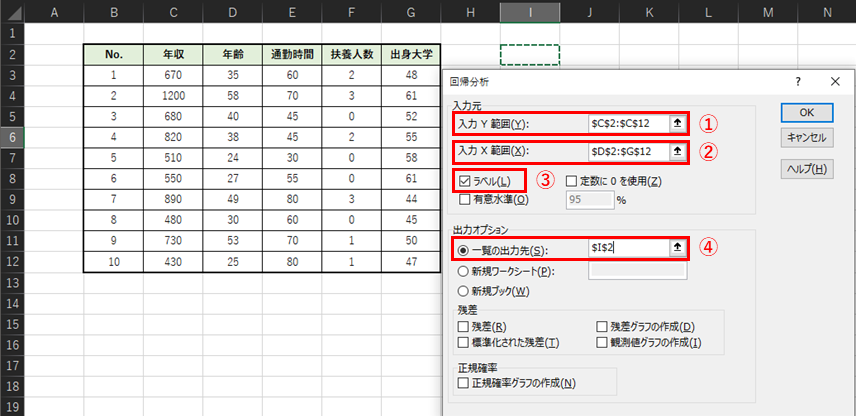
① 入力Y範囲
重回帰分析の目的変数が入力されたセルを選択します.
② 入力X範囲
重回帰分析の説明変数が入力されたセルを選択します.例題では,年齢・通勤時間・扶養人数・出身大学の4つ項目を説明変数とします.
③ ラベル
チェックを入れます.①②の選択範囲には,ラベル(項目名のセル)を含めて選択してください.
④ 一覧の出力先
重回帰分析の結果の出力先のセルを選択します.「出力オプション」では新しいワークシートを選択することもできますが,同じシートの空いているセルに出力する方が結果が見やすいためおすすめです.
その他の項目については,重回帰分析を行う上で必要無いので全てチェックを外してください.
入力が完了後「OK」をクリックすると重回帰分析が実行され結果が出力されます.
分析結果の見方(データ分析ツール)
ツール実行後,以下のような表が出力されます.
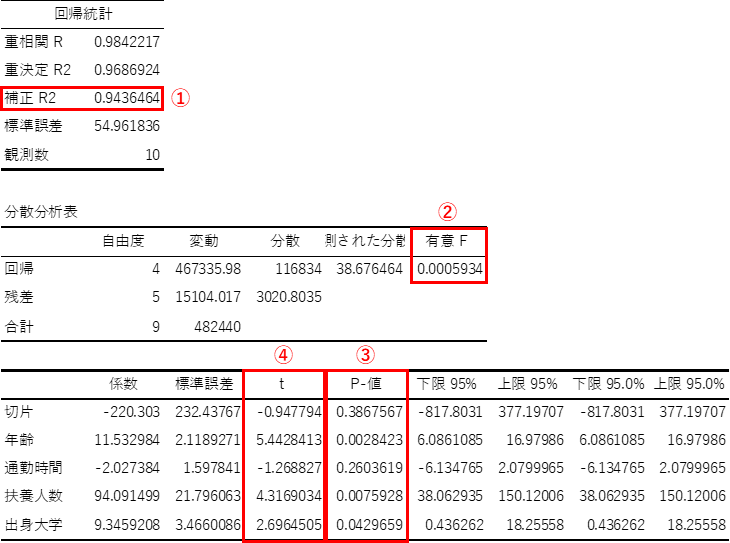
出力結果は,以下4つの観点で解釈することができます.
① 回帰式の当てはまりの良さ
重回帰分析で求めた回帰式がどの程度,説明変数で目的変数を予測できているかを確認します.この回帰式の精度を示す指標が「補正R2」になります.
「補正R2」とは,自由度調整済み決定係数のことで,この値が1に近いほど回帰式の精度が高いと判断できます.一般的な目安としては,0.8以上の場合に非常に精度が高いということできます.
例題では,0.943..と非常に精度の高い回帰式を求めることができたと言えます.
② 求めた回帰式の有意性
求めた回帰式が統計学的に意味があるかを確認します.「分散分析表」の「有意F」で調べることができます.
「有意F」はF検定統計量から得られるp値になります.p<0.05の場合,回帰式の説明力が高いのは偶然ではないと判断することができます.
例題では,p値が非常に小さい値のため求めた回帰式が統計学的に意味があると判断できます.
③ 偏回帰係数の有意性
偏回帰係数が目的変数に影響を与えているかを統計学的に判断します.各変数の「P-値」で調べることができます.
「P-値」は偏回帰係数に対して行うt検定のp値になります.ある説明変数がp<0.05の場合,目的変数の変動にその説明変数の影響があると統計学的に判断することができ,偏回帰係数に意味があると言えます.
例題では通勤時間がp\(\geq\)0.05であるため,年収に対して通勤時間は影響していないと言うことができます.その他の説明変数は,p<0.05であるため年収に影響があると言えます.
④ 説明変数の影響度
目的変数に対する説明変数の影響度を確認します.各変数の「t」で調べることができます.
「t」は偏回帰係数に対して行うt検定の検定統計量T値になります.T値の絶対値が大きいほど,目的変数に与える影響が大きいと言うことができます.
例題では,T値の絶対値は年齢が1番大きいため,年収に対して年齢の影響が最も大きいと判断することができます.
その他の出力項目や偏回帰係数のp値の考え方については,以下のページで解説しています.
説明変数の選択方法
重回帰分析の結果から,回帰式に含める説明変数の取捨選択を行うことでより精度の高い回帰式を求めることができます.
回帰式に含める説明変数の基準としては,偏回帰係数のp値が一般的には用いられます.p=0.1が基準となります.
説明変数の選択方法として2つ紹介します.
減少法
全ての変数を含めた状態から,基準に満たなくp値が最も高い変数を除く.
増加法
全ての説明変数のp値を求めてから,p値が最も低い変数を回帰式に含める.
いづれの方法でも,説明変数を選択するごとに重回帰分析を行い全ての変数が基準を満たした時点で完了となります.
ステップワイズ法とは,説明変数を1つずつ増やしたり削除することによって,良いモデルを探す方法です.良いモデルの規準としては,赤池情報量規準(AIC)やベイズ情報量規準(BIC)が用いられます.
ステップワイズ法は説明変数を逐次処理する方法の総称で,実際には説明変数の選択方法である減少法と増加法を組み合わせた,増減法を意味することが多いです.
重回帰分析の候補となる説明変数が多い場合に有効な手法で,統計解析アプリStaatAppではステップワイズ法を用いて,説明変数の自動選択を行うことができます.
→ StaatAppで行なう重回帰分析
回帰式を用いた予測
重回帰分析の目的の1つである,回帰式(予測式)を求め方を説明します.
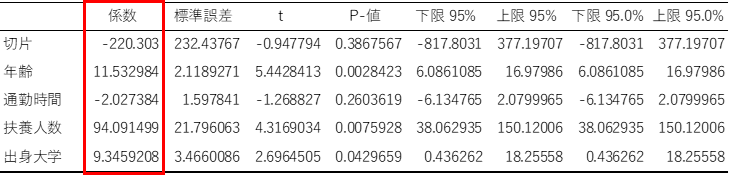
データ分析ツールで出力された3つ目の表の「係数」の列に着目します.「係数」は回帰式の偏回帰係数と切片になります.
例題では偏回帰係数と切片の値から,以下の回帰式を求めることができます.
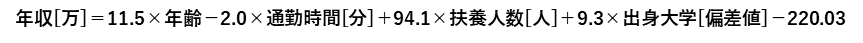
以下のような社会人のデータある場合,年収は回帰式に値を代入することで約614万と予測することができます.(予測精度は,,笑)

補足① 重回帰分析を行う前提条件
重回帰分析を行う際に用いるデータは,目的変数・説明変数ともに量的データである必要があります.
目的変数と説明変数がデータの種類よって用いる分析手法は異なります.それぞれの場合の分析手法については以下のページで解説しています.
説明変数にカテゴリーデータがある場合の対処法としては,一般化線形混合モデルを用いる方法とダミー変数を使う方法があります.一般化線形混合モデルはカテゴリーデータをランダム効果として,柔軟な分析が可能なのでおすすめです.ただし,分析の難易度はダミー変数を用いた重回帰分析の方が低いです.
目的変数が2値データ(Yes/No)の場合はロジスティック回帰分析を行なうことが多いです.
補足② 標準偏回帰係数
標準偏回帰係数とは全ての変数を標準化して,重回帰分析を行った際の偏回帰係数になります.
標準偏回帰係数を用いることで,単位の異なる説明変数間の偏回帰係数の大きさの比較を行うことができます.偏回帰係数の大きさは目的変数への影響度になるため,標準偏回帰係数を用いることで各説明変数の影響度の大きさを比較することができます.
説明変数を標準化しているだけなので,回帰式の当てはまりの良さや偏回帰係数のp値は元々の回帰式と一致します.目的変数の平均値が0になるので回帰式の切片は0になります.
補足③ 多重共線性(マルチコ)
多重共線性とは,説明変数同士に強い相関関係があることです.多重共線性があると分析結果で求めた説明変数の係数が不安定となり,解釈が難しくなるといった問題があります.
多重共線性を発見する方法としては,一般的にVIF(分散拡大要因)という指標が用いられます.VIFが大きい場合は該当する説明変数の除外・合成を行います.
補足④ 説明変数の適切な数
説明変数の数が適切でないと,分析結果に悪い影響を与えることがあります.
説明変数が少なすぎる場合,決定係数が0に近い値になり精度の低い回帰式になるといった問題が発生します.
逆に説明変数が多くなるほど,決定係数が1に近づき見た目の当てはまりの良さは上がります.しかし,あくまでの決定係数が1に近づいているだけであり,不必要な説明変数が入り込んでいる可能性が十分にあるので良い分析結果とはなりにくいです.説明変数の数はある程度絞る必要がありますが一般的な目安としては,説明変数の数は7個までとなります.ステップワイズ法でも紹介した,AICやBICといった情報量規準を用いて評価する場合もあります.
説明変数が多くなるほど決定係数が1に近づく問題については,分析結果の見方で説明した自由度調整済み決定係数を用いることである程度緩和されます.自由度調整済み決定係数は,自由度で割った係数であるので説明変数が多くなるほど値が小さくなります.例題でも,決定係数が0.968..で自由度調整済み決定係数が0.944..となっています.










