StaatAppで仮説検定を行う方法を紹介します．SaatAppではCSVファイルやExcelファイルを読み込み，クリック操作だけで，様々な仮説検定を行うことができます．
StaatAppについては以下をご覧ください．
アプリの基本操作
StaatApp基本操作（データの入出力など）は以下のページで解説しています．
対応のない場合の検定方法
対応のない場合の検定方法について解説します．対応のない場合とは，比較する標本（サンプル）を別の個体から得た場合のデータになります．
分析例として，社会人属性や収入などを示すデータから副業有無によって収入に差があるかを，マンホイットニーのU検定を用いて判定します．
帰無仮説は「副業有無によって収入に差がない」と設定して，対立仮説は「副業有無によって収入に差がある」となります．
分析で使用するサンプルデータは以下のようになります．
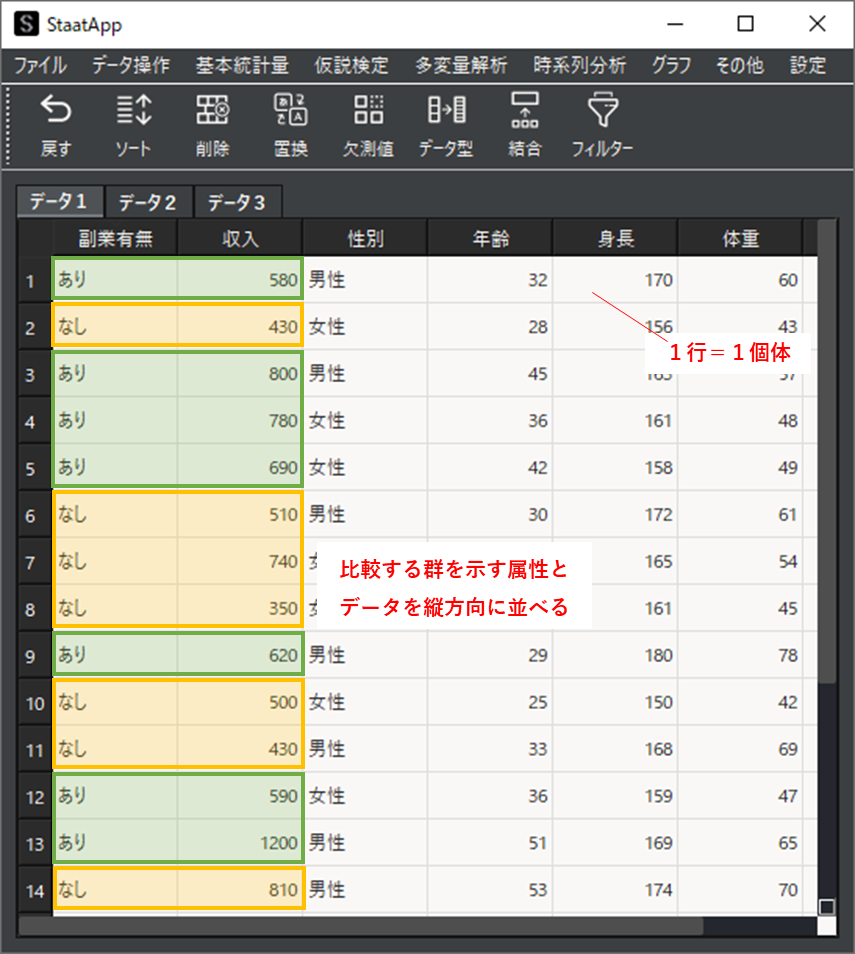
このような形式のデータをロングデータ（縦持ちデータ）と言います．ロングデータでは１行＝１個体のデータとして，所属する群（副業有無）を示す列と，比較対象のデータ（収入）が入力された列が必要です．
マンホイットニーのU検定を行うために，マンホイットニーのU検定用ウィンドウを表示します．
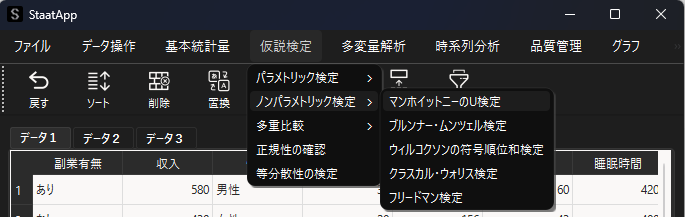
ウィンドウが表示されたら「変数選択」の「群名列」に”副業有無”を，「群A」に”あり”，「群B」に”なし”，「データ列」に”収入”を選択します．
「解析実行」ボタンをクリックすると解析結果が表示されます．
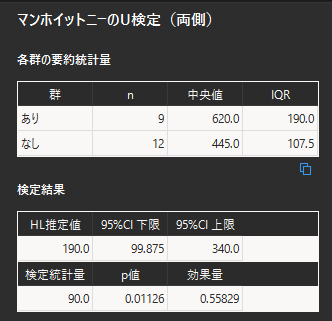
検定結果はp値＜0.05となるので，有意水準α＝0.05において「副業有無によって収入に差がある」ということがわかります．
ここまでが対応のない検定の１つであるマンホイットニーのU検定の実行方法になります．
片側検定を行う場合は，以下のように設定してください．
「群 A」が「群 B」より⼩さいことを調べたい場合 → 右側
「群 B」が「群 A」より⼩さいことを調べたい場合 → 左側
StaatAppでは対応のない場合の検定である一元配置分散分析や二元配置分散分析も，ロングデータ形式に対して実行することができます．
対応のある場合の検定方法
対応のある場合の検定方法について解説します．対応のある場合とは，比較する標本（サンプル）を同一の個体から得た場合のデータになります．
分析例として，学生のテストの得点示すデータから受験時期によって得点に差があるかを，フリードマン検定を用いて判定します．
帰無仮説は「受験時期によって得点に差がない」と設定して，対立仮説は「受験時期によって得点に差がある」となります．
分析で使用するサンプルデータは以下のようになります．
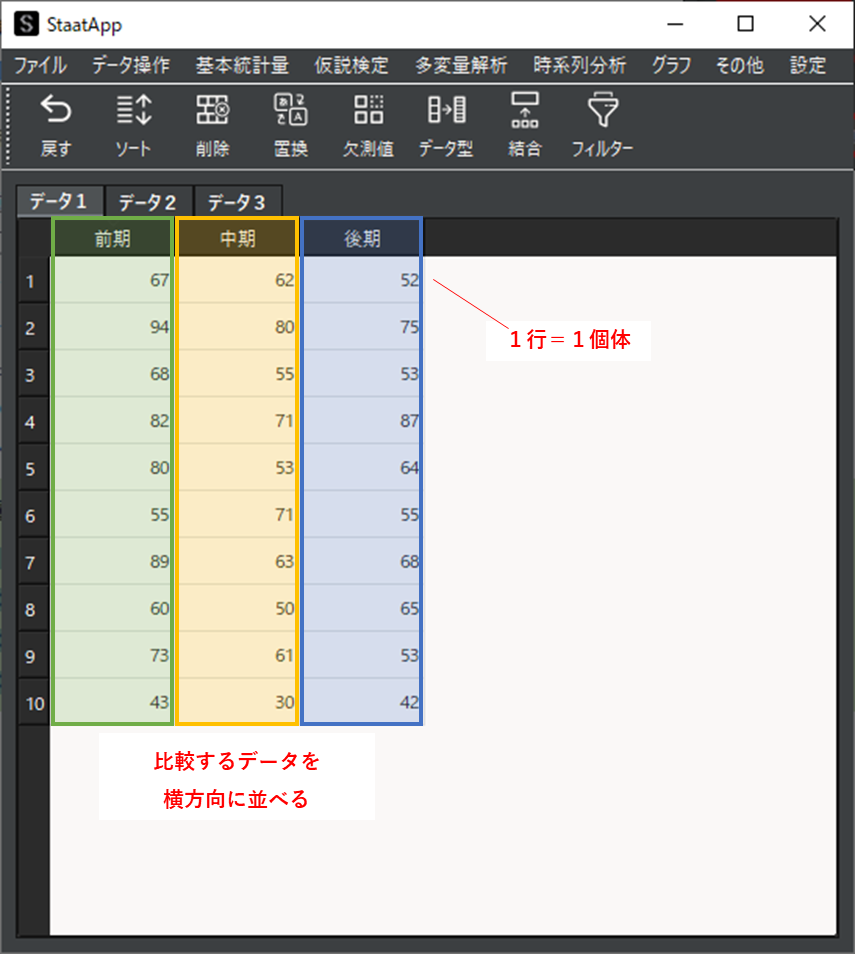
このようなデータ形式をワイドデータ（横持ちデータ）と言います．ワイドデータでは１行＝１個体のデータとして，比較対象のデータごとに入力された列が必要です．
フリードマン検定を行うために，フリードマン検定用ウィンドウを表示します．
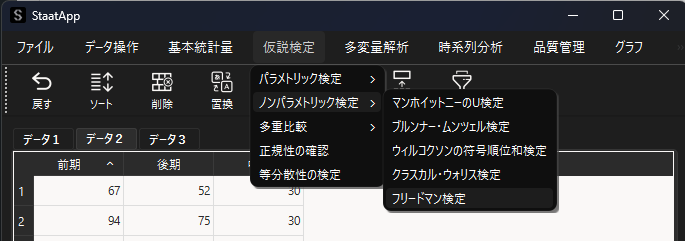
フリードマン検定用ウィンドウが表示されたら，「変数列選択」で検定対象のデータが入力された列を選択します．
「解析実行」ボタンをクリックすると解析結果が表示されます．
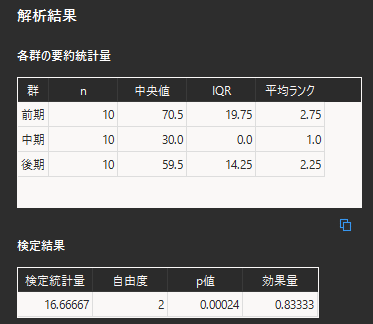
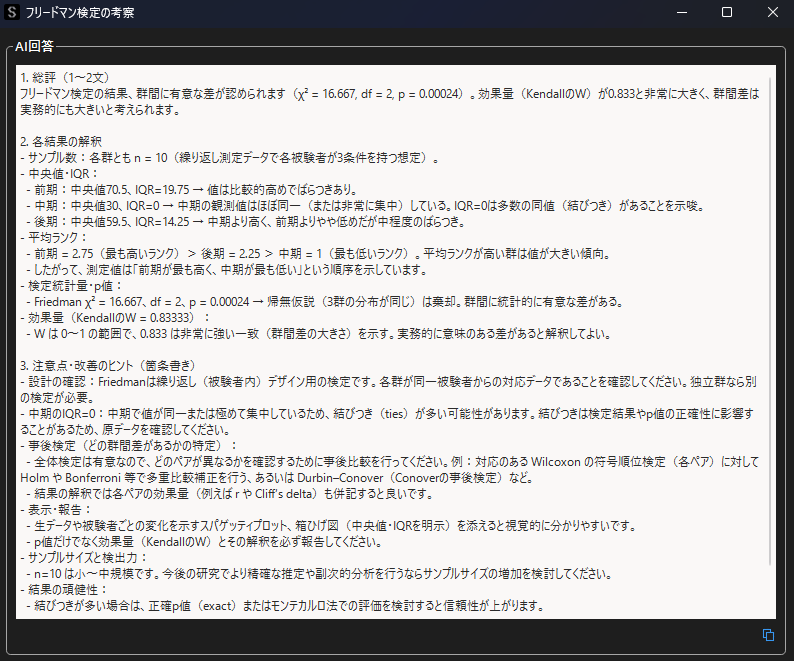
検定結果はp値＜0.05となるので，有意水準α＝0.05において「受験時期によってテストの得点に差がある」ということがわかります．
ここまでが対応のある検定の１つであるフリードマン検定の実行方法になります．
補足① 統計アプリStaatAppとは
StaatAppは計算仮定が複雑な解析手法を，誰でも手軽に素早く行なうことができるアプリです．本ページで紹介したマンホイットニーのU検定やフリードマン検定は有料版の機能となりますが，分散分析などのパラメトリック検定や，正規性の確認，データ操作機能は無料で利用いただけます．
StaatAppの詳細は以下のページをお読みください．
補足② 検定方法の選び方
検定対象のデータや目的によって，行うべき検定方法は異なります．検定方法の選び方については，以下のページで解説しています．
補足③ ロングデータ⇔ワイドデータの変換
StaatAppではロングデータ⇔ワイドデータの変換を，データ操作機能で行なうことができます．
StaatAppを用いたロングデータ→ワイドデータへの変換は以下のページで紹介しています．
