マクネマー検定とは
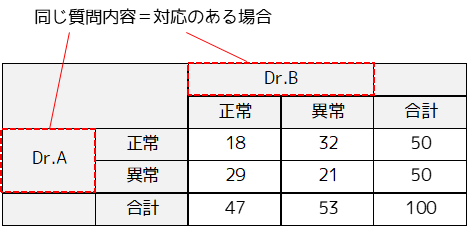
マクネマー検定とは対応のある場合の母比率の差の検定です.対応のある場合に,2つの群の母比率が等しいかどうかを判定するために行います.
➔ クロス集計表における対応のある・対応のない
検定統計量はカイ二乗分布に従います.以下の図がマクネマー検定の考え方になります.社会人70人に対する調査結果の例です.

マクネマー検定はクロス集計表に対して検定を行います.上記のようなクロス集計表の回答結果に差がある2つのセルから検定統計量を求めます.
検定統計量は2つのセルの値に差があるほど大きくなり,カイ二乗分布の限界値(上限)より大きい場合に標本の比率に差がある(母比率が異なる)と判定します.
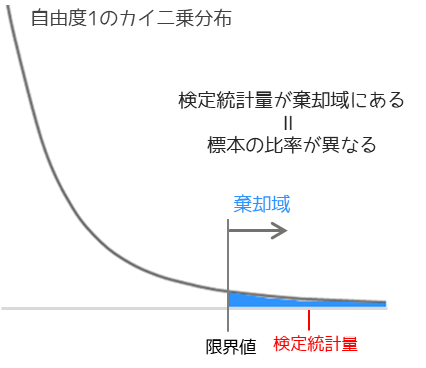
具体例では学生時代と現在の読書習慣に差があるといった結論になります.
マクネマー検定はどのような場面で用いるの?という方は補足をお読みください.
マクネマー検定の手順
マクネマー検定は以下の手順で行います.
① クロス集計表の作成
対応のある2×2クロス集計表を作成します.
② 仮説の設定
帰無仮説は「2標本の比率に差がない」,対立仮説は「2標本の比率に差がある」として設定します.
③ 有意水準の決定
有意水準α=0.05または0.01として設定します.一般的にはα=0.05で設定されます.
④ 検定統計量の算出
クロス集計表から検定統計量求めます.
⑤ p値の算出
検定統計量からp値を算出します.
⑥ 有意差判定
・p値<有意水準であれば,帰無仮説は棄却されて対立仮説を採択 → 「2標本の比率に差がある」
・p値\(\geq\)有意水準であれば,帰無仮説は棄却されない → 「2標本の比率に差があるとは言えない」
仮説検定の考え方や用語については,以下のページで解説しています.
例題で用いるデータと仮説の設定
例題では以下のサンプルデータを用います.社会人50人に対して学生時代と現在の読書習慣の調査をしました.1週間に30分以上読書をしていた,または現在している場合”はい”といった回答になっています.
| No. | 学生時代 | 社会人(現在) |
|---|---|---|
| 1 | はい | はい |
| 2 | いいえ | いいえ |
| 3 | いいえ | はい |
| 4 | いいえ | はい |
| 5 | いいえ | いいえ |
| 6 | いいえ | いいえ |
| 7 | いいえ | はい |
| 8 | いいえ | いいえ |
| 9 | いいえ | いいえ |
| 10 | いいえ | はい |
| 11 | いいえ | はい |
| 12 | いいえ | いいえ |
| 13 | はい | はい |
| 14 | いいえ | はい |
| 15 | いいえ | いいえ |
| 16 | はい | はい |
| 17 | はい | はい |
| 18 | はい | はい |
| 19 | いいえ | はい |
| 20 | いいえ | いいえ |
| 21 | いいえ | はい |
| 22 | はい | はい |
| 23 | はい | いいえ |
| 24 | いいえ | はい |
| 25 | はい | はい |
| 26 | いいえ | いいえ |
| 27 | はい | はい |
| 28 | いいえ | はい |
| 29 | いいえ | いいえ |
| 30 | はい | いいえ |
| 31 | いいえ | いいえ |
| 32 | はい | はい |
| 33 | はい | いいえ |
| 34 | いいえ | はい |
| 35 | いいえ | いいえ |
| 36 | いいえ | はい |
| 37 | はい | いいえ |
| 38 | はい | いいえ |
| 39 | はい | はい |
| 40 | いいえ | いいえ |
| 41 | いいえ | いいえ |
| 42 | いいえ | はい |
| 43 | いいえ | はい |
| 44 | はい | いいえ |
| 45 | はい | はい |
| 46 | いいえ | いいえ |
| 47 | いいえ | はい |
| 48 | はい | はい |
| 49 | いいえ | はい |
| 50 | いいえ | はい |
帰無仮説は「学生時代と現在で読書習慣に差がない」となり,対立仮説は「学生時代と現在で読書習慣に差がある」と設定します.
有意水準α=0.05で行います.
Excelを用いた計算手順
Excelを用いたp値の計算手順について説明します.
以下のような表を作成して,検定統計量とp値を求めます.
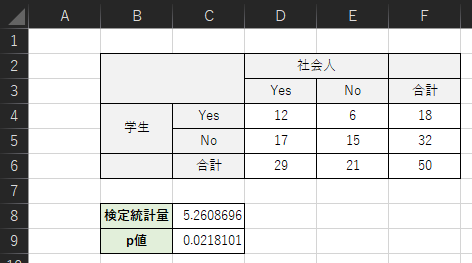
① クロス集計表を作成する
ローデータ(サンプルデータ)から2×2クロス集計表を作成します.Excelを用いたクロス集計表の作成方法についてはこちらのページで解説しています.
② 検定統計量を求める【C8】
クロス集計表のセルの値から検定統計量を求めます.検定統計量は以下の式で求めることができます.
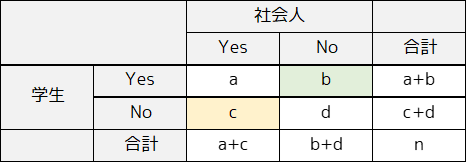

例題では5未満のセルがないので,以下の式で検定統計量を求めることができます.
ex) C8セルの入力式:=(E4-D5)^2/(E4+D5)
③ p値を求める【C9】
検定統計量からp値を求めます.検定統計量はカイ二乗分布に従うので,CHIDIST関数を用いてp値を求めることができます.
ex) C9の入力式:=CHIDIST(C8,1)
CHIDIST関数は引数として検定統計量と自由度を指定することp値を返します.2×2クロス集計表の自由度は1です.
例題ではp値は有意水準未満であるため帰無仮説は棄却され,「学生時代と現在で読書習慣に差がある」といった結論を得ることができます.
補足① 2標本の大小の比較
クロス集計表に対する仮説検定では,両側検定と片側検定の区別はありません.
仮説検定を用いて2標本の大小を判定したい場合は,標本間の割合を比較することで判断することができます.
例題では学生時代に比べて現在に読書習慣がある人の方が多いことが,クロス集計表から読み取れます.検定の結論として「学生時代より社会人の方が読書習慣がある」と言うことができます.
補足② マクネマー検定の使い方
マクネマー検定は母比率の差の検定の1つです.母比率の差の検定は,扱うデータが名義尺度である場合に行なうことがほとんどです.
母集団が正規分布に従うデータを扱う場合は,パラメトリック手法である対応のあるt検定など行ないます.
正規分布に従わない場合や順序尺度の場合は,ノンパラメトリック手法であるウィルコクソンの符号順位検定が可能です.
統計的仮説検定の選び方は以下のページで解説しています.
補足③ カイ二乗検定との違い
マクネマー検定と非常によく似た手法としてカイ二乗検定があります.
カイ二乗検定とは対応のない場合に行なうクロス集計表の分析手法です.統計学における対応のある・対応のないについては下記ページで解説しています.
以下のクロス集計表は大学生188人に対して1人暮らしの有無を調査した結果です.性別と1人暮らしの有無という項目でクロス集計を作成しました.

性別と1人暮らしという項目(表側と表頭)は関連性が全くありません.これがクロス集計表における対応のない場合です.
クロス集計表における対応のある場合とは,例題のようにクロス集計表の表側と表頭が時間経過や事象の発生前後における変化を示す項目,もしくは全く同じ項目で観測者が違う場合です.
後者の例としては,医療分野において同じ患者に対する2人の診断結果をクロス集計した場合があります.