ヒストグラム(度数分布図)とは
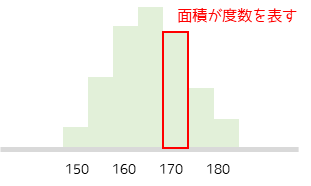
ヒストグラムとは数量データの分布を表すグラフになります.1つ1つの棒(ビン)の面積は階級ごとの度数を意味します.
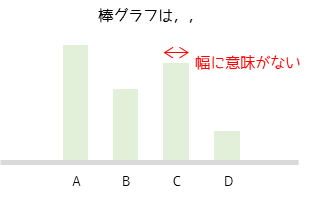
カテゴリーデータの度数を表す場合によく用いられる棒グラフとの違いは,棒の横幅に意味があるかどうかです.棒グラフは棒の高さのみで度数を表現するのに対して,ヒストグラムは面積で度数を表現します.
ヒストグラムの読み取り方
ヒストグラムは形状によって呼び名が定められており,形状から対象データの問題点などを読み取ることができます.形状ごとのヒストグラムの分類について紹介します.
一般型

一般型(山型)は中心部にかけて度数が大きくなり,両端に向かって左右対称に減少していく分布が特徴です.用いているデータが安定している,一貫性がある場合に多いです.
ふた山型

ふた山型は左右に2つの山があり,中央付近の度数が小さい分布になります.中央付近のデータが間違っている可能性や,複数の要因混ざっている可能性があります.
このようなデータ分布の場合,データに間違いがあるかの確認や,2つのデータに分割して原因を調査するといった対応が有効です.
歯抜け型

歯抜け型は区分ごとに度数がバラバラな分布になります.サンプルサイズが小さい場合や,区間の幅(ビン幅)が小さい可能性があります.
サンプルサイズを増やしてデータを取得する,またはビン幅を見直してヒストグラムを再作成するといった対応方法が有効です.
右裾引き型

右裾引き型は左端の度数が大きくなり,右端になるほど小さくなる分布です.集計したデータが一定以下の値を切り捨てられている可能性があります.
右裾引き型とは逆に右端が高く左端になるほど小さくなる場合は,一定以上の値が切り捨てられている可能性があります.
絶壁型

絶壁型は平均値が左右のどちらかに極端に偏り,片方の端の度数が大きい分布になります.データが意図的に選別されて,取り除かれている可能性があります.
データの収集方法や選択方法を見直すといった対応方法があります.
離れ小島型

離れ小島型はまとまった山型の分布から離れた位置にデータが存在する分布になります.離れた位置にあるデータは外れ値と呼ばれ,他のデータが混ざっている場合や測定ミスの可能性があります.
Excelを用いたヒストグラムの作り方
Excelを用いたヒストグラムの作り方を紹介します.Excelでは以下の3つの方法で,ヒストグラムを作成することができます.
① FREQUENCY関数で度数分布表を作成して,グラフ挿入機能の棒グラフを用いる方法.
② 「データ分析」ツールを用いる方法.
③ グラフ挿入機能のヒストグラムを用いる方法.
3つの方法の中で③が最も簡単で自由度が高いのでおすすめです.このページでも③の方法でヒストグラムを作成する手順を紹介します.※ 2013以前のバージョンでは実装されていません
作成例として,ある会社の従業員の年収分布をヒストグラムで表します.ヒストグラムに必要なデータを以下のように入力します.

データを入力したら,ヒストグラムに用いる値の範囲をドラッグして選択します.サンプルサイズが大きくてドラッグが難しい場合は,値の範囲の1番上のセルから「Ctrl + Shift + ↓」を押すことで一括選択が可能です.

データを選択した状態で,挿入タグのグラフからヒストグラムのようなアイコンを選択後,ヒストグラムを選択することで

デフォルトで以下のようなグラフが作成されます.
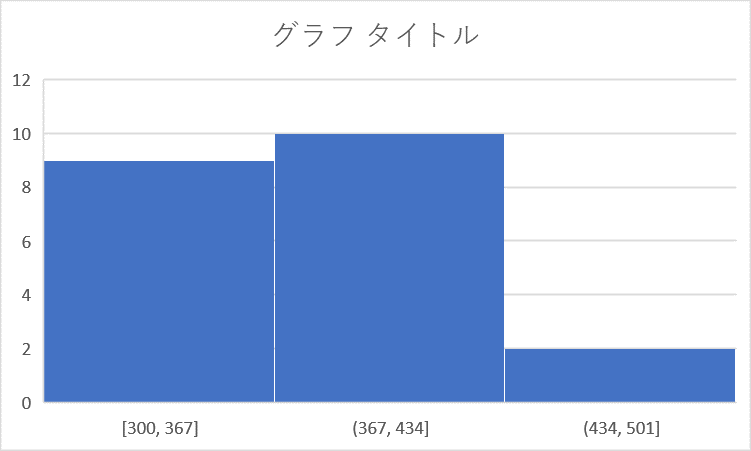
ヒストグラムの設定項目
Excelにおけるヒストグラムの設定項目について紹介します.
作成したヒストグラムの横軸ラベル選択した状態で右クリックを行い,「軸の書式設定」を選択することで画面右側に以下のようなウィンドウが表示され,設定を変更することができます.
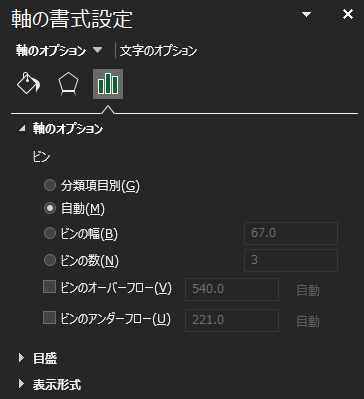
ビン(bin)とは棒のことを意味し,ヒストグラムにおいて1つの階級ごとの棒を意味します.ビンの設定を行うことで任意のヒストグラムを作成することが可能です.
設定項目は以下のようになります.
| 項目名 | 説明 |
| 自動 | ビンの幅・個数が自動で決まります. |
| ビンの幅 | 各階級の範囲を指定することでビン幅を定義できます. |
| ビンの数 | 指定した数のビンでヒストグラムが構成されます. |
| ビンのオーバーフロー | 階級の上限値を設定します.外れ値を除外する場合に用います. |
| ビンのアンダーフロー | 階級の下限値を設定します.外れ値を除外する場合に用います. |
※ 分類項目別は使用しません.
ヒストグラムはビン幅によって表現が大きく異なるため,どの幅に設定するかは非常に重要です.
以下のグラフは先程作成したグラフから,ビンの個数を10に変更したヒストグラムになります.
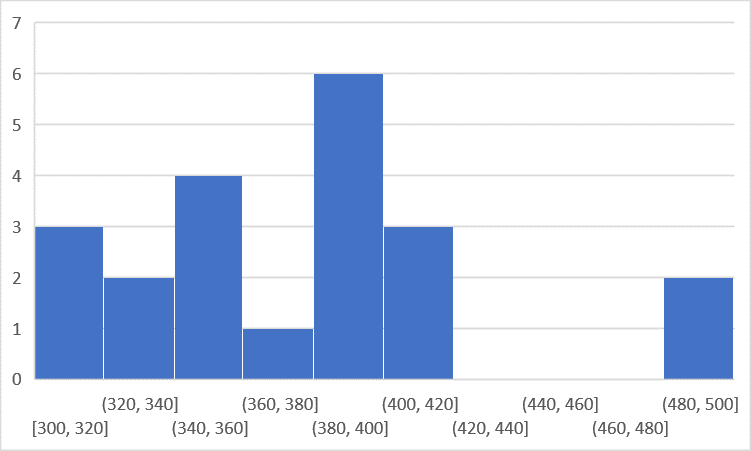
歯抜け型の分布をしているためサンプルサイズ小さい(n=21),もしくはサンプルサイズに対してビンの個数が小さすぎることがわかります.
ビン幅の決め方
ヒストグラムのビン幅(階級幅)の決め方にはいくつかの方法があります.ビン幅を直接計算する方法とビンの個数を計算する方法があります.ここでは4つの方法を紹介しますが,いずれも目安となるだけであり,正しいビン幅の決め方は存在しません.最終的にはどの幅の特徴に焦点を当てるかによって分析者が判断する必要があります.
以下で紹介する公式内で,hはビン幅,kはビンの個数,nはサンプルサイズを表します.
スコットの選択(Scott’s choice)
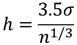
σはサンプルの標準偏差になります.
フリードマン・ダイアコニスの選択(Freedman–Diaconis’ choice)
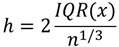
IQR(x)はサンプルxの四分位範囲を意味します.四分位範囲とは第3四分位値-第1四分位値で求めることができます.
平方根選択(Square-root choice)
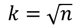
スタージェスの公式(Sturges’ formula)
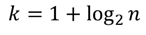
スタージェスの公式は最もよく使われる方法になります.サンプルサイズがある程度大きい場合(n>30)に有効です.
例題ではサンプルサイズが小さいので,スタージェスの公式は用いずにフリードマン・ダイアコニスの選択を用いてビン幅を計算します.Excelでの計算例は以下になります.
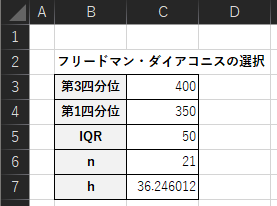
・C3セル:=QUARTILE(G3:G23,3)
・C4セル:=QUARTILE(G3:G23,1)
・C5セル:=C3-C4
・C6セル:=2*C5/C6^(1/3)
四分位値はQUARTILE関数で求めることができ,G3:G23はデータ範囲になります.計算結果からビン幅は36.24..となりました.
資料としてヒストグラムを用いる場合は,階級の区切りをある程度切りの良い値にすることも必要です.
StaatAppでヒストグラムを作成する
Excelでが2つのヒストグラムを同時に作成することはできません.2つのヒストグラムを同時に作成する場合は一般的にはRやPython,有料統計解析ソフトを用いて作成されます.
本サイトではStaatAppを用いた作成方法を紹介しています.StaatAppとは任意のデータをマウス操作だけで統計解析ができるPC用アプリです.RやPythonと比較しても簡単かつすぐにグラフ作成を行うことができます.
また,StaatAppではヒストグラム以外にも箱ひげ図やバイオリンプロットを作成することができます.
》StaatAppで作成するヒストグラム
》統計解析アプリStaatAppとは
グラフの選び方
統計解析においてグラフは様々な種類があります.分析対象のデータ・分析の目的に対して最適なグラフの選び方について,以下のページで解説しています.
参考文献と同じグラフが作成したい!けど,Excelでは難しい…
研究データを取りまとめて,論文執筆を行う際に以下の悩みはないでしょうか.
・参考文献と同じグラフを作成したいけど,Excelなどの表計算ソフトでは対応できない
・有料ソフト(SPSSなど)でも,参考文献と同じグラフを作成できない
・RやPythonで描画したいがプログラムの書き方がわからない
実際に既往研究と同じようなグラフを描画するためには,統計ソフトだけで対応することが難しく,RやPythonを用いたプログラミングが必要な場面が多々あります.
そこで本サイトでは,グラフ作成に関する代行,描画用プログラムの作成サービスを提供しております.本サービスではチャットで連絡を取りながらご希望のグラフを作成したり,お手元のデータで自由にグラフを描画できるプログラムの作成を行っています.









