コクランのQ検定とは
コクランのQ検定とは対応のある場合の3つ以上の2値変数に対する検定です.対応のある場合に,3群以上の変数間の割合に差があるかどうかを判定するために行います.→ 2値ではない場合
検定統計量はカイ二乗分布に従います.
以下の図がコクランのQ検定の考え方になります.社会人5人に対する調査結果の例です.
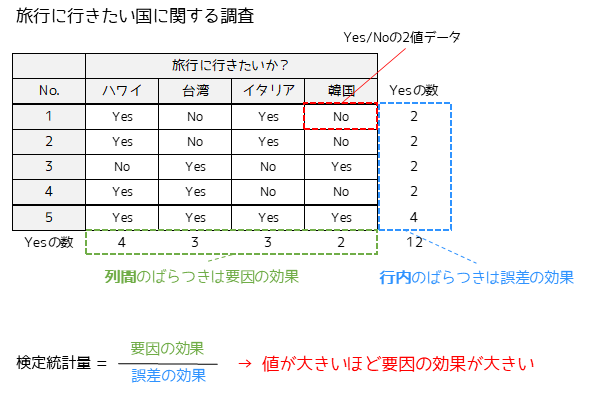
コクランのQ検定は整然データに対して検定を行います.上記のような整然データから各列・行の合計値(2値データを1/0に変換した合計値)を求めます.
各列の合計値の差は要因(国)による効果を示しており,各行間の合計値の差は誤差(回答者)による効果を示します.検定統計量は誤差の効果に対する要因の効果で求めることができます.
検定統計量は要因の効果が大きくなるほど値が大きくなり,カイ二乗分布の限界値(上限)より大きい場合に有意差があると判定します.
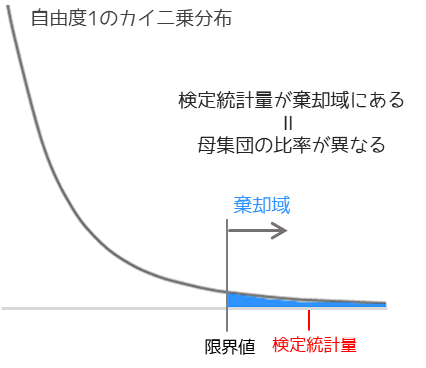
社会人5人に対する調査結果の例で有意差がある場合,「旅行に行きたい国に差がある」といった結論を得ることができます.
コクランのQ検定の手順
コクランのQ検定は以下の手順で行います.
① 仮説の設定
帰無仮説は「各群(各変数)の母集団の比率に差がない」,対立仮説は「各群(各変数)の母集団の比率に差がある」として設定します.
③ 有意水準の決定
有意水準α=0.05または0.01として設定します.一般的にはα=0.05で設定されます.
④ 検定統計量の算出
手元のデータから検定統計量求めます.
⑤ p値の算出
検定統計量からp値を算出します.
⑥ 有意差判定
・p値<有意水準であれば,帰無仮説は棄却されて対立仮説を採択 → 「各群の母集団の比率に差がある」
・p値\(\geq\)有意水準であれば,帰無仮説は棄却されない → 「各群の母集団の比率に差があるとは言えない」
仮説検定の考え方や用語については,以下のページで解説しています.
例題で用いるデータと仮説の設定
例題では以下のサンプルデータを用います.7人の社会人に対して行った,「4ヶ国のどこに旅行に行きたいか」という質問の回答結果になります.

帰無仮説は「4ヶ国の旅行人気に差がない」となり,対立仮説は「4ヶ国の旅行人気に差がある」と設定します.
有意水準α=0.05で行います.
Excelを用いた計算手順
Excelを用いたp値の計算手順について説明します.
以下のような表を作成して,検定統計量とp値を求めます.(説明のためハワイ→A,台湾→B,,,と変換しています)
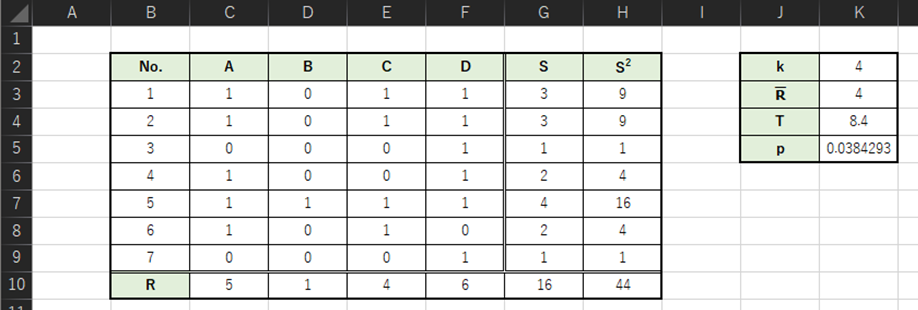
各セルの入力式は以下のようになります.
・C10:=SUM(C3:C9)
・G3:=SUM(C3:F3)
・G10:=SUM(G3:G9)
・H3:=G3^2
・H10:=SUM(H3:H9)
・K3:=(C10+D10+E10+F10)/K2
・K4:=(K2*(K2-1)*((C10-K3)^2+(D10-K3)^2+(E10-K3)^2+(F10-K3)^2))/((K2*G10)-H10)
・K5:=CHIDIST(K4,K2-1)
計算手順と入力式について説明します.
① 2値データを入力する
カテゴリーデータを”1”と”0”に変換した表を作成します.
② 各行の合計値と合計値の2乗を求める【G3-9】【H3-9】
作成した表の行ごとの合計値と,求めた合計値を2乗した値を求めます.
③ 各列の合計値を求める【C-H10】
②で求めた値の列ごとの合計値を求めます.
④ 各群の列合計値の平均値を求める【K3】
各群の列合計値の平均値を求めます.K2セルのkには群数(変数の数)を入力しておきます.
⑤ 検定統計量Tを求める【K4】
検定統計量Tを求めます.検定統計量は以下の式で求めることができます.
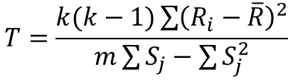
Riはi列の合計値,Sjはj行の合計値になります.
⑥ p値を求める【K5】
検定統計量からp値を求めます.ExcelではCHIDIST関数を用いてカイ二乗分布のp値を求めることができます.
CHIDIST関数の引数:CHIDIST(“検定統計量”,”自由度”)
自由度は群数-1で求めることができます.
例題ではp値は0.0384…となり有意水準未満であるため帰無仮説は棄却され,「4ヶ国の旅行人気に差がある」といった結論を得ることができます.
補足① データの前提条件
コクランのQ検定を行う際の扱うデータの前提条件について紹介します.
① 対応のある場合
コクランのQ検定は対応のないグループ(別個体)のデータに対しては用いることができません.対応のない場合は,独立性の検定を行う必要があります.
② 3群以上の場合
コクランのQ検定は3群以上の差の検定になります.2群の差の比較を行なう場合は,マクネマー検定を行います.
③ 2値データ(質的変数)
2値データに対して行います.3値以上の順位データなどに対して比較を行なう場合は,フリードマン検定を行います.扱うデータが量的データである場合は,対応のある一元配置分散分析を行います.
補足② 多重比較との関係性
コクランのQ検定では,3つ以上グループがある場合にどのグループとどのグループが異なるかまでは判断することができません.これらのことを判断したい場合は,「多重比較」という分析を行います.









