テューキー法(Tukey法)とは
テューキー法は対応のないt検定を,3群以上の標本に対して使えるようにした検定方法です.
検出力が高いため,多重比較の中で最も一般的な手法になります.比較方法としては,全ての2群同士を平均の差が大きいか否かで判断します.
以下の図がテューキー法の考え方になります.
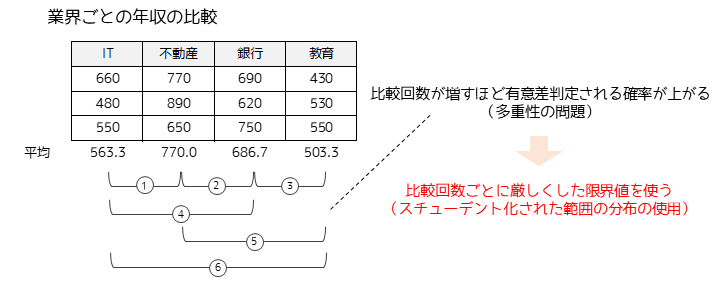
4群に対して2群の平均の差の比較を行なう場合,検定回数は6回必要になります.有意水準α=0.05で検定を6回繰り返すと有意になる確率は26%(=1-(1-0.05)6)に上昇します(多重性の問題).
多重性の問題を解決するためにテューキー法では,比較する群数が増えるごとに厳しくした限界値を用いて仮説検定を行います.
似た手法としてテューキー・クレーマー法(Tukey-Kramer法)がありますが, テューキー・クレーマー法は比較するグループのサンプルサイズ(データ数)が一致していない場合にも検定を行うことが可能です.
テューキー法の手順
テューキー法は以下の手順で行います.テューキー・クレーマー法も同様の手順です.
① 仮説の設定
帰無仮説は「各群間の母平均に差がない」,対立仮説は「各群間の母平均に差がある」として設定します.
② 有意水準の決定
有意水準α=0.05または0.01とします.一般的には0.05で設定されます.テューキー法は両側検定のみとなります.
③ 検定統計量の算出
具体的な計算手順は,Excelを用いた方法で解説しています.
④ 有意差判定
限界値<検定統計量であれば,帰無仮説は棄却されて対立仮説を採択 → 「比較した2群の母平均に差がある」
限界値\(\geq\)検定統計量であれば,帰無仮説は棄却されない → 「比較した2群の母平均に差があるとは言えない」
仮説検定の考え方や用語については,以下のページで解説しています.
検定結果を間違いたくない方へ
Excelを用いた計算方法より簡単・正確に,テューキー・クレーマー法の検定結果を調べることができる統計解析アプリStaatAppを販売しております.
StaatAppではテューキー・クレーマー法以外にも様々な仮説検定・多重比較をクリックするだけで実行することができます.詳細は以下のページをお読みください.
》StaatAppで行う仮説検定
》統計解析アプリStaatApp
例題で用いるデータと仮説の設定
例題では以下のサンプルデータを用います.4つの業界で働いている社会人に対して年収を調査した結果になります.

帰無仮説は「各業界ごとに年収の差はない」となり,対立仮説は「比較した業界間で年収に差がある」と設定します.
有意水準α=0.05で検定は行います.
Excelを用いた計算手順
Excelを用いた検定統計量の計算手順について説明します.
以下のような表を作成して,検定統計量qを求めます.
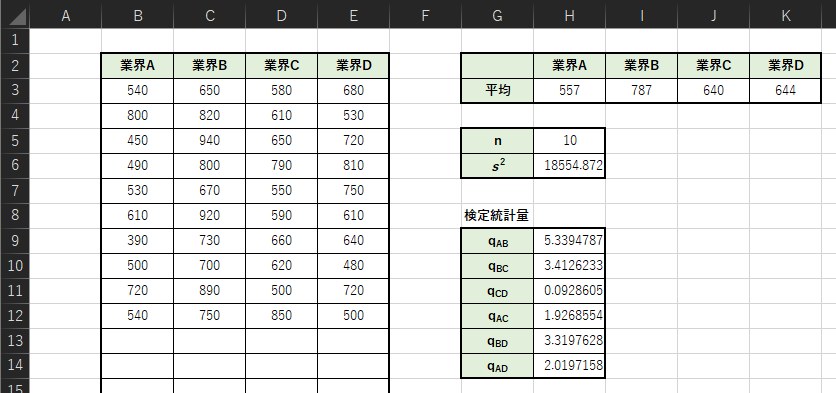
各セルの入力式は以下のようになります.
・H3:=AVERAGE(B3:B12)
・H6:=VAR.S(B3:E12)
・H9:=ABS(H3-I3)/SQRT(H6/H5)
計算手順と用いた関数について説明します.
① 各群の平均を求める【H-K3】
各群の平均を計算します.AVERAGE関数を用いて平均値を計算することができます.
② サンプルサイズを求める【H5】
サンプルサイズを入力します.
③ 不偏分散を求める【H6】
標本全体の不偏分散を求めます.VAR.S関数を用いることで不偏分散を求めることができます.
④ 検定統計量を求める【H9-14】
比較する群間の検定統計量を計算します.検定統計量は以下の式で求めることができます.
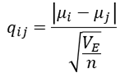
i,jは比較するグループ,\(\mu\)は各群の平均値,VEは不偏分散,nはサンプルサイズです.Excelでは絶対値と平方根はABS関数とSQRT関数用います.
有意差判定の手順
検定統計量を用いた有意差判定について解説します.
① 比較する順序の決定
2つの群ごとに比較を行なうために,比較する順番を決めます.比較する順番は各群の平均値の大小関係で決めることができます.
例えば,4つのグループの平均値の大小関係が,A > B > C > Dとすると最も平均の差が大きいAとDの比較を最初に行います.ここで有意差が見られない場合,その他のグループ間ではより平均値の差が小さいため,有意差が見られないといった結論を得ることができます.
有意差が見られた場合は,次に最大平均であるAと2番目に平均値が小さいCの比較を行います.ここでも有意差が見られた場合は,AとBの比較さらには2番目に大きい平均値のBとDの比較といった順序で行います.
例題では,求めた平均値の関係から業界Aと業界B,業界Bと業界C,業界Bと業界D,業界Aと業界D…の順序で比較を行います.
② 検定統計量と検定表から有意差の判定をする
Excelでの計算手順で求めた検定統計量と,スチューデント化された範囲の分布を用いて有意差を判定します.
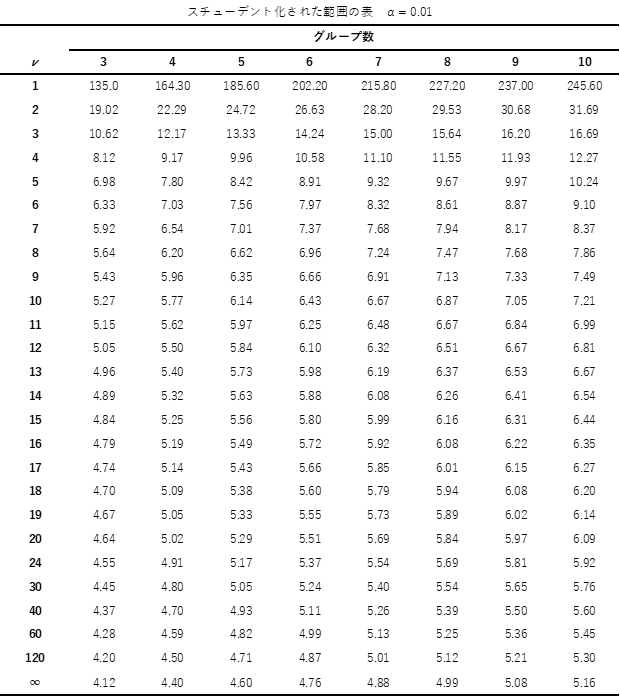
スチューデント化された範囲の分布の見方は,行が自由度で列が群数になります.自由度は「総データ数ー群数」で求めることができます.
例題では自由度は40-4=36となります.群数は4となるので, 有意水準α=0.05における限界値は3.79から3.85の間となります.
業界Aと業界Bを比較した検定統計量は5.339..であったので, 検定統計量>限界値となり有意差があると判定できます.結論としては,対立仮説の「業界Aと業界Bの社会人には年収の差がある」となります.
③ その他の群間の比較を繰り返す
比較する群ごとに②を繰り返し行い,有意差の判定をします.
例題では,その他の群間の検定統計量は限界値以下となりました.結論としては,「業界Aと業界B以外の業界間に年収の差があるとは言えない」となります.
補足① スチューデント化された範囲の分布
テューキー法の検定表として用いる,スチューデント化された範囲については以下の通りになります.
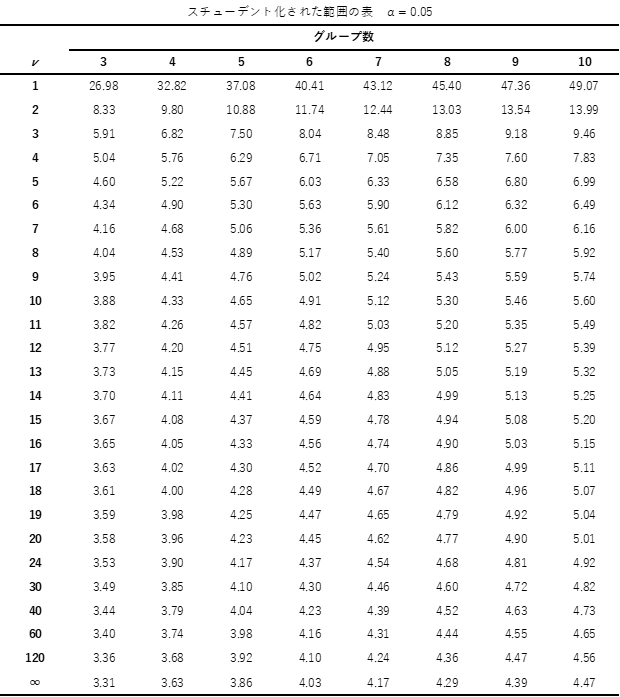
補足② テューキー・クレーマー法の検定方法
比較する群間でサンプルサイズが異なる場合は,テューキー法ではなくテューキー・クレーマー法を行います.計算手順は基本的にはテューキー法と同じです.
異なるのは検定統計量を求める計算式になります.テューキー・クレーマー法で用いる式は以下のようになります.i,jは比較するグループを示しています.
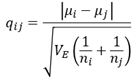
サンプルサイズが同じだった場合にこの式を用いると,テューキー法での検定統計量を\(\sqrt 2\)で割った値と同じ値を求められることがわかります.
Excelでの計算方法としては,テューキー法で説明した検定統計量を求める式の分母を上記に式に合うように修正するだけです.
限界値はスチューデント化された範囲の分布から読み取った値を\(\sqrt 2\)で割った値となります.
補足③ 限界値の補完方法
スチューデント化された範囲の分布には記載されていない自由度の検定統計量を求める方法について説明します.
例題のように有意水準α=0.05で自由度が36であった場合について,前後の自由度をそれぞれa,bとします(a=30, b=40).前後の自由度の限界値をそれぞれqa,qbとします(qa=3.85,qb=3.79).
限界値は以下の式で求めることができます.
限界値=式1+式2
式1=(1/m-1/b)/(1/a-1/b)×qa
式2=(1/a-1/m)/(1/a-1/b)×qb
m=36(求めたい自由度)とした場合,限界値は3.81となります.
補足④ 効果量について
仮説検定の結果として重要な効果量の求め方について紹介します.
多重比較では比較した2群ごとに効果量を計算する必要があります.効果量は様々な方法で計算することができますが,2群の平均の差の効果量で一般的に使われるのはCohen’s dになります.
Statistical Power Analysis for the Behavioral Sciences by Jacob Cohen (1988)
Cohen’s dは以下の式で求めることができます.
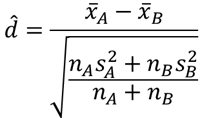
xA,xBは各グループの平均,nA,nBはサンプルサイズ,sA,sBは標本標準偏差になります.Excelを用いた計算方法は以下のページの補足事項として紹介しています.
補足⑤ 検定の前提条件
3つ以上のデータの差の比較を行う多重比較には様々な手法があります.多重比較の1つであるテューキー法を行う際に,用いるデータの満たすべき条件について説明します.
① 対応のないデータ
比較する2つのグループは対応のない場合である(異なる個体のデータ)である必要があります.対応のある場合は,パラメトリック検定である反復測定分散分析やノンパラメトリック検定のFriedman(フリードマン)検定があります.
② パラメトリックなデータ
テューキー法はパラメトリックな(=正規分布と仮定できる)データに対して行います.用いるデータが正規分布と仮定できない場合は,スティール・ドゥワス検定などがあります. この手法は,テューキー法のノンパラメトリック版の検定方法になります.
》正規性の調べ方
》ノンパラメトリック検定
》スティール・ドゥワス検定
③ 等分散性のあるデータ
比較するグループの母分散が等しい必要があります.等分散性が無いデータの場合は,Bonferoni法(ボンフェロー二補正)を用いて多重比較を行います.










