評価指標の基本(混合行列)
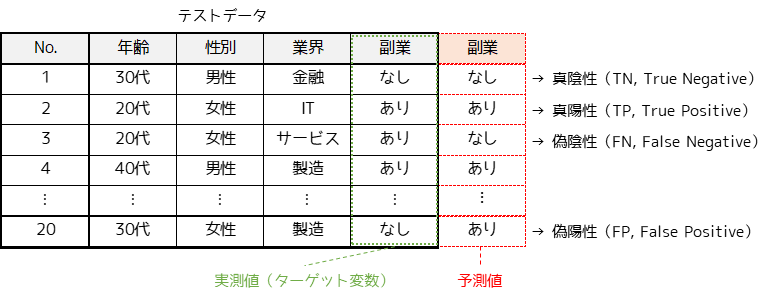
機械学習における分類問題ではテストデータを用いて,モデル(学習結果)の予測値とテストデータの値(実測値)を比較することで,モデルの精度評価を行います.
実測値と予測値の判定結果には4つのパターンがあり,それぞれ以下のように表現されます.
・真陽性(TP, True Positive):実測値が○で,予測値も○
・真陰性(TN, True Negative):実測値が×で,予測値も×
・偽陽性(FP, False Positive):実測値が×で,予測値が○
・偽陰性(FN, False Negative):実測値が○で,予測値が×
実測値と予測値をクロス集計した表を,混合行列と言い以下のようになります.
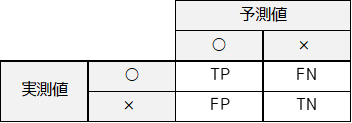
分類問題の評価指標ではこの4パターンを用いて,様々な値が利用されます.
様々な評価指標
正確度・正解率(accuracy)
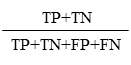
正確度は全データに対する予測値が的中した割合になります.最もわかりやすい指標なので,よく用いられます.
ただし,ターゲット変数に偏りがありほどんどが○の場合,全ての予測値を○とすれば正確度は高くなるというデメリットがあります.つまり,ターゲット変数の中の稀な値を判定する場合の評価指標としては不向きになります.
このあと説明する多クラス分類問題でも,適切な指標値となります.
適合率(precision)
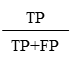
適合率は予測値が○であるデータのうち,実測値が○であったデータの割合です.適合率は誤って○と判定すると,損失が大きい場合によく用いられます.
例えば,スパムメールの検出では,正規のメールをスパムと誤って分類すると非常に問題となるため,適合率が重要な指標となります.
再現率(recall)
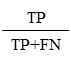
再現率は実測値が○であるデータのうち,○と予測できたデータの割合です.再現率は○であることを逃すと損失が大きい場合によく用いられます.
例えば,病気の診断テストでは,実際には病気の人を健康と誤診することが避けられなければならないため,再現率が重視されます.
F値(F-valus)
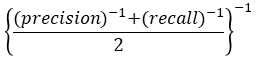
F値は適合率と再現率の調和平均で算出されます.適合率と再現率はトレードオフの関係にあるため,バランスの取れたよいモデルを評価するために用いられます.
例えば,情報抽出や検索エンジンのランキングアルゴリズムなどで使用されます.
その他の評価指標
その他にも以下のような評価指標があります.
| 名称 | 定義 | 概要 |
| 陰性適中率(NPV, Negative Predictive Value) | TN/(TN+FN) | 予測値は×のうち,実測値が×である割合 |
| 偽陽性率(FPR, False Positive Rate) | FP/(FP+TN) | 実測値が×のうち,予測値が○である割合 |
| 真陰性率,特異度(TNR, True Negative Rate) | TN/(FP+TN) | 実測値が×のうち,予測値が×である割合 |
| 偽陰性率(FNR, False Negative Rate) | FN/(TP+FN) | 実測値が○のうち,予測値が×である割合 |
ROC曲線(Receiver Operating Characteristics Curve)
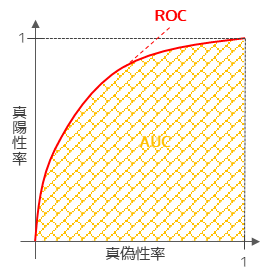
ROC曲線は縦軸に真陽性率(再現率),横軸に偽陽性率を取ってプロットした曲線になります.縦軸と横軸に囲まれた正方形の面積1に対して,ROC曲線と横軸で囲まれた面積の割合をAUCと言います.
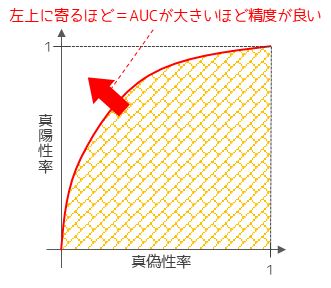
ROC曲線は左上に寄るほど,つまりAUCが大きいほどモデルの予測精度が高いこと意味します.逆にROC曲線が直線の場合,AUCが最小値の0.5の場合,モデルは完全にランダムで分類を行っていることを意味します.
多クラス分類の場合
ここまでの指標値は○か×という,二値分類問題に対する考え方になります.”副業”という変数はカテゴリーが”あり” or “なし”であったため二値分類問題でした.
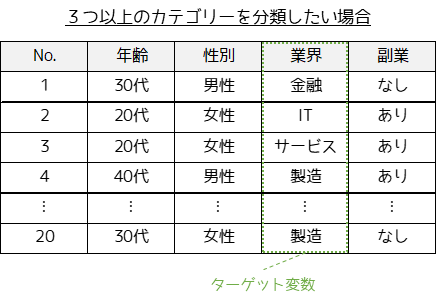
ターゲット変数を”業界”とした場合,”金融”・”IT”・”サービス”・”副業”の4つのカテゴリーがあるため,多クラス分類問題となります.
多クラス分類問題では,クラスごとに指標を計算します.
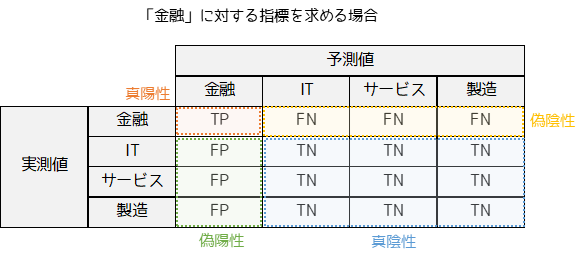
例えば”金融”に対して評価指標を考える場合,上記のような混合行列となります.
適合率や再現率は全てのクラスに対して集計して評価する場合もあります.全てのクラスに対する指標値を集計する方法としては以下のような方法があります.
マクロ平均
各クラスについて計算した指標の算術平均を取ります.これはすべてのクラスを等しく扱うため,クラスの不均衡に対して敏感です.
マイクロ平均
全体の混同行列を作り,全体を通じての指標値を計算します。これは各クラスのサンプル数に応じて重み付けを行うため,各クラスのサンプル数に偏りがある場合,サンプル数の大きいクラスの評価指標の影響度が大きくなります.
重み付け平均
各クラスの指標にそのクラスの重み付けを行い,平均値を算出します.
機械学習を行うならStaatApp
統計解析アプリStaatAppでは機械学習の代表的な手法である決定木を,プログラミングを行わずクリック操作だけで扱うことができます.発展的な手法であるランダムフォレストや勾配ブースティング決定木にも対応してます.
決定木機能については無料版で利用できますので,以下のサイトよりダウンロードしてお使いください.
》統計解析アプリStaatApp
》Staatappを用いた決定木










