t検定や分散分析などのパラメトリック検定を行うための前提条件である,「母集団が正規分布に従う(正規性がある)」を調べる方法について解説します.
正規性の調べ方
データの正規性を調べる方法としては,グラフを用いる方法と仮説検定の2つがあります.
グラフを用いる方法では主にヒストグラムやQ-Qプロット(Quantile-Quantile Plot)を作成してデータの分布を視覚化することで正規分布に従うか判断します.
仮説検定では主にシャピロ・ウィルク検定やコルゴモロフ・スミルノフ検定が使われます.仮説検定では「データの母集団の分布は正規分布に従う」という帰無仮説を設定して,有意差がある場合に正規性がないと判断します.
どちらの方法もメリット・デメリットがあり,正規性の調べ方に最適な手法・判断基準はないのが現状です.実際にパラメトリック検定が実施可能かを判断する場合は,中心極限定理を活用することをおすすめします.
グラフを用いた調べ方
グラフを用いる方法では,仮説検定と比較して比較的簡単に正規性を調べることができます.特にヒストグラムは統計学の基本的なグラフであり,Excelでも簡単に作成することができます.
グラフを用いる場合に留意するべきこととして,視覚的に判断を行うため正規性の判定がデータ分析者の主観によってしまうという点です.どのような形であれば正規性があると判定できるといった厳密な基準はありません.
① ヒストグラム
ヒストグラムとは量的データの分布を表すグラフになります.1つ1つの棒(ビン)の面積は階級ごとの度数を意味します.
正規性がある場合,正規性ない場合のヒストグラムの形は以下のようになります.
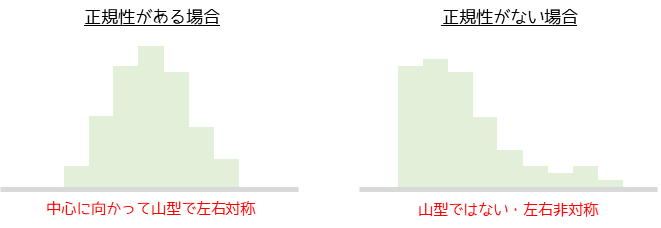
正規性がある場合はヒストグラムは左右対称な山型となります.逆に左右対称の山型ではない場合は,データが正規分布に従わないと判断することができます.
ヒストグラムは設定したビン幅よって見え方が変化する点に注意が必要です.
② Q-Qプロット
Q-Qプロットは2つの分布を比較する場合に用いられるグラフになります.比較した2つの分布が等しい場合,プロットが一直線に分布します.
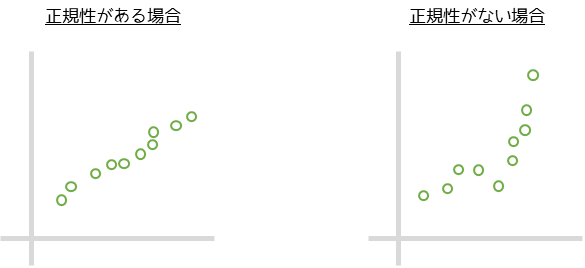
正規性を調べる場合は,データと正規分布を比較してQ-Qプロットが直線に並んだ場合にデータが正規分布に従うと判断します.
仮説検定を用いた調べ方
仮説検定では以下のように帰無仮説と対立仮説を設定します.
・帰無仮説:データの母集団が正規分布に従う
・対立仮説:データの母集団が正規分布に従わない
検定の結果,p値\(\geq\)0.05の場合に正規性があり,p値<0.05の場合に正規性がないと判断することが多いです.ただし仮説検定で正規性を調べる場合は,以下の2点に留意する必要があります.
・有意差がない場合に,積極的に正規性があると主張することができない
➔ 仮説検定の考え方
・多重性の問題が起きる
➔ 多重性の問題(多重比較)
① シャピロ・ウィルク検定
シャピロ・ウィルク検定はデータに正規性があるかを調べる検定手法です.コルゴモロフ・スミルノフ検定と比較してサンプルサイズが小さい場合に,厳しい判定となります(有意差が出やすい).
ここで言う”サンプルサイズが小さい”の明確な基準はありませんが,n=200以下の場合でシャピロ・ウィルク検定の方が有意差が出やすいといった実験結果があります.
② コルゴモロフ・スミルノフ検定
コルゴモロフ・スミルノフ検定は分布一般の比較に用いられる検定方法です.特に1標本のコルゴモロフ・スミルノフ検定では,データ(標本)と正規分布を比較することでデータの正規性を調べることができます.
補足① 実際に調べてみる
ここまで紹介した手法はヒストグラム以外,手計算やExcelを用いて行うことは難しいです.一般的にはRやPython,有料統計解析ソフトを用いて行われます.
本サイトでは2つの方法を紹介しています.
① Pythonを用いた方法
Pythonを用いた方法に初めてプログラミングを行う方でもわかるように解説しています.
》Pythonを用いた統計解析
》Pythonを用いた正規性の調べ方
② 統計解析アプリ(StaatApp)を用いた方法
StaatAppとは任意のデータを数クリックだけで統計解析ができるPC用アプリです.Rと比較しても簡単に分析を行うことができるので,今すぐ結果を知りたい方におすすめです.
本ページで紹介した正規性の確認方法は,全て無料版StaatAppで実行可能です.無料版StaatAppについては以下のページで紹介しています.
》無料版StaatAppの使い方
》統計解析アプリStaatApp
補足② 正規性の判定が難しい場合
実績のデータ分析では,きれいに正規分布に従うデータを扱うことの方が珍しくなります.ヒストグラムを作成してみてこのデータが正規分布に従うか判断しかねる場面も多々あります.
正規性の判定が難しい場合は,正規性の必要ないノンパラメトリック検定を用いる方が統計学的な誤りを犯す可能性は極めて低くなります.t検定と代表的なノンパラメトリック検定の1つであるマンホイットニーのU検定の検定力は5%程度しか変わりません.
逆に扱うデータが確実に正規分布に従うと判断できる場合や中心極限定理を活用できる場合のみ,パラメトリック検定を行うことをおすすめします.










