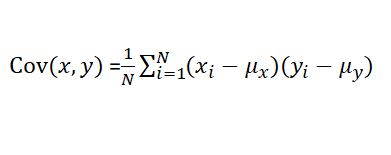共分散をPythonを用いて簡単に求める方法を紹介します.
共分散とは
共分散とは,2つの連続型の変数の関係性を見るときに用いる統計量です.
変数xと変数yを持つデータがあった際に,共分散で示される関係性は以下のようになります.
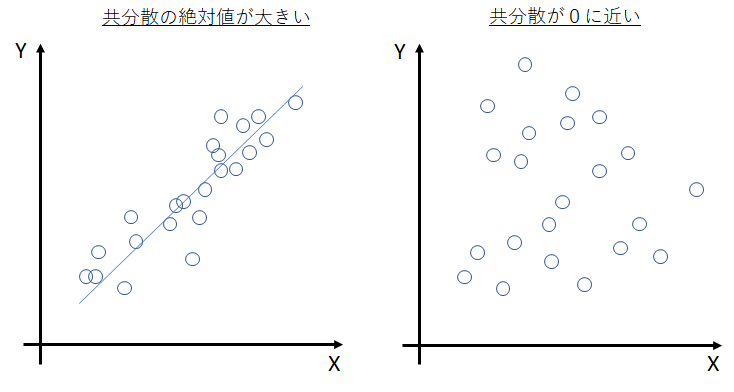
共分散の絶対値が大きいと,xが増加するに従ってyは増加または減少する傾向が強くなります.
一方で,共分散が0に近い(絶対値が小さい)と右図のようにばらばらな分布になり関係性が見られなくなります.
Scipyを用いた共分散の求め方
Scipyには,分散共分散行列を求めるcov関数があります.
分散共分散行列とは,以下の式のように2変数の分散と共分散を示して行列です.
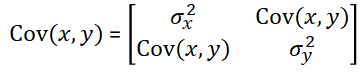
Covが変数x,yの共分散(covariance)を示しています.
実際に分散共分散を求めてみます.
# ライブラリのインポート
import pandas as pd
import scipy as sp
# データの読み込み
city_info = pd.read_csv("city.csv")
print(city_info)
Class Population Area
A town 10 50
B town 15 40
C city 30 80
D city 20 100
E city 50 70
F town 10 10
# データの取り出し
x = city_info["Population"]
y = city_info["Area"]
# 分散共分散行列を求める
print(sp.cov(x, y, ddof=0))
[[197.91666667 204.16666667]
[204.16666667 847.22222222]]PopulationとAreaの分散共分散行列を求めました.
PopulationとAreaの共分散は204.166となります.
因みに,共分散の公式は下記のようになりますが1/(N-1)とする場合はddof=1とします.